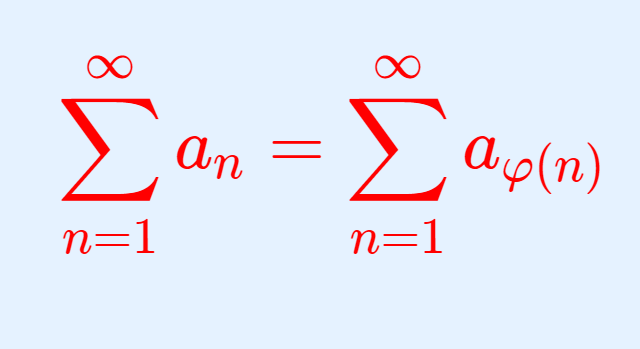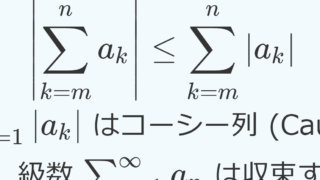有限和のときは， a_1 +a_2+ a_3 = a_3 + a_1 + a_2 のように，和の順序を入れ替えても値は同じになりますが，無限和のときは，一般にそうとは限りません。
しかし，絶対収束級数においては，項の順番を任意に入れ替えても，同じ値に収束することが知られています。この定理を紹介し，証明しましょう。
定理の主張～絶対収束なら和の順序によらず同じ値に収束～
定理
数列 \{a_n\} の和が絶対収束，すなわち \sum_{n=1}^\infty |a_n| < \infty をみたすとする。
このとき，数列 \{a_n\} と，正の整数の間の任意の全単射 \varphi\colon \mathbb{Z}_{\ge 1} \to \mathbb{Z}_{\ge 1} によって項の順番を変えた数列 \{a_{\varphi(n)}\} の和は同じ値に収束する。すなわち，
となる。
この定理は実数列でも複素数列でも成立します。
なお，絶対収束級数は， \sum_{n=1}^\infty a_n も収束することが知られていますが，これが分からない場合は，以下の記事を参照してください。
証明
まず比較的簡単な正項級数，すなわち a_n \ge 0 \,\,(n\ge 1 ) の場合に証明したいと思います。それから，それとは別に，一般の実数または複素数の絶対収束級数の場合の証明をしたいと思います。
正項級数の場合
証明
L = \sum_{n=1}^\infty a_n とおく。 n \ge 1 に対し，
M_n = \max_{1\le k \le n} \varphi(k)と定めると， a_n \ge 0 より，
\sum_{k=1}^n a_{\varphi(k)} \le \sum_{k=1}^{M_n} a_k \le Lであり，特に n\to \infty とすることで，
\sum_{k=1}^\infty a_{\varphi(k)} \le Lとなる（正項級数のため，左辺の極限が存在することに注意）。
すなわち，
\sum_{n=1}^\infty a_{\varphi(n)} \le \sum_{n=1}^\infty a_nである。
ここで逆に， \{a_n\} は \{a_{\varphi(n)}\} の項を ( \varphi^{-1} によって)入れ替えたものと思えるから，逆の不等号も従う。
以上から，
\sum_{n=1}^\infty a_{\varphi(n)} = \sum_{n=1}^\infty a_nであることが分かった。
証明終
一般の実数または複素数の場合
上の正項級数の場合の結果を用いずに証明します。
証明
L = \sum_{n=1}^\infty a_n とし， \varepsilon > 0 とおく。
このとき，ある N_1 \ge 1 が存在して，
n \ge N_1 \implies \left| \sum_{k=1}^n a_k - L \right| < \varepsilonとできる。また絶対収束することから，ある N_2 \ge 1 が存在して，
n \ge N_2 \implies \sum_{k=n}^\infty | a_k | < \varepsilonも成立する。このとき， N = \max\{N_1, N_2 \} と定めよう。
ここで， M \ge 1 を
\{\varphi(k) \mid 1 \le k \le M\} \supset \{k \mid 1 \le k \le N\}
となるように，十分大きくとることにする。（すなわち， M \ge \max_{1\le k \le N} \varphi^{-1} (k) とする。）このとき， n \ge M に対して，
\begin{aligned} &\left| \sum_{k=1}^n a_{\varphi(k)} - L \right| \\ &= \left| \sum_{k=1}^N a_k + \sum_{\substack{1\le k \le n, \\\varphi(k) \ge N+1}} a_{\varphi(k)} - L \right| \\ &\le \left| \sum_{k=1}^N a_k - L \right| + \left| \sum_{\substack{1\le k \le n, \\\varphi(k) \ge N+1}} a_{\varphi(k)} \right| \\ &\le \varepsilon + \sum_{k=N+1}^\infty |a_k| \\ &\le 2\varepsilon \end{aligned}となる。よって結局，
\sum_{n=1}^\infty a_{\varphi(n)} = Lとなり，証明が終わる。
証明終
条件収束級数は全く逆のことが成立する
条件収束の場合は，絶対収束の場合とは全く異なり，以下のような定理が成立します。
定理
実数列 \{a_n\} が条件収束する，すなわち \sum_{n=1}^\infty a_n は収束するが， \sum_{n=1}^\infty |a_n| = \infty となるとする。
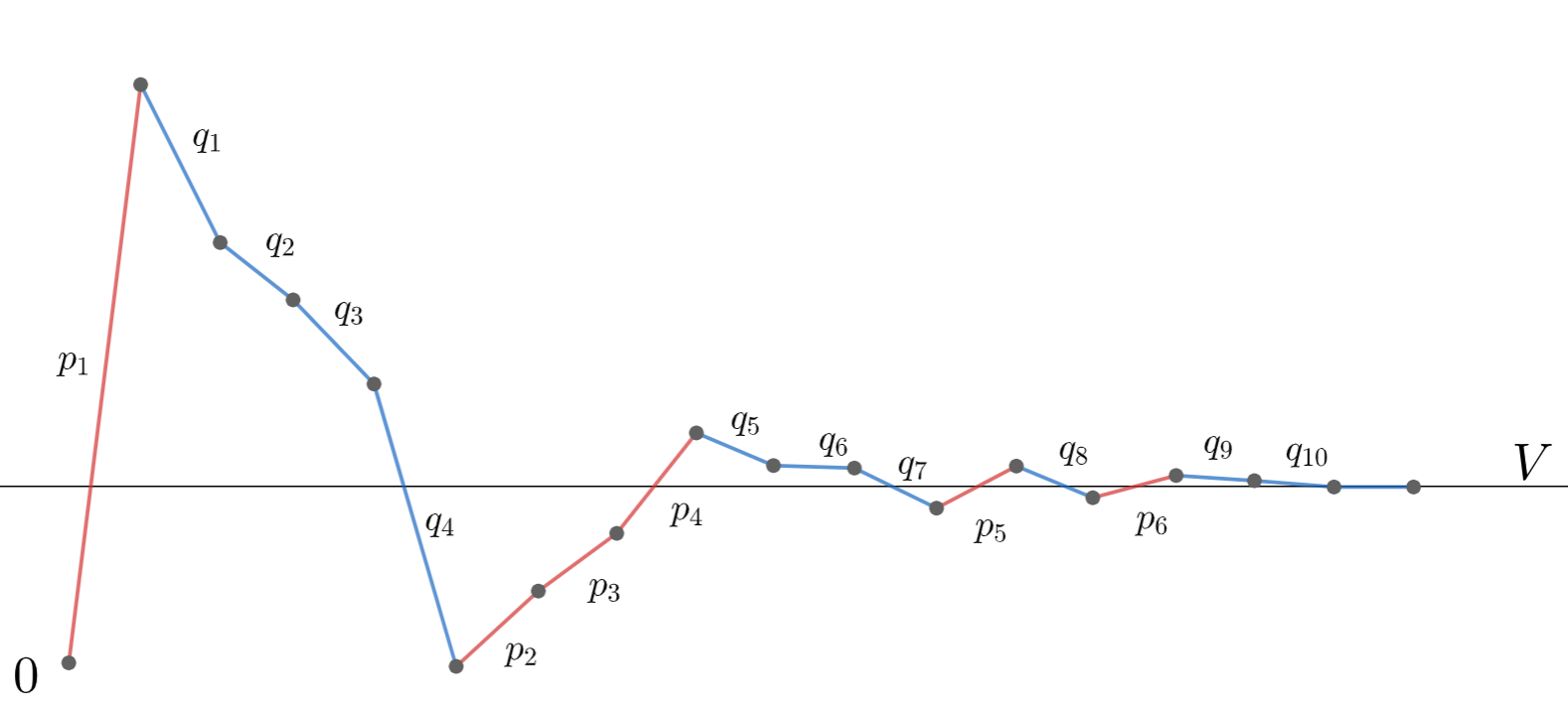
このとき，この数列の和は順序を交換することで，任意の実数または \pm \infty に収束させることができる。
すなわち，任意の V \in [-\infty, \infty] に対して，ある全単射 \varphi \colon \mathbb{Z}_{\ge 1} \to \mathbb{Z}_{\ge 1} が存在して，
とできる。
単に「和の順序によって値が変わる」というよりもはるかに強く，「和の順序の入れ替えによってどんな値にも収束させることができる」と言っているんですね。これの証明は以下の記事で行っていますので，参照してみてください！
