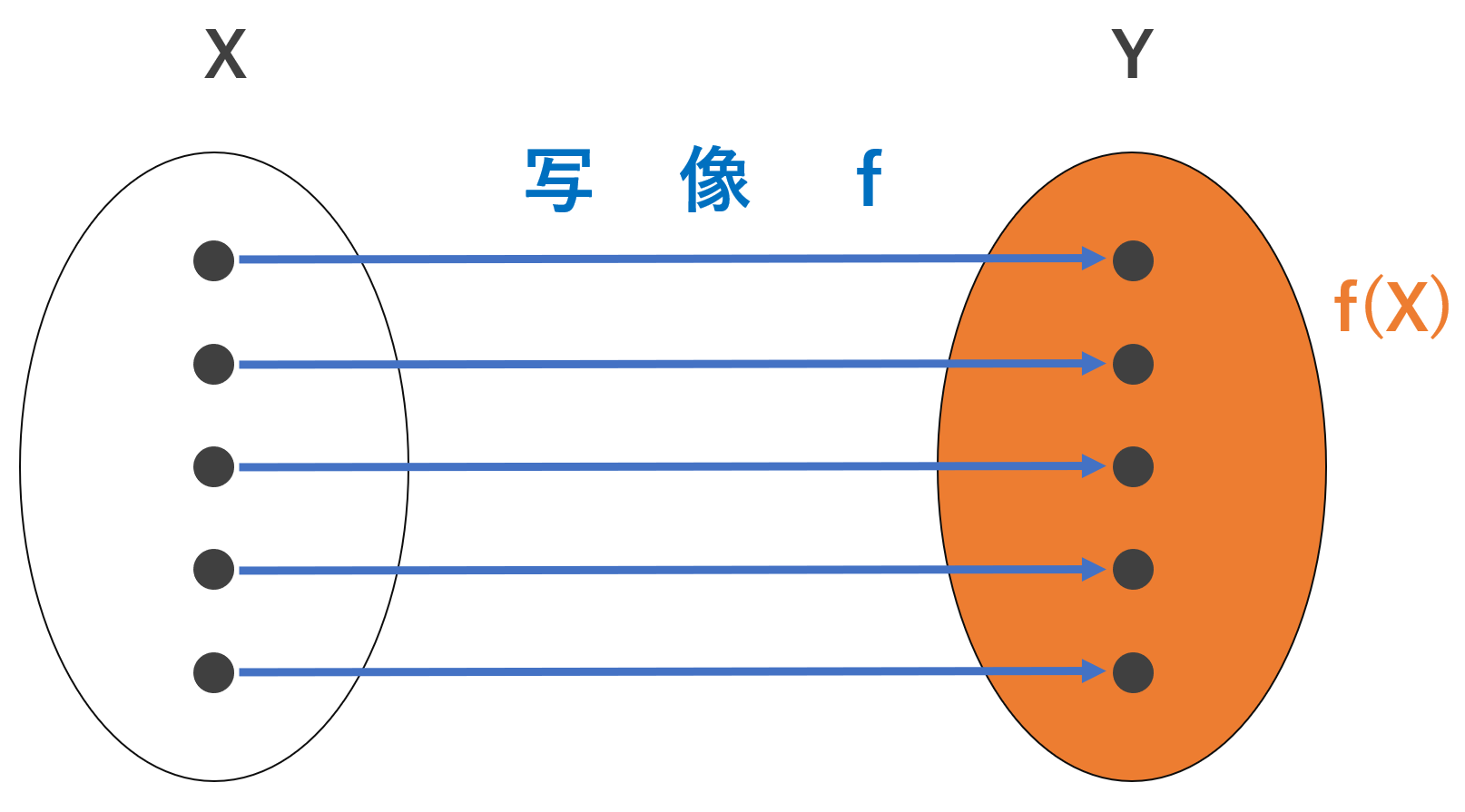
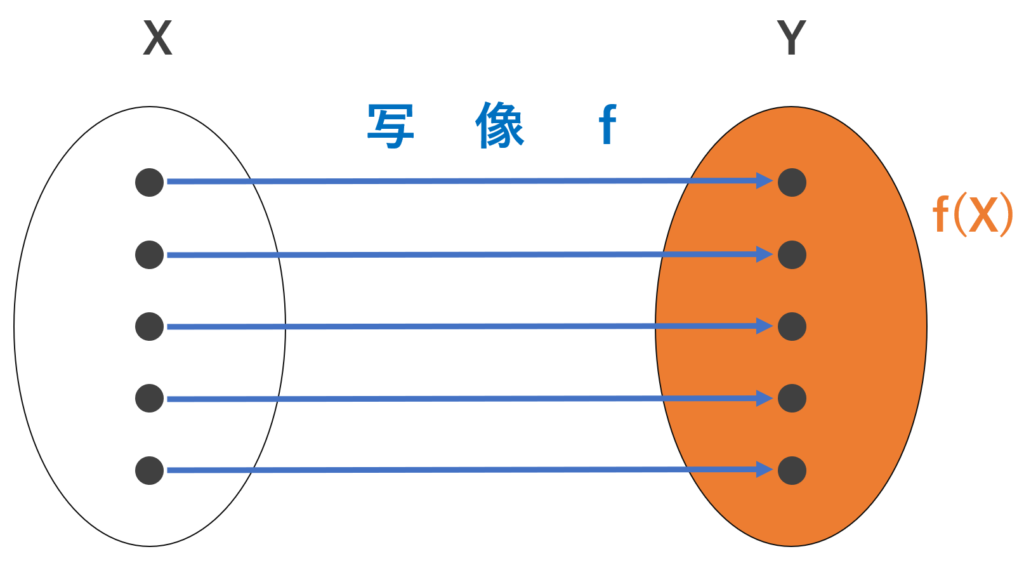
写像・関数を定義する記事で，以下のような図を用いました。
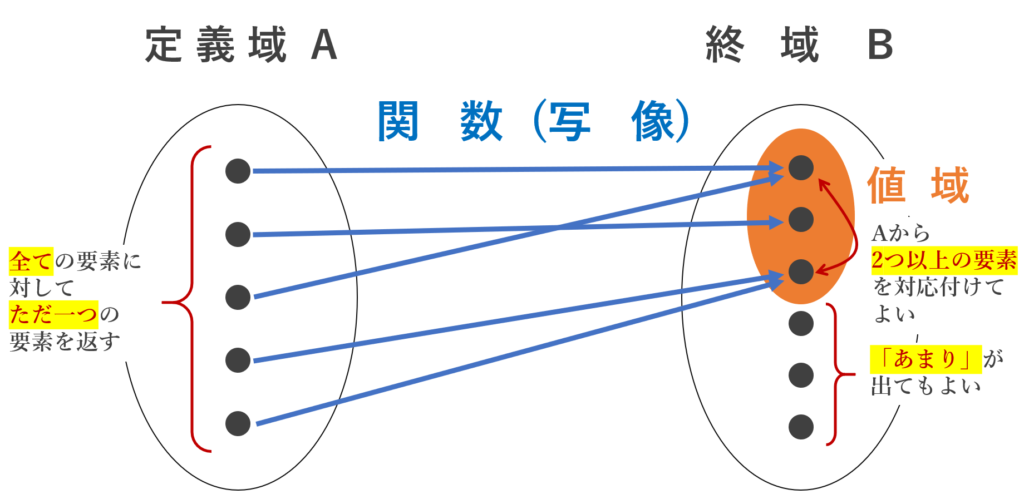
この図において，「あまり」がでない，すなわち，終域と値域が一致するとき，この写像を全射といい，「2つ以上の要素が対応」付かないとき，単射といい，全射かつ単射のとき，全単射といいます。
これについて，もう少し正式に定義し，イメージをもてるようにしましょう。
関数(写像)の定義は既知とします。これについては以下の記事を参照してください。
全射・単射・全単射の定義とイメージ
全射の定義
定義（全射）
f\colon X \to Y が全射または上への写像 (surjective) であるとは，
f(X) = Yとなること（ここで， f(X) = \{f(x) \in Y \mid x \in X \} である）。
すなわち，任意の y \in Y に対して，ある x\in X が存在して， f(x) = y となることである。
このとき，まれに
とかかれる。
終域の方に「あまり」がないということです。
図でイメージすると以下のようになります。
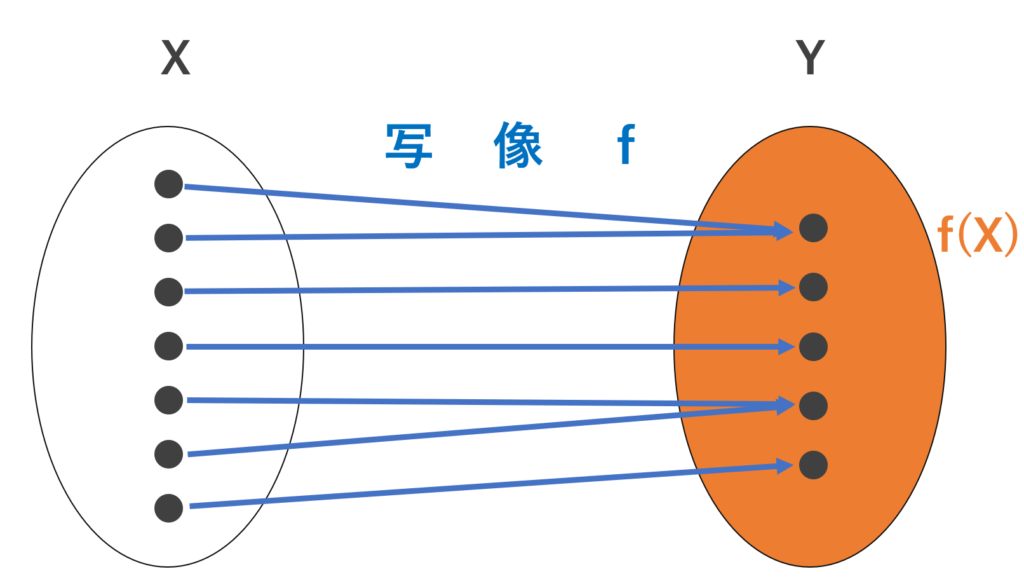
このように， Y の全ての要素に矢印が向いていることが分かると思います。
単射の定義
定義（単射）
f\colon X \to Y が単射または1対1写像 (injective) であるとは，
x_1 \ne x_2 \in X \Longrightarrow f(x_1) \ne f(x_2)となること。対偶をとっていいかえると，
f(x_1) = f(x_2) \Longrightarrow x_1 = x_2となることである。
このとき，しばしば
とかかれる。
異なる「矢印」が同じ Y の要素を指さないということです。
図でイメージすると以下のようになります。
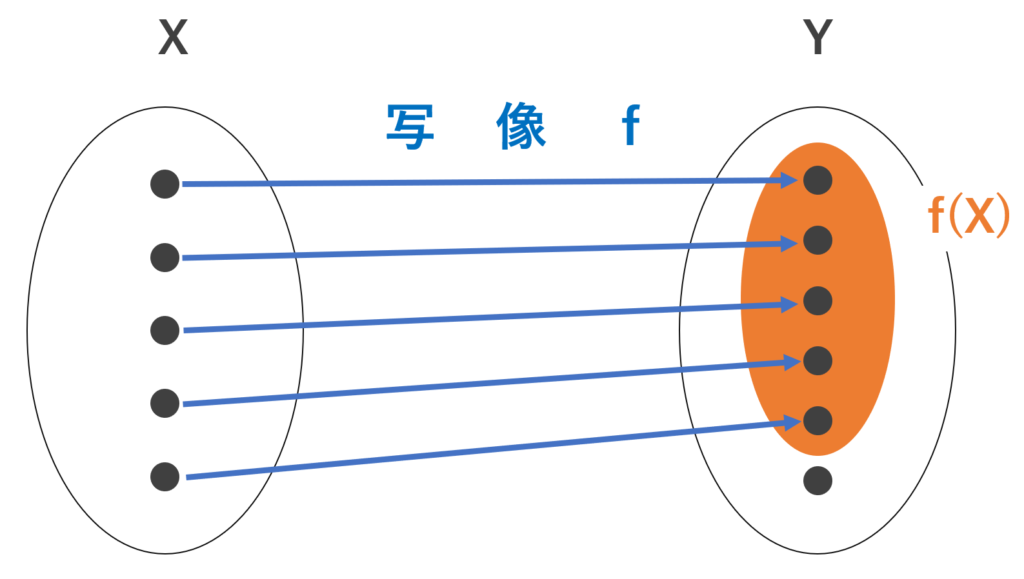
異なる矢印が，別の要素を指していることに注意してください。
全単射の定義
定義（全単射）
f\colon X \to Y が全単射または上への1対1写像 (bijective) であるとは，これが全射かつ単射であること。
すなわち，任意の y \in Y に対して， x \in X がただ一つ存在して， f(x) = y となることである。
全射かつ単射であるため， Y に「あまり」がなく，かつ異なる「矢印」が同じ要素を指さないということです。
図でイメージすると以下のようになります。
「すべて」の要素が「1対1に」対応している様子が分かると思います。
具体例を挙げてみましょう。
全射・単射・全単射の具体例
同じ関数でも，定義域や終域を変えることで，全射になったり単射になったりします。具体例とともに確認していきましょう。
例1.
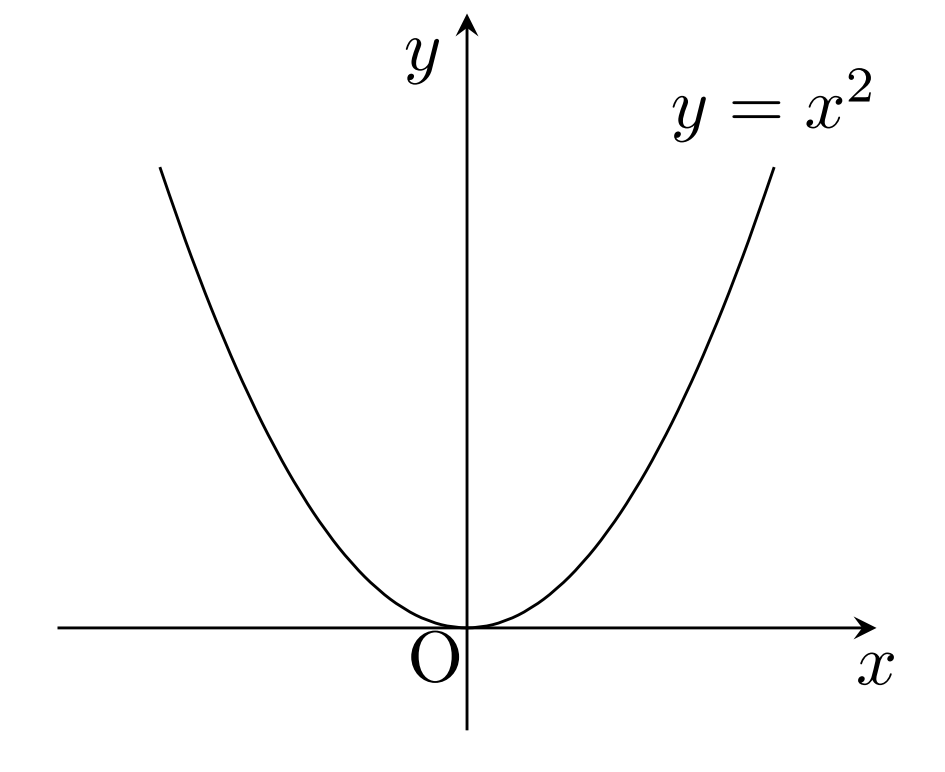
f(x) = x^2 について，
- f\colon \mathbb{R} \to \mathbb{R} で考えると全射でも単射でもない。
- f\colon \mathbb{R} \to [0, \infty) で考えると全射となるが単射ではない。
- f\colon [0, \infty) \to \mathbb{R} で考えると単射となるが全射ではない。
- f\colon [0, \infty) \to [0, \infty) で考えると全単射である。
例2.
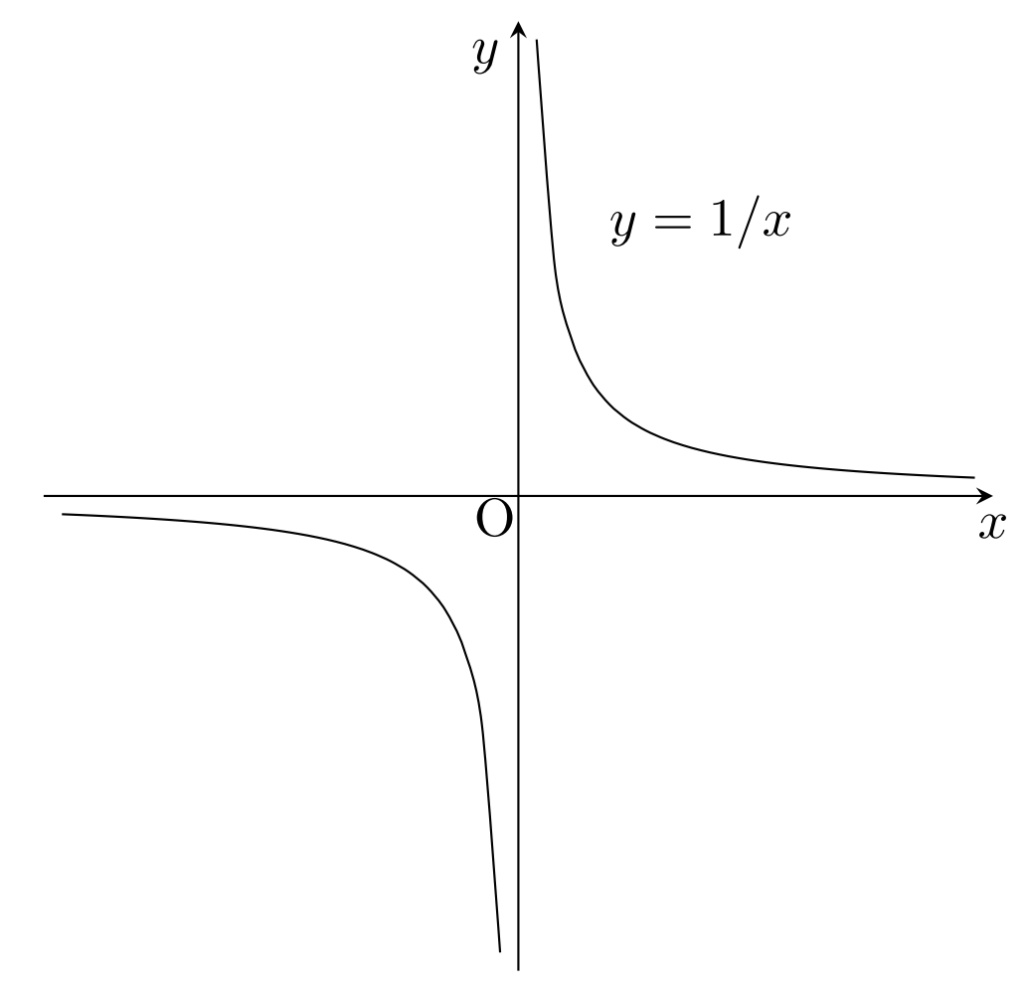
f(x) = 1/x について，
- f\colon \mathbb{R} \setminus\{0\}\to \mathbb{R} \setminus\{0\} で考えて全単射である。
まとめ
いま一度次の4つのイメージ図を見比べてみましょう。
全射でも単射でもない図
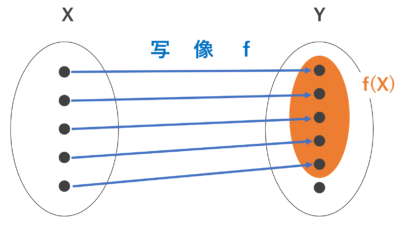
全射だが単射でない図
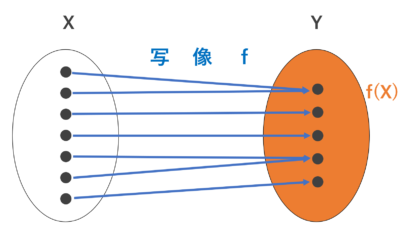
…… Y の全ての要素に矢印が向いている
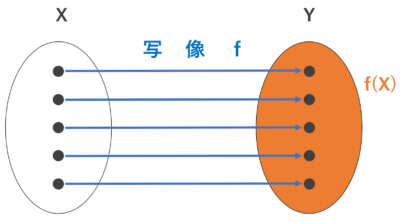
単射だが全射でない図
…… 異なる矢印が，別の要素を指している
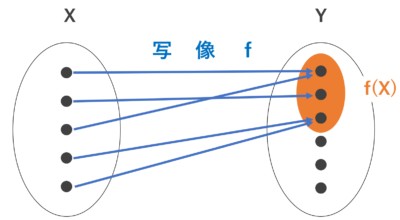
全単射である図
…… 「すべて」の要素が「1対1に」対応している
おわりに
これらのイメージをしっかり持ち，使いこなせるようにしていきましょう。
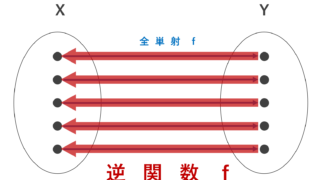
なお，全単射であるとき，逆関数(逆写像)が定義できます。これについては，以下の記事を参照してください。
