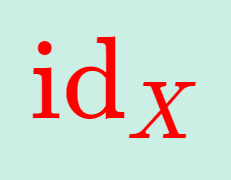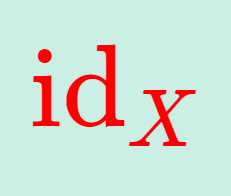逆関数(逆写像)の定義と性質を厳密に～図解付き～

逆関数(逆写像)の定義と性質について図を交えつつ厳密に説明します。

逆関数を厳密に定義するためには，「全単射」という概念が必要です。これについては長くなってしまうため，別の記事で解説しています。以下を参照してください。

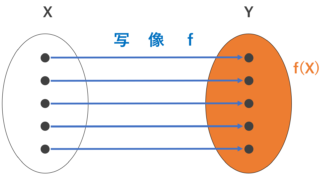
なお，そもそも関数とは何か，写像とは何かについては，以下の記事を参照してください。

ここでは，これらの知識をある程度は知っているものとします。

逆関数(逆写像)の定義

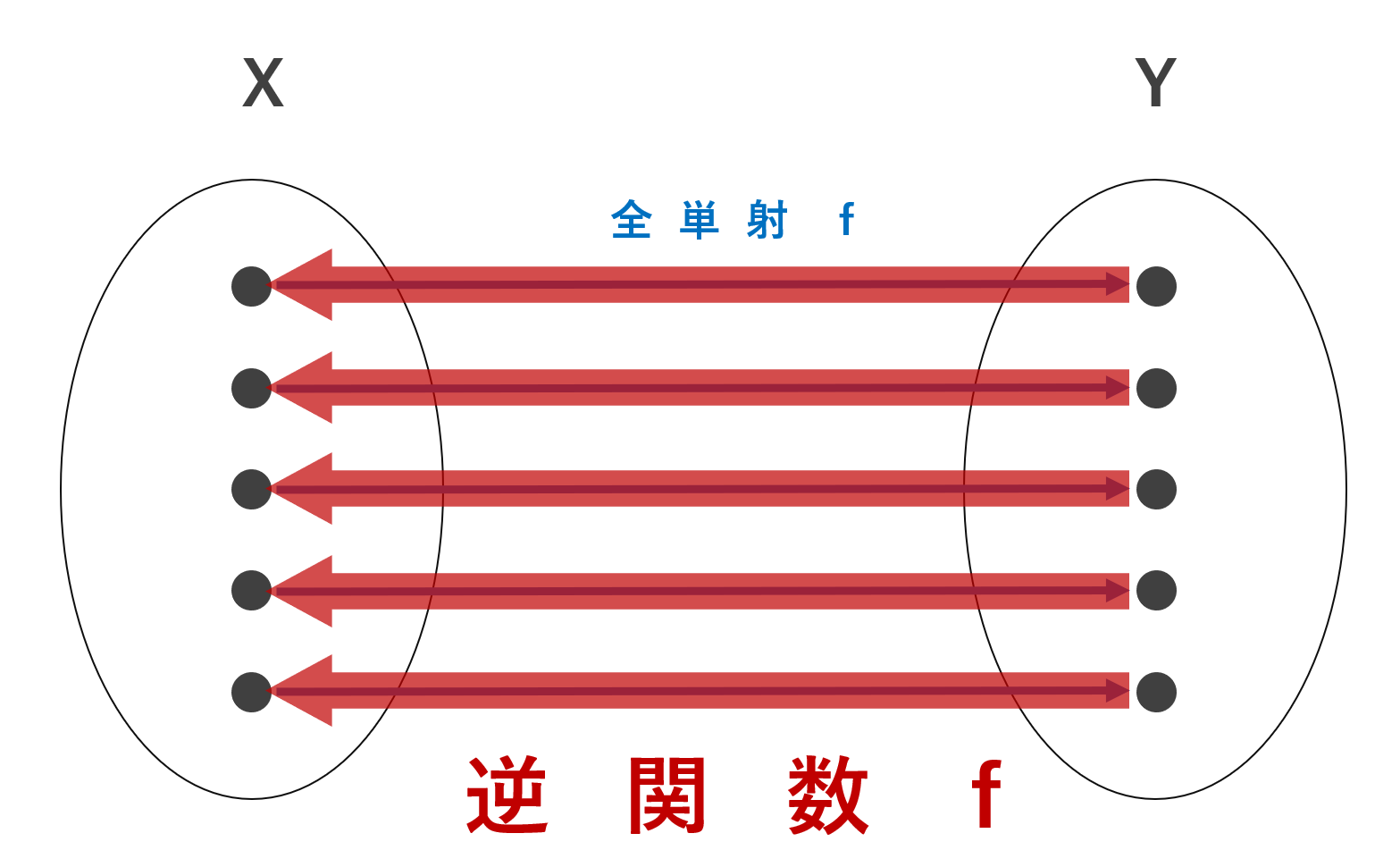
全単射のときはもとの「イメージ図」の矢印を逆転させることで，逆関数(逆写像)を考えることができます。

定義（逆関数・逆写像）

$f\colon X\to Y$ が全単射であるとは，
任意の $y \in Y$ に対して， $x \in X$ がただ一つ存在して， $f(x) = y$ となることであった。

これは， $Y$ から $X$ への関数(写像)とみることができる。これを逆関数 (inverse function)，逆写像 (inverse mapping) といい，

\textcolor{red}{f^{-1} \colon Y \to X }

とかく。このとき，

f(x) = y \Longleftrightarrow f^{-1}(y) = x

である。

図で考えてみましょう。まず以下が「全単射」のイメージ図です。

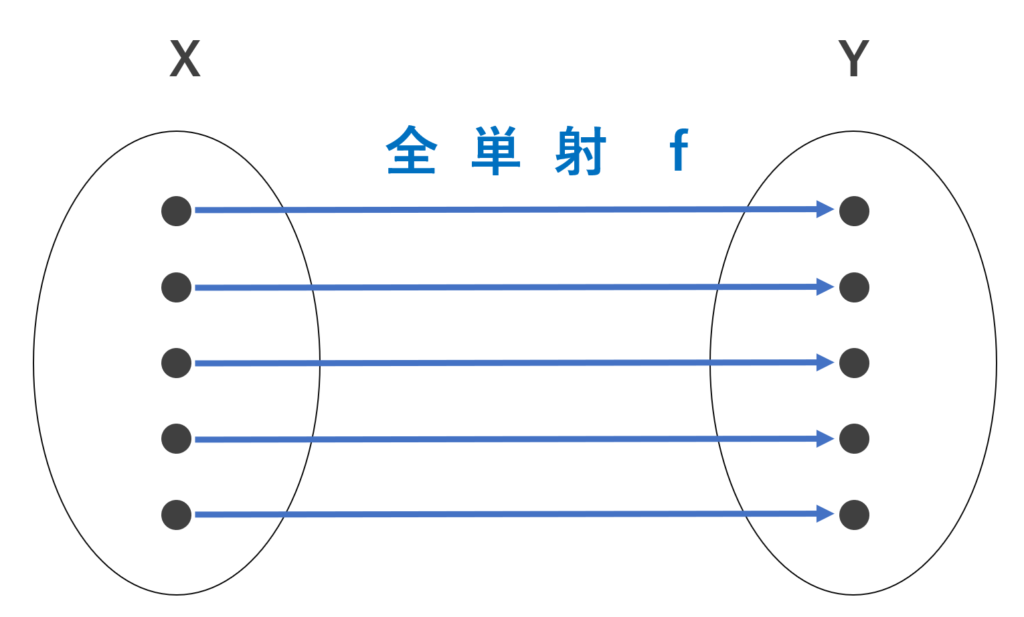
この矢印を全て逆転させることで，逆関数(逆写像)が作れます。

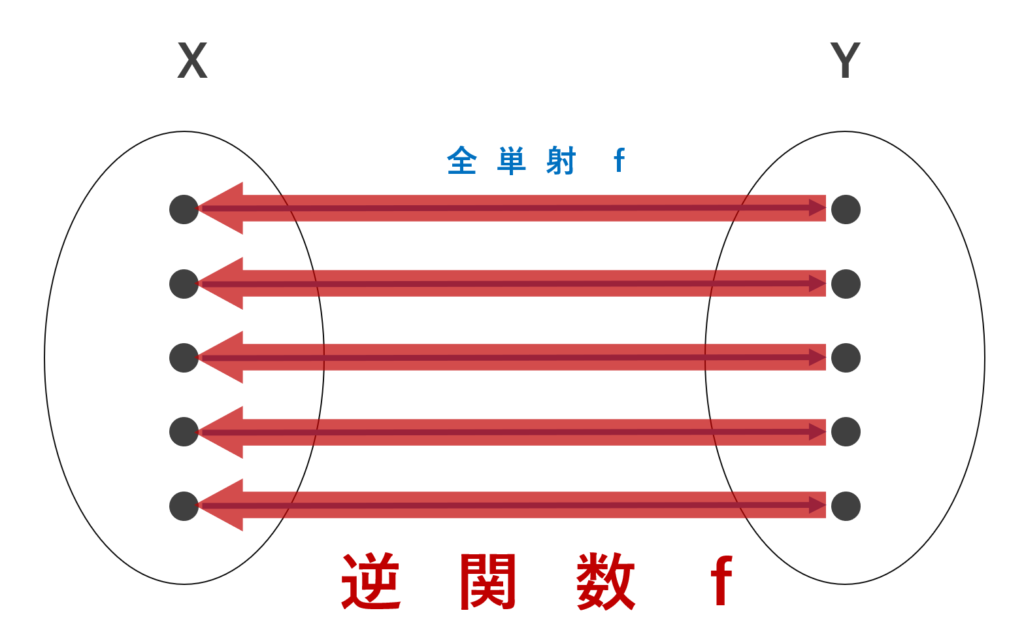
これが，逆関数(逆写像)のイメージです。

ほぼ明らかですが，以下の性質が成立します。

命題（逆関数・逆写像の性質）

$f\colon X \to Y$ を全単射とする。このとき，以下が成立する。

$f^{-1}$ は全単射である。
$(f^{-1})^{-1} = f.$
$X=Y$ とすると， $f \circ f^{-1} = f^{-1} \circ f = \textrm{id}_X.$
$X, Y \subset \mathbb{R}$ とすると， $y=f(x)$ のグラフと $y = f^{-1}(x)$ のグラフは直線 $y = x$ に関して対称である。

ここで， $\textrm{id}_X$ は，定義域と終域がともに $X$ であり， $\textrm{id}_X (x) = x$ となる恒等写像を表します。

恒等写像の定義は以下の記事を参照してください。

最後は，図で考えればほぼ明らかですが，きちんと証明してみましょう。

4.の証明

$y = f(x)$ のグラフは，集合でかくと

\{(a, f(a))\in \mathbb{R}^2 \mid a \in X\}

であることに注意する。これと， $y= x$ に関して対称なグラフは，各点 $(p, q )\in \mathbb{R}^2$ が点 $(q, p)\in \mathbb{R}^2$ にうつるため，

\{(f(a), a)\in \mathbb{R}^2 \mid a \in X\}

とかける。

これは逆関数の定義より， $b = f(a) \,(\Leftrightarrow a = f^{-1} (b) )$ と文字の置換をすることで，

\{(b, f^{-1}(b))\in \mathbb{R}^2 \mid b \in Y\}

と書き直せる。これは $y = f^{-1}(x)$ のグラフそのものである。

証明終

高校数学では，「全単射」の概念を習わないことが多いため，どうしても逆関数の定義は「 $x$ と $y$ を入れ替える」などと曖昧になってしまいがちです。逆関数は全単射であってはじめて定義できる概念であることに注意しましょう。