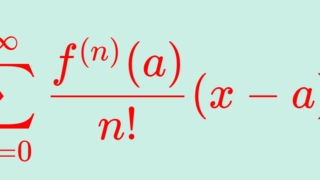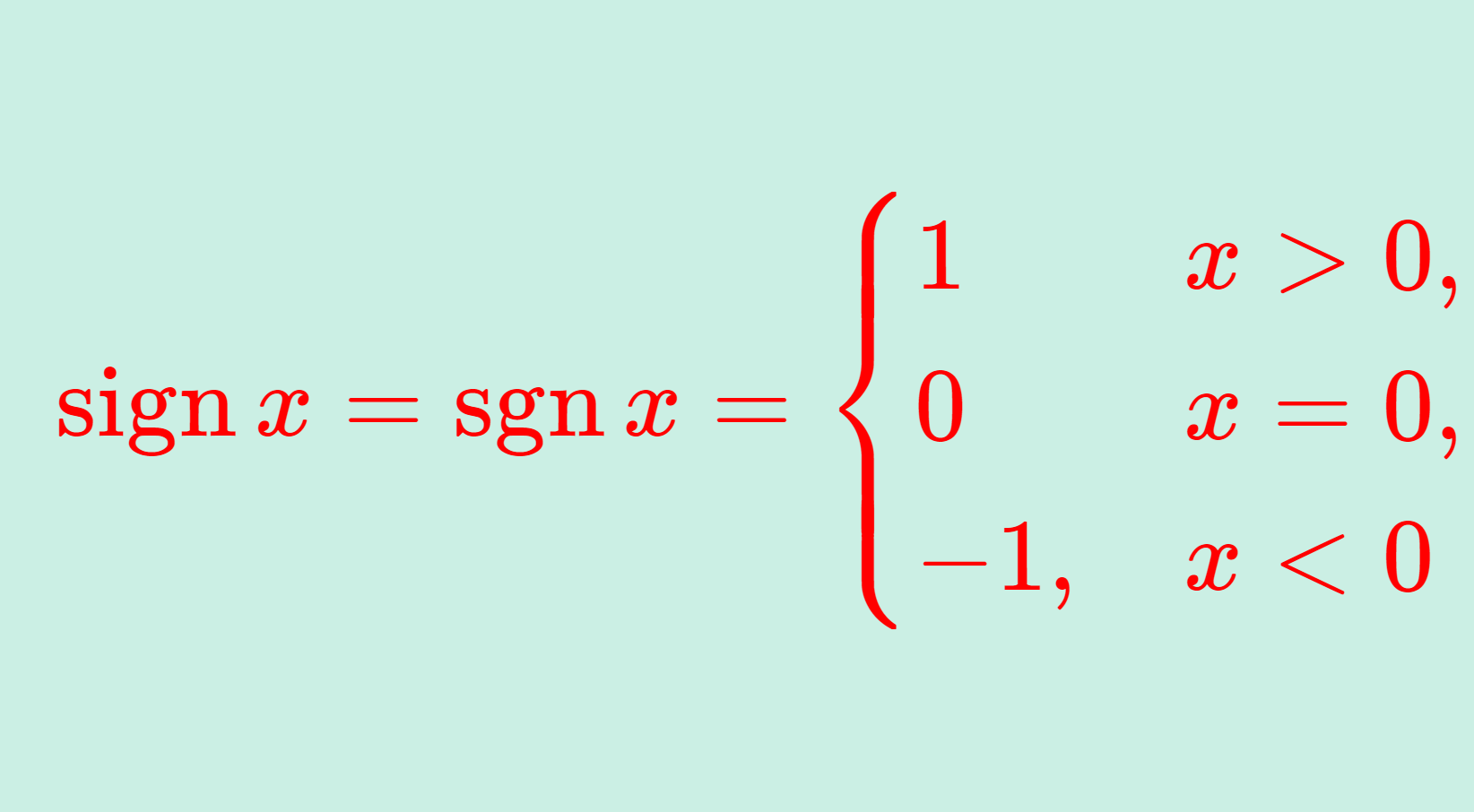C^1 級関数や C^n 級関数, C^\infty 級関数の定義とその具体例について紹介します。
C1級,Cn級,C∞級関数の定義(一変数版)
まずは C^1, C^n , C^\infty 級関数の定義を紹介しましょう。
C1級関数の定義
定義(C^1 級)
f\colon \mathbb{R} \to \mathbb{R} が C^1 級 (class C^1 ) または連続微分可能 (continuously differentiable) であるとは,
- f が微分可能
- 導関数 f^{\prime} が連続
の両方が成立することをいう。
また,このような関数全体の集合を C^1(\mathbb{R}) と書くことがある。
微分可能 \Longrightarrow 連続 なので, f, f^{\prime} の両方が連続になります。
Cn級関数の定義
定義(C^n 級)
f\colon \mathbb{R} \to \mathbb{R} が C^n 級 (class C^n ) または n 階連続微分可能 (n times continuously differentiable) であるとは,
- f が微分可能
- n 階導関数 f^{(n)} が連続
の両方が成立することをいう。
また,このような関数全体の集合を C^n(\mathbb{R}) と書くことがある。
微分可能 \Longrightarrow 連続 なので, f, f^{\prime},\ldots,f^{(n)} の全てが連続になります。
C∞級関数の定義
定義(C^\infty 級)
f\colon \mathbb{R} \to \mathbb{R} が C^\infty 級 (class C^\infty ) または 無限回微分可能 (infinitely differentiable) であるとは,
- f が何回でも微分できる
ことをいう。
また,このような関数全体の集合を C^\infty(\mathbb{R}) と書くことがある。
微分可能 \Longrightarrow 連続 なので, f, f^{\prime},\ldots,f^{(n)},\ldots の全てが連続になります。
このとき,以下が成立します。
命題
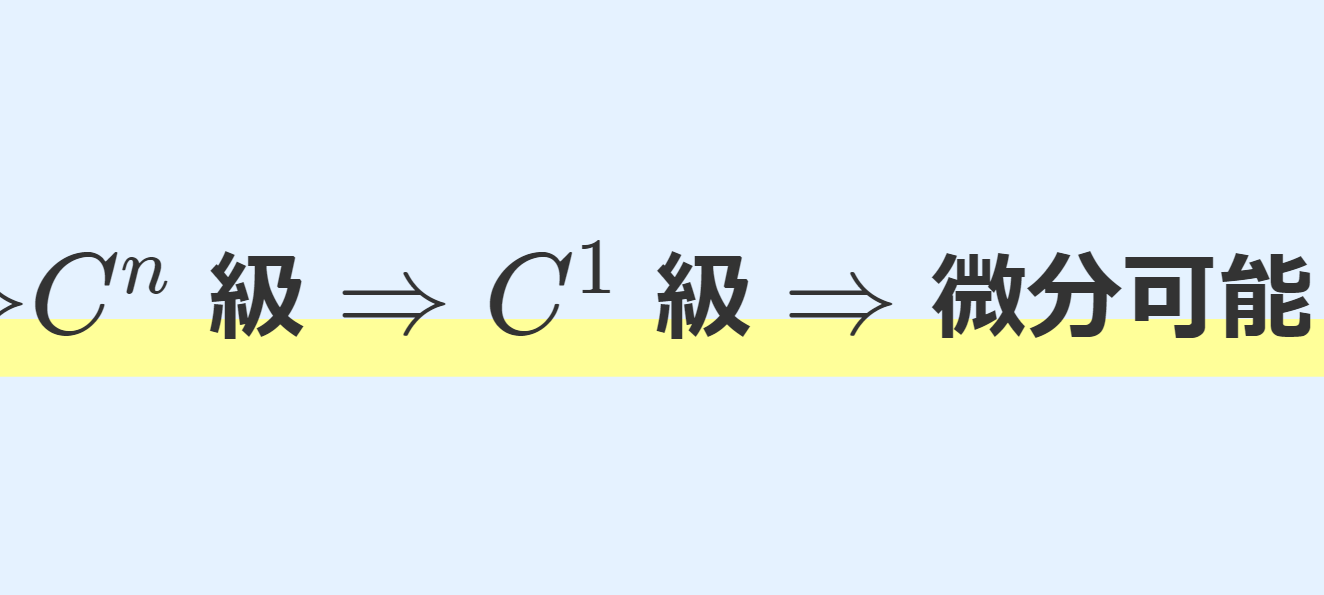
C^\infty 級 \Rightarrow C^n 級 \Rightarrow C^1 級 \Rightarrow 微分可能 \Rightarrow 連続
であり,すべてにおいて逆は成り立たない。集合を用いてかくと,
C^\infty(\mathbb{R}) \subsetneq C^n(\mathbb{R}) \subsetneq C^1(\mathbb{R}) \subsetneq 微分可能関数全体の集合 \subsetneq C(\mathbb{R})
である。ただし, C(\mathbb{R}) は連続関数全体の集合を指す。
ちなみに,単に連続な関数のことを, C^0 級関数ということがあります。
また,C^\infty 級よりもさらに強い概念として,解析的 (analytic) というのもあります。同じ意味で, C^\omega 級ということもあります。これは,テイラー展開・マクローリン展開とよばれる「べき級数展開」に関係するものです。これについては,以下の記事を参照してください。
C1級,Cn級,C∞級関数の具体例5個
典型的な具体例を述べましょう。
例1.(連続だが微分可能でない例)
\textcolor{red}{f(x) = |x| }は連続だが微分可能でない。
原点で微分できませんね。
例2.(微分可能だが C^1 級でない例)
\textcolor{red}{f(x) = \begin{cases} x^2 \sin \frac{1}{x} & x \ne 0,\\ 0 & x = 0 \end{cases}}は微分可能だが C^1 級でない。
実際,
f^{\prime} (x) = \begin{cases} 2x \sin \frac{1}{x} - \cos \frac{1}{x} & x \ne 0,\\ 0 & x = 0\end{cases}であるから, f^{\prime} は原点で連続になりません。
例3.( C^1 級だが,C^2 級でない例)
\textcolor{red}{f(x) = x|x| }は C^1 級だが,f^{\prime} は微分可能でない。
実際,
f^{\prime}(x) = |x|になるため,これは原点で微分できません。
例4.( C^{n} 級だが,C^{n+1} 級でない例)
n \ge 1 とする。
\textcolor{red}{f(x) = \begin{cases} x^{n+1} & x \ge 0, \\ - x^{n+1} & x < 0 \end{cases}}とおくと,これは C^{n} 級だが,f^{(n)} は微分可能でない。
実際,
f^{(n)} (x) = (n+1)! \, |x|となるため,これは原点で微分不可能です。
例5.( C^\infty 級関数の例)
\textcolor{red}{ \begin{aligned} f_1(x) &= e^x \\ f_2(x) &= \sin x\\ f_3(x) &= 1 \\ f_4(x) &= \frac{1}{1+x^2} \end{aligned} }などは全て C^\infty 級関数である。
ほぼ明らかでしょう。
多変数の場合のC1級,Cn級,C∞級関数
最後に d 次元空間 \mathbb{R^d} 上での定義を述べましょう。
定義(C^1 級;多変数版)
f\colon \mathbb{R^d} \to \mathbb{R} が C^1 級 (class C^1 ) であるとは,
- f が 1 階のあらゆる偏導関数 f_{x_1}, \ldots ,f_{x_d} をもつ
- それらがすべて連続
の両方が成立することをいう。
また,このような関数全体の集合を C^1(\mathbb{R^d}) と書くことがある。
定義(C^n 級;多変数版)
f\colon \mathbb{R^d} \to \mathbb{R} が C^n 級 (class C^n ) であるとは,
- f が n 階のあらゆる偏導関数をもつ
- それらがすべて連続
の両方が成立することをいう。
また,このような関数全体の集合を C^n(\mathbb{R^d}) と書くことがある。
このとき, n 回までの偏微分は微分の順序によらないことが証明できます(シュワルツの定理)。
定義(C^\infty 級;多変数版)
f\colon \mathbb{R^d} \to \mathbb{R} が C^\infty 級 (class C^\infty ) であるとは,
- f が無限回偏微分可能
であることをいう。
また,このような関数全体の集合を C^\infty(\mathbb{R^d}) と書くことがある。
おわりに
よく出てくる用語ですから,しっかりとおさえておきましょう。