 数論
数論 ピタゴラス数一覧【10000以下全て1593個】
a^2+b^2=c^2をみたす整数の組(a,b,c)をピタゴラス数 (Pythagorean triple) といい,特にa,b,cの3数の最大公約数が1であるものを 原始ピタゴラス数 (primitive Pythagorean triple) といいます。今回は,以下のルールに従い,ピタゴラス数をひたすら列挙します。
 数論
数論 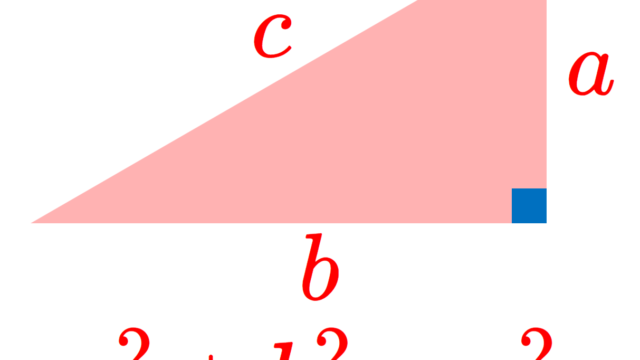 数論
数論  数論
数論  数論
数論  数論
数論 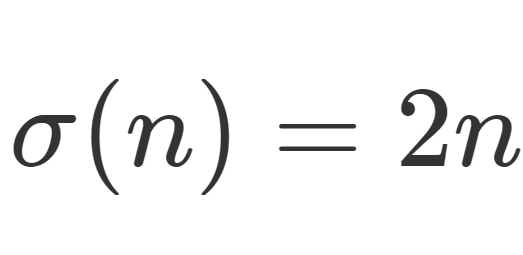 数論
数論 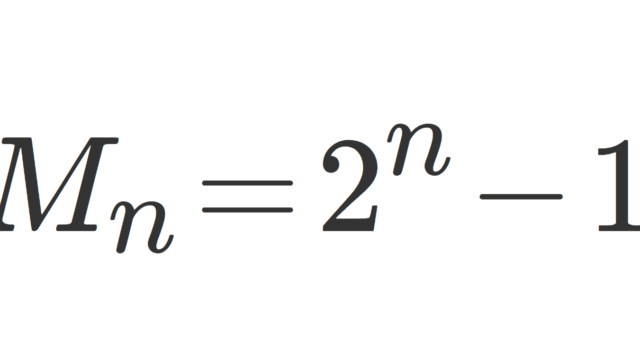 数論
数論 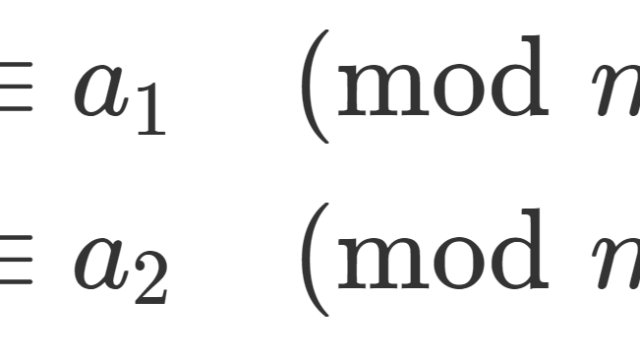 数論
数論 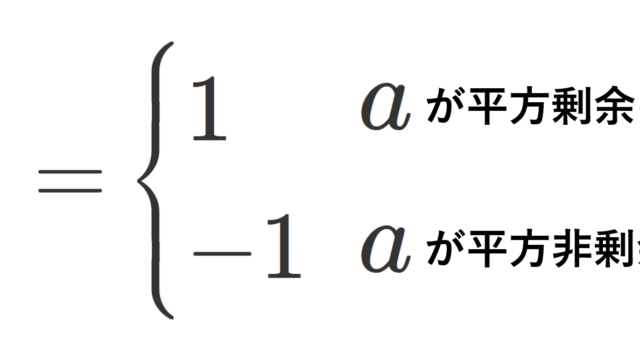 数論
数論 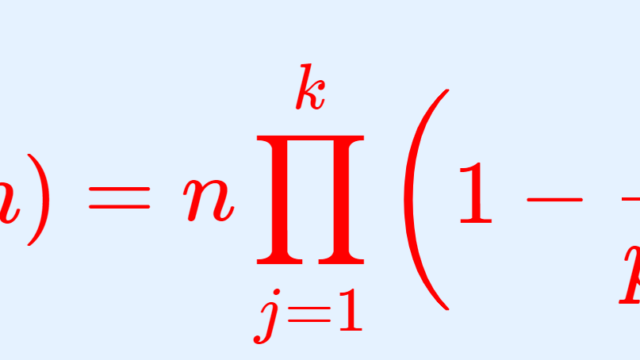 数論
数論