 群・環・体
群・環・体 巡回群とは~定義・例・性質~
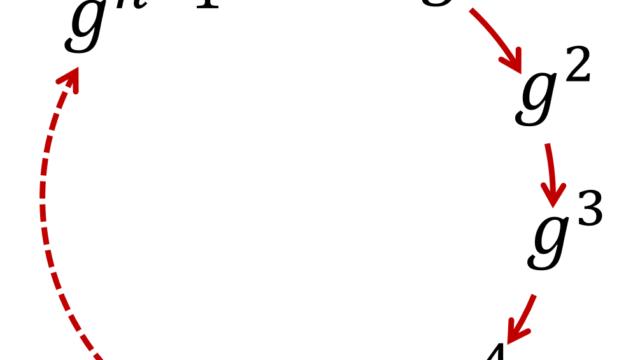
巡回群 (cyclic group) とは,唯一つの元で生成される群を指します。巡回群について,その定義と例・性質4つを順番に紹介しましょう。
 群・環・体
群・環・体  群・環・体
群・環・体  群・環・体
群・環・体  群・環・体
群・環・体  数論
数論 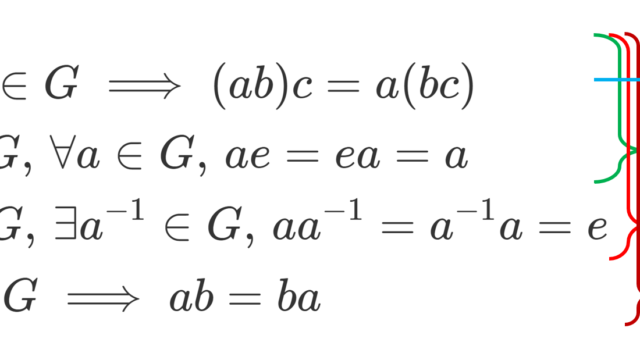 群・環・体
群・環・体 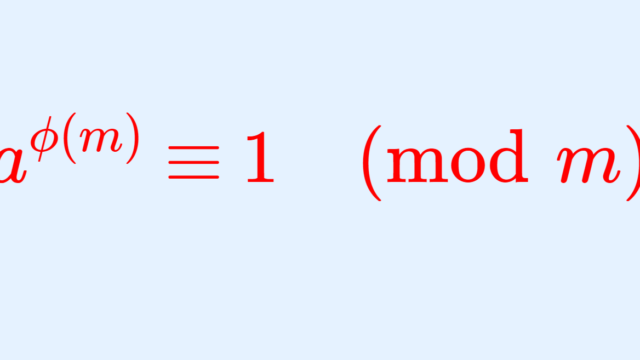 数論
数論 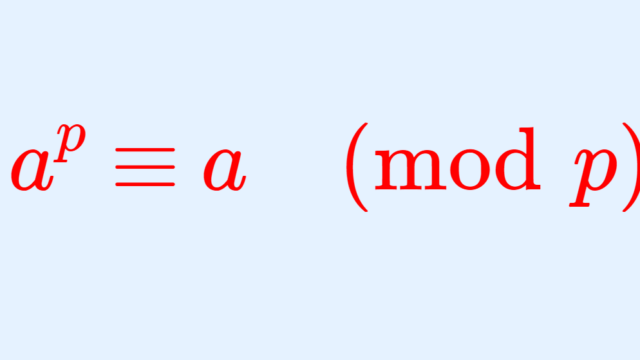 数論
数論  数論
数論  線形代数学
線形代数学