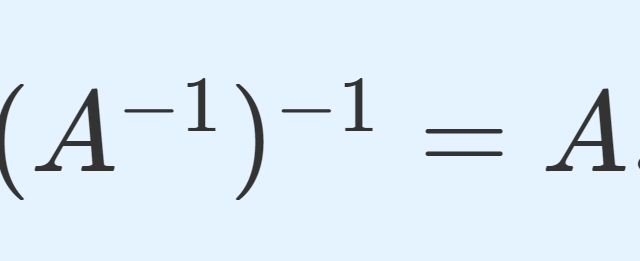 線形代数学
線形代数学 正則行列とは~定義と性質11個とその証明~
正方行列が正則 (regular),あるいは単に正則行列 (regular matrix) であるとは,逆行列が存在することを指します。これについて,その定義と性質11個(逆行列の一意性,正則行列と積・転置・行列式・固有値との関係など)を,証明付きで順に紹介しましょう。
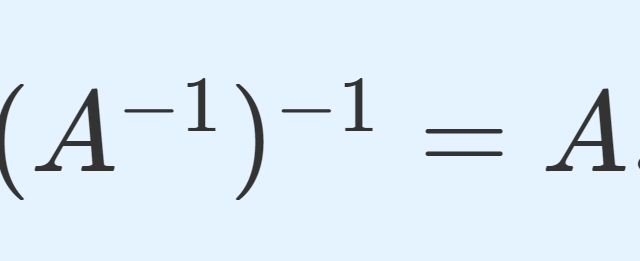 線形代数学
線形代数学  線形代数学
線形代数学 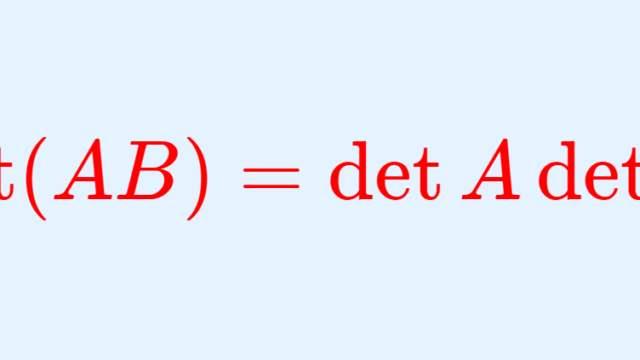 線形代数学
線形代数学 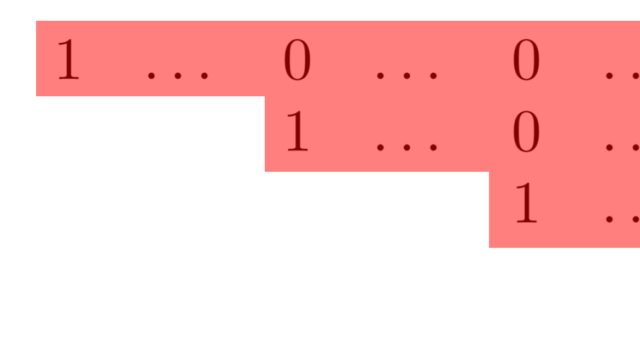 線形代数学
線形代数学 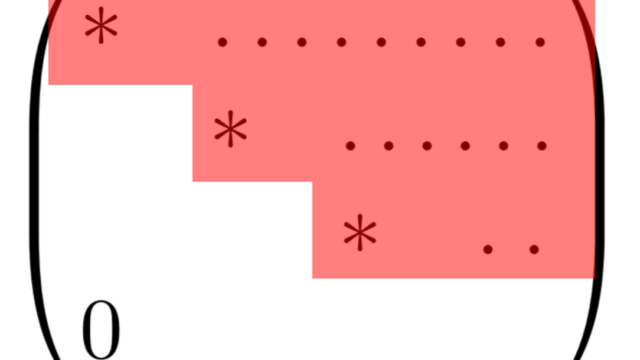 線形代数学
線形代数学 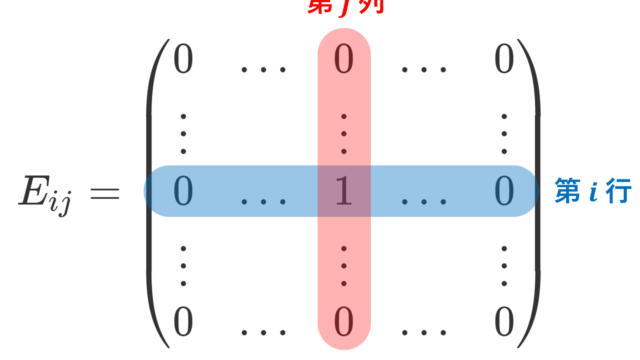 線形代数学
線形代数学 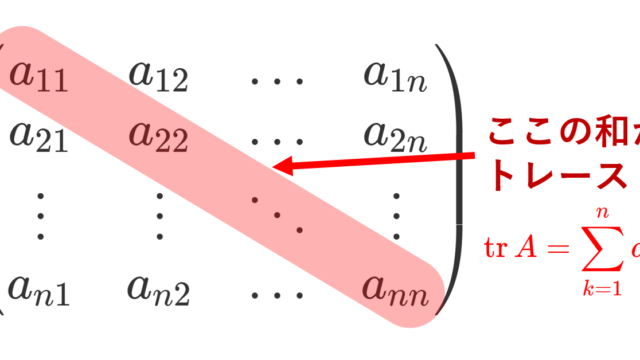 線形代数学
線形代数学  線形代数学
線形代数学  数論
数論 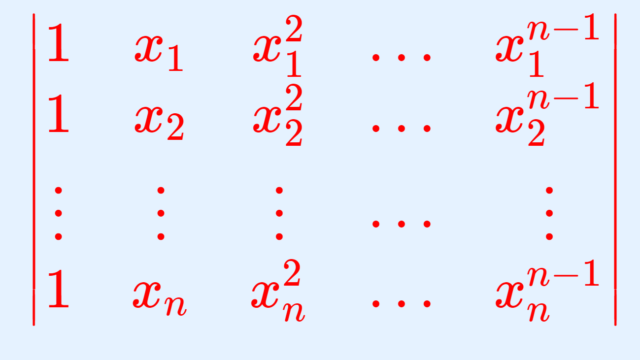 線形代数学
線形代数学