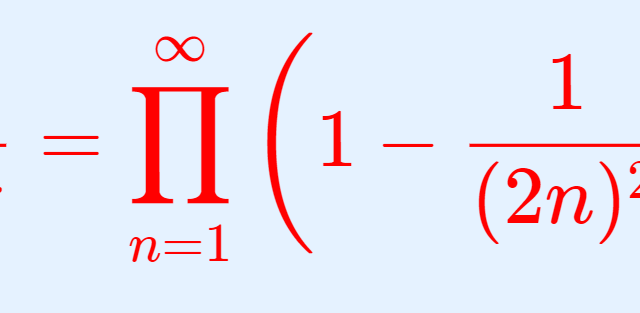 微分積分学(大学)
微分積分学(大学) ウォリスの公式3つとその証明
ウォリスの公式 (Wallis formula,ワリスの公式) と呼ばれる公式を3つの形で紹介し,それらの公式を証明します。円周率πが登場するきれいな公式の1つです。
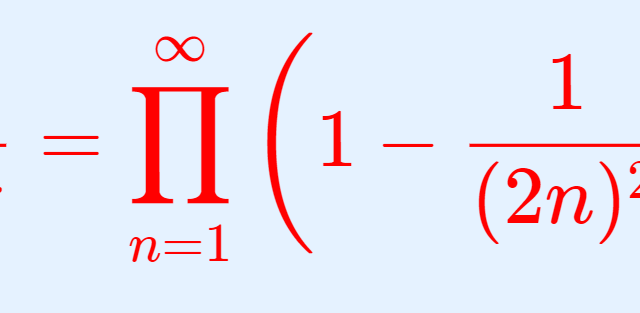 微分積分学(大学)
微分積分学(大学) 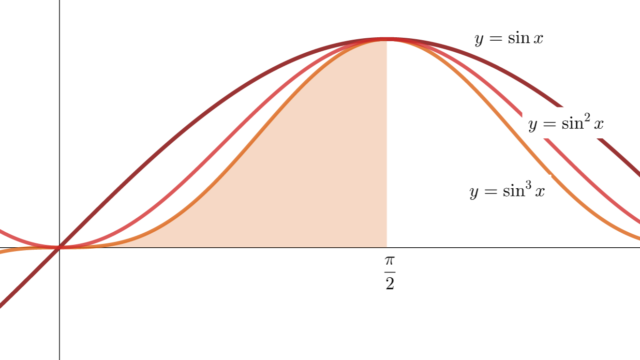 微分積分学(大学)
微分積分学(大学) 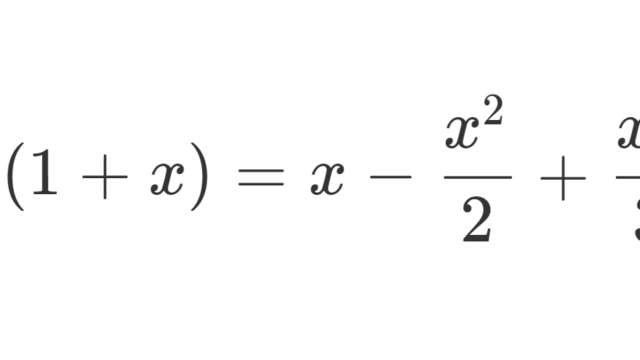 微分積分学(大学)
微分積分学(大学) 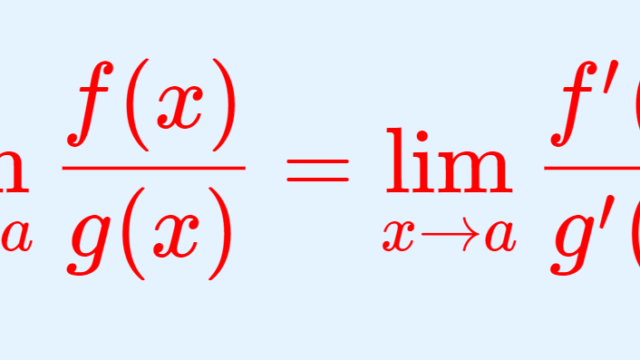 微分積分学(大学)
微分積分学(大学) 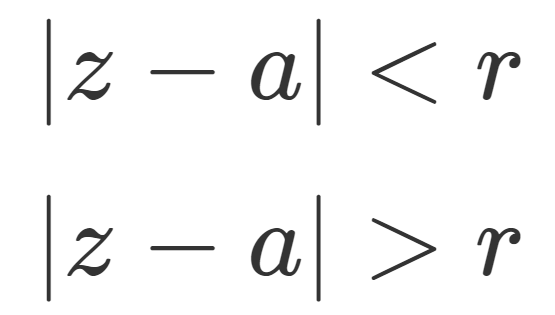 微分積分学(大学)
微分積分学(大学) 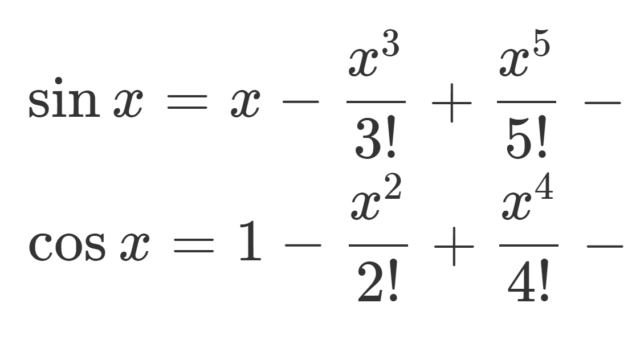 微分積分学(大学)
微分積分学(大学) 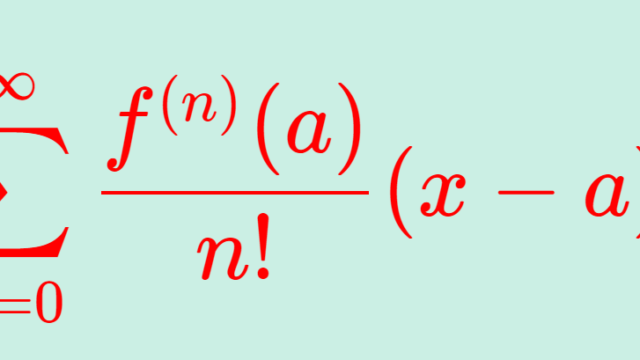 微分積分学(大学)
微分積分学(大学) 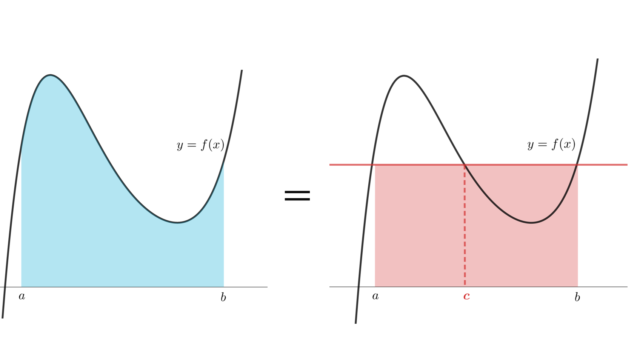 微分積分学(大学)
微分積分学(大学) 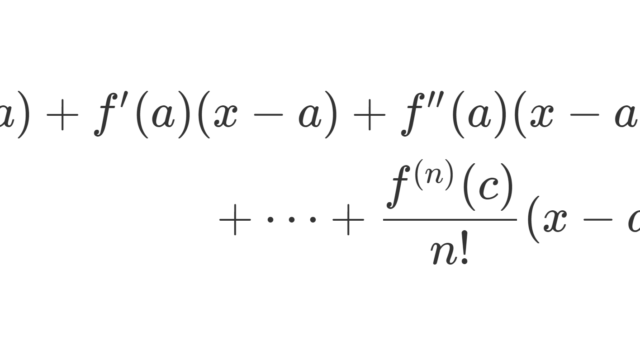 微分積分学(大学)
微分積分学(大学) 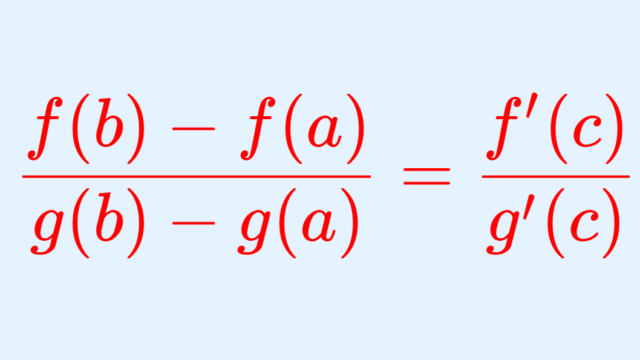 微分積分学(大学)
微分積分学(大学)