 微分積分学(大学)
微分積分学(大学) 方向微分とは~定義・性質・求め方を詳しく~
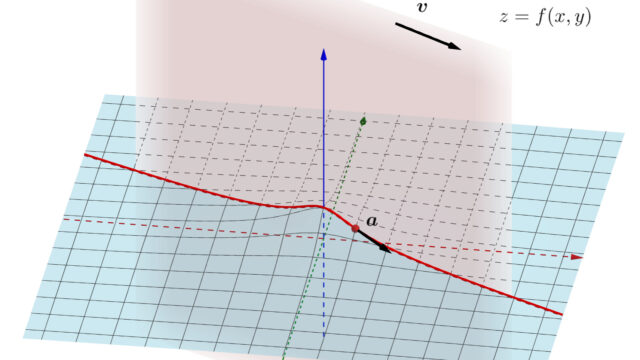
多変数関数における「方向微分」ないしは「方向微分係数」(directional derivative) とは,ある方向のみを取り出した微分を指します。これについて,その定義と性質・求め方を詳しく解説しましょう。
 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  統計学
統計学 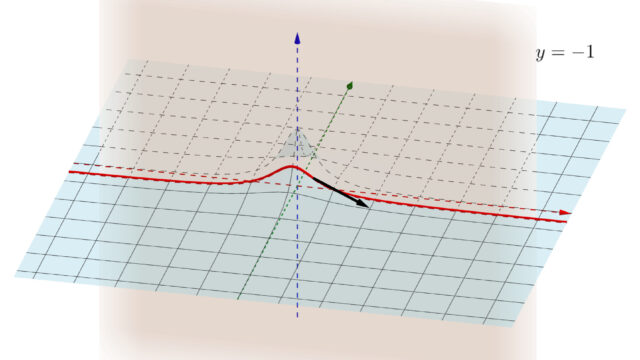 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  確率論
確率論 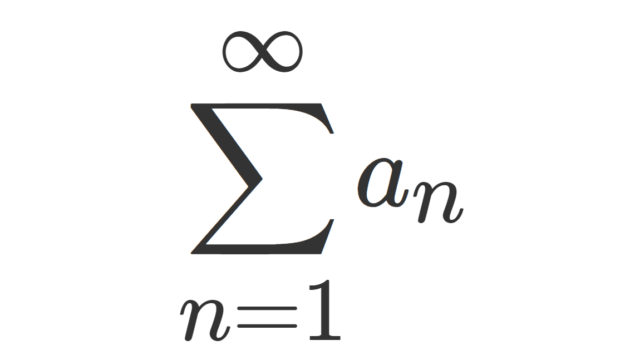 微分積分学(大学)
微分積分学(大学) 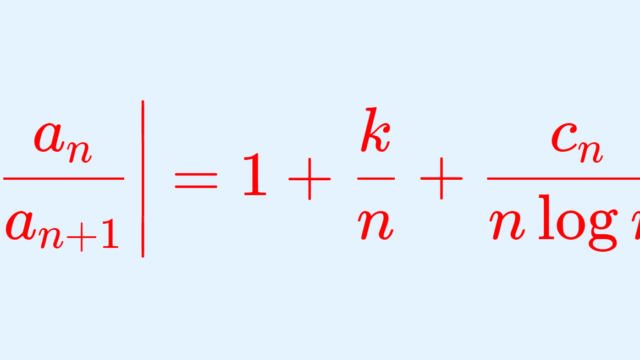 微分積分学(大学)
微分積分学(大学)