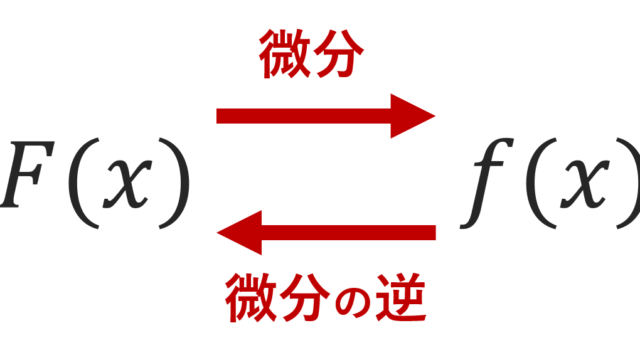
 微分積分学(大学)
微分積分学(大学) 原始関数・不定積分の厳密な定義とその違い
ときに出てくる2つの言葉である「原始関数」と「不定積分」について,その専門数学における厳密な定義と違いについて述べ,理解を深めましょう。おいては,原始関数と不定積分は同じものと定義されます。今回はその立場を取らず,原始関数と不定積分は違うものとして定義します。
 微分積分学(大学)
微分積分学(大学) 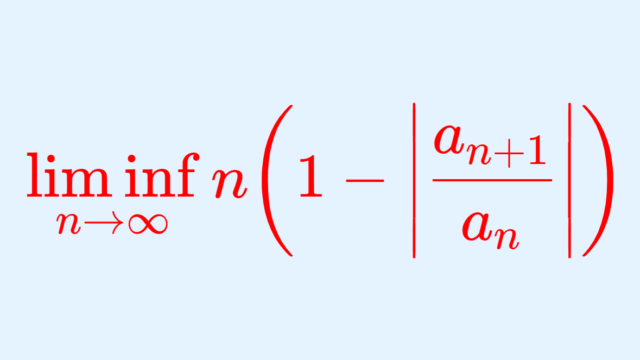 微分積分学(大学)
微分積分学(大学) 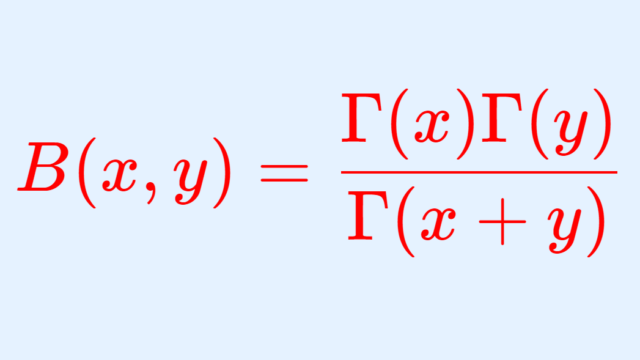 微分積分学(大学)
微分積分学(大学) 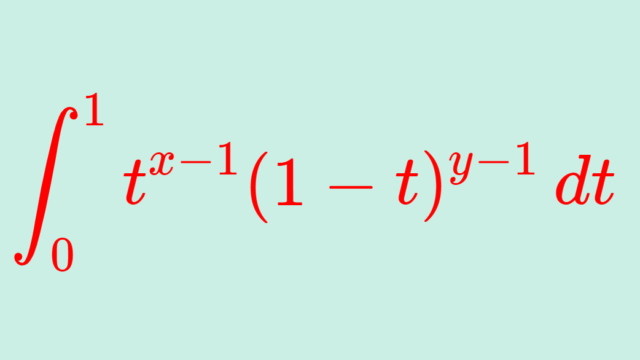 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  確率論
確率論  集合と位相
集合と位相 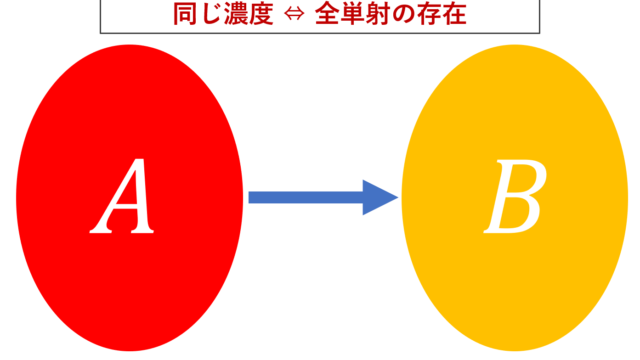 集合と位相
集合と位相 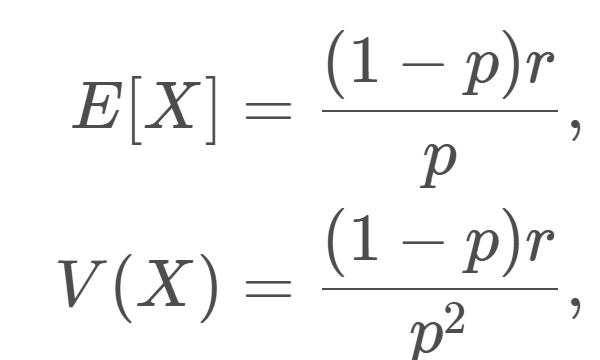 確率論
確率論 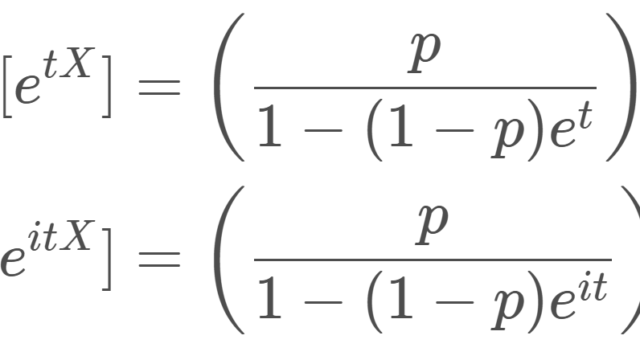 確率論
確率論