 集合と位相
集合と位相 開写像・閉写像の定義・具体例10個・性質4つ
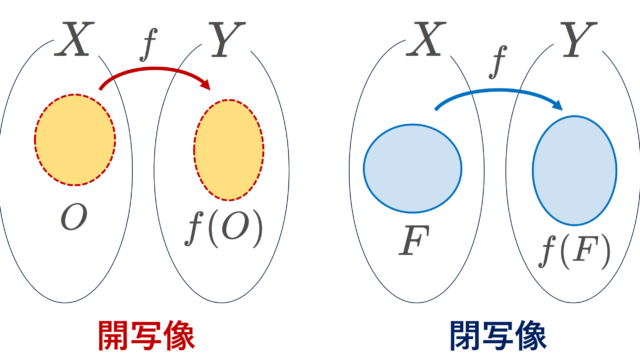
開写像とは,開集合の像(image)を開集合にうつす写像のことで,閉写像とは,閉集合の像(image)を閉集合にうつす写像のことです。開集合・閉写像の定義と具体例・性質を,連続写像と絡めながら,解説しましょう。
 集合と位相
集合と位相 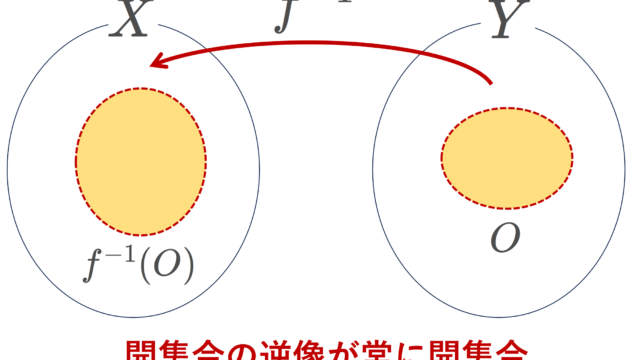 集合と位相
集合と位相 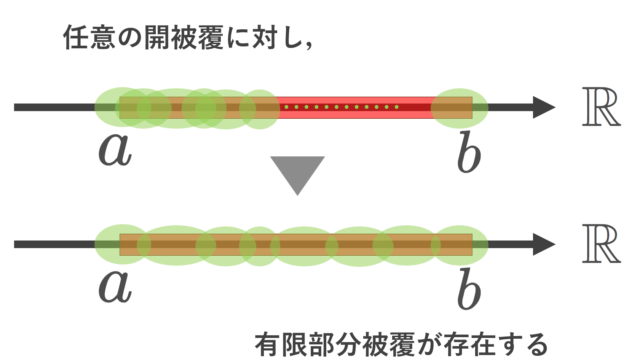 集合と位相
集合と位相 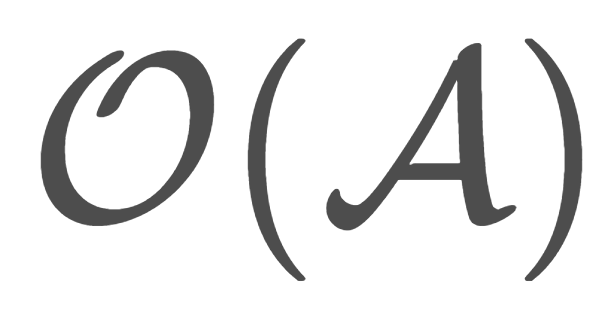 集合と位相
集合と位相 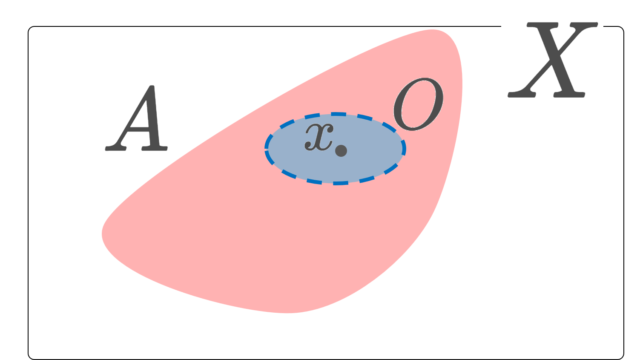 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 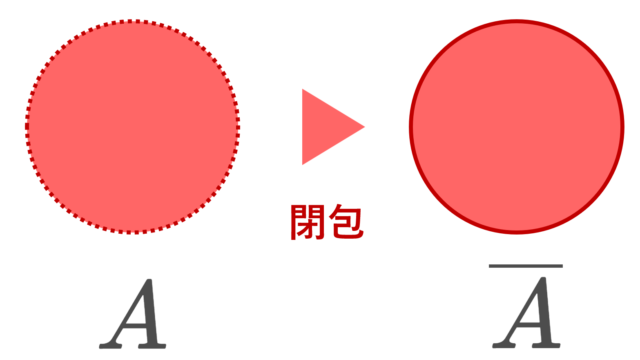 集合と位相
集合と位相 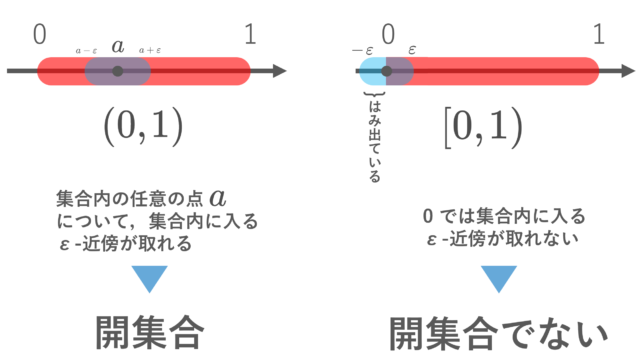 集合と位相
集合と位相 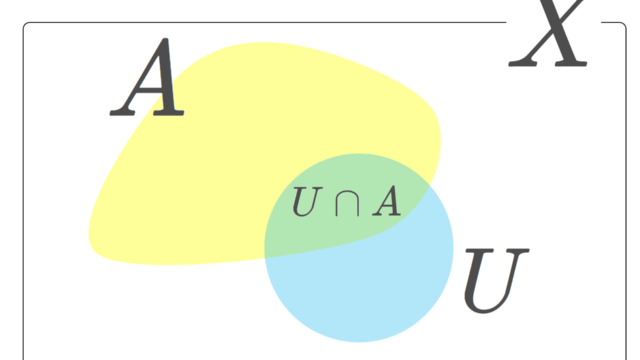 集合と位相
集合と位相