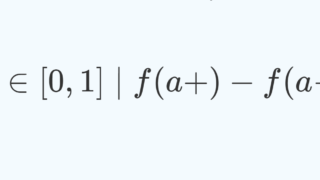確率論における,累積分布関数(もしくは単に分布関数ともいう)は, F(x) = P(X\le x ) と定義されます。これについて,その例と性質7つを紹介します。
累積分布関数(分布関数)の定義
まずはもう一度,定義をちゃんと述べておきましょう。
定義(累積分布関数;分布関数)
X を実数値確率変数とする。このとき,
\color{red} F(x) = P(X\le x) = P(X\in (-\infty, x] )
を累積分布関数 (cumulative distribution function; CDF) または単に分布関数 (distribution function) という。
測度論的確率論では,単に「分布関数」ということの方が多いです。
もし X が連続型確率分布であり,その確率密度関数を p(x) とすると,
F(x) = P(X\in (-\infty, x] ) = \int_{-\infty}^x p(x)\, dxすなわち,確率密度関数の不定積分になるわけですね。
累積分布関数(分布関数)の例
例を3つ挙げましょう。
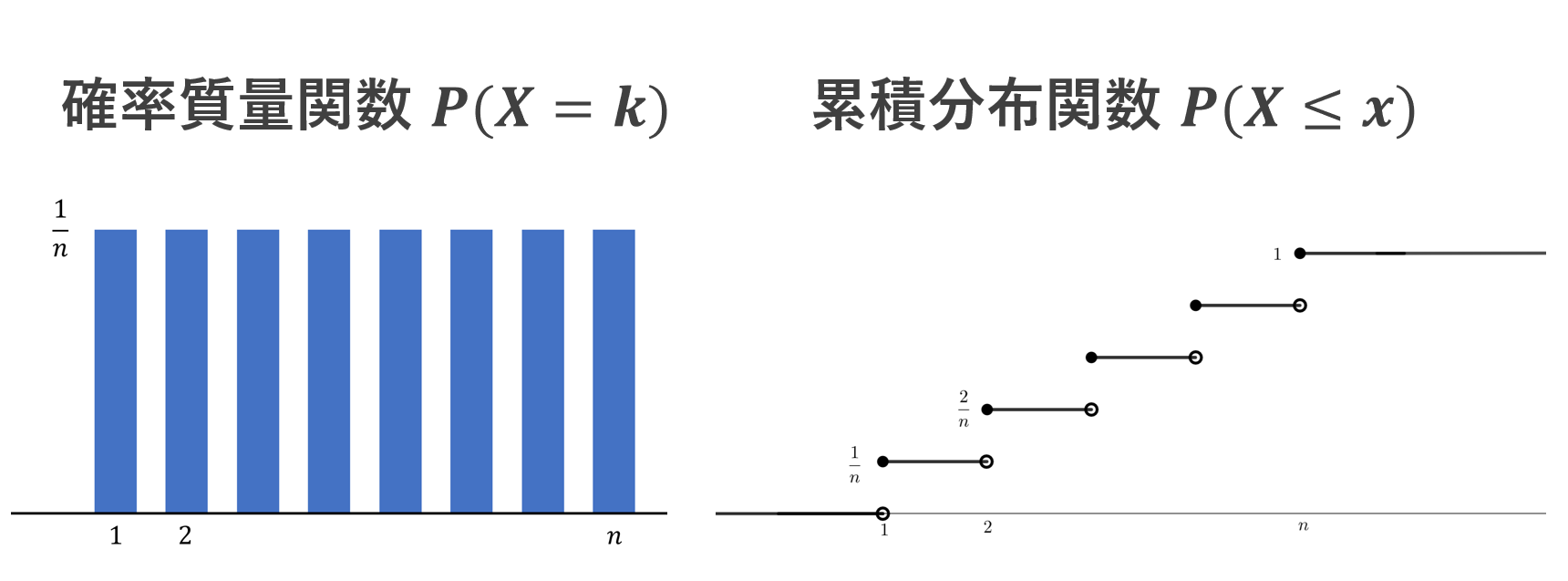
離散一様分布の累積分布関数
P(X=k) = \frac{1}{n}\quad (k=1,2,\ldots, n )
となる離散一様分布を考えましょう。これについて,累積分布関数は,
とかけます。ただし,\lfloor x \rfloor は床関数(ガウス記号)を表します。図で描くと,以下の通りです。
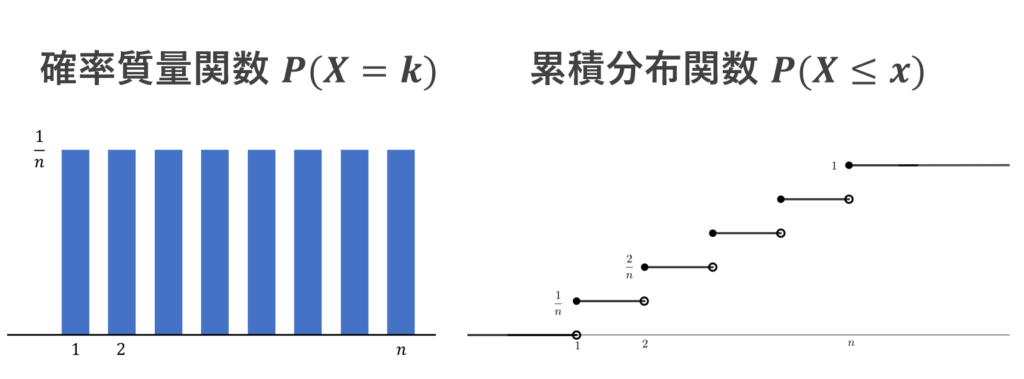
離散型の確率変数の場合は,累積分布関数は不連続な関数になります。
離散一様分布の詳細については,一様分布の定義と性質のわかりやすいまとめ~離散型・連続型~を参照してください。
連続一様分布の累積分布関数
確率密度関数が p(x) = \begin{dcases} \frac{1}{b-a} & a\le x \le b, \\ 0 & \text{otherwise} \end{dcases} となる連続一様分布を考えましょう。これについて,累積分布関数は,
F(x) = \int_{-\infty}^x p(x)\, dx = \begin{dcases} 0 & x\le a, \\ \frac{x-a}{b-a} &a\le x \le b, \\ 1 & b \le x \end{dcases}
となります。図で描くと,下のようになります。
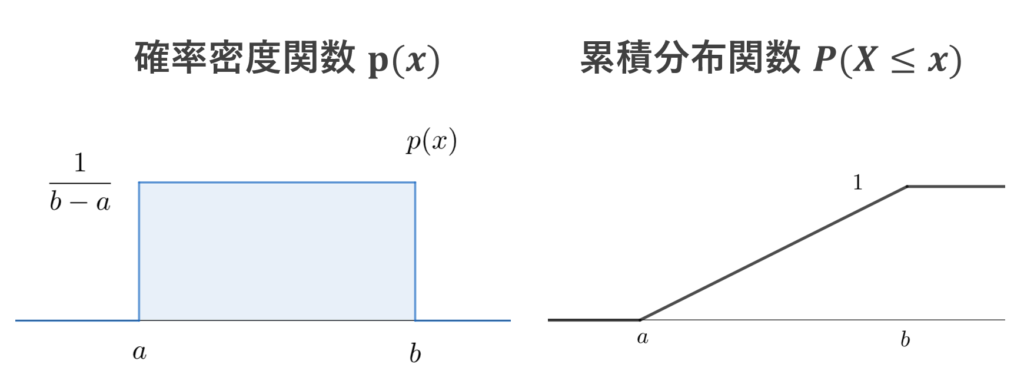
連続一様分布の詳細については,一様分布の定義と性質のわかりやすいまとめ~離散型・連続型~を確認してください。
指数分布の累積分布関数
確率密度関数が p(x) = \begin{cases} \lambda e^{-\lambda x} & x\ge 0 , \\ 0 & x < 0 \end{cases} となる指数分布を考えましょう。これについて,累積分布関数は,
F(x) = \int_{-\infty}^x p(x)\, dx = \begin{cases} 0 & x< 0, \\ 1-e^{-\lambda x} & x \ge 0 \end{cases}
となります。グラフで描くと,以下のようになります。
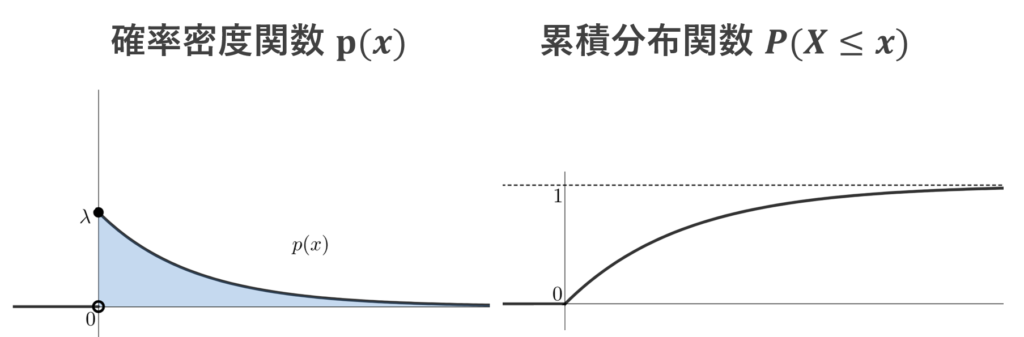
指数分布については,指数分布の定義と例と性質まとめで解説しています。
累積分布関数(分布関数)の性質7つ
さて,今回考える累積分布関数の性質7つを紹介しましょう。
定理(累積分布関数の性質)
F を累積分布関数とするとき,
- F は広義単調増加である。
- F(-\infty) = \lim_{x\to-\infty} F(x) =0 , \quad F(\infty)=\lim_{x\to\infty} F(x) =1.
- F は右連続である。
- F の不連続点は高々可算個である。
- 確率密度関数 p(x) が存在するとき, F は連続である。
- P(a<X\le b) = F(b) - F(a), \quad P(a\le X\le b ) = F(b)-F(a-) . ただし, F(a-) = \lim_{x\to a-} F(x) と定義する。
- P(X\ge 0) = 1 (すなわち F(0-)=0 )のとき, E[X] = \int_0^\infty (1-F(x))\, dx\in [0,\infty].
順番に考えていきましょう。
1. 累積分布関数が広義単調増加であること
これは, x< y とすると,
F(x) = P(X\le x) \le P(X\le y) = F(y)
なので,明らかでしょう。
2. F(-∞)=0, F(∞)=1 であること
2. F(-\infty) = \lim_{x\to-\infty} F(x) =0 , \quad F(\infty)=\lim_{x\to\infty} F(x) =1.
証明
X は実数値確率変数なので,
\begin{aligned}\lim_{x\to -\infty} F(x) &= \lim_{x\to -\infty} P(X\le x)\\ &= P(X\le -\infty) = 0 \end{aligned}
であり,
である。
証明終
3. 累積分布関数は右連続であること
3. F は右連続である。
証明
a< x としよう。このとき,
\begin{aligned} \lim_{x\to a+} F(x) &= \lim_{x\to a+} P(X\le x)\\&= P(X\le a) = F(a) \end{aligned}
であるから, F は右連続である。
証明終
4. 累積分布関数の不連続点が高々可算個であること
4. F の不連続点は高々可算個である。
これについては, F の単調性(性質1)から,「単調な関数の不連続点は高々可算個である」というFrodaの定理が適用できるため,従います。Frodaの定理については,以下の記事を参照してください。
5. 確率密度関数が存在するとき,累積分布関数が連続であること
5. 確率密度関数 p(x) が存在するとき, F は連続である。
これは,
F(x) = P(X\le x) = \int_{-\infty}^x p(y)\, dy
と積分表示できることから,明らかですね。
6. P(a<X≤b) = F(b)-F(a), P(a≤X≤b) = F(b)-F(a-)
6. P(a<X\le b) = F(b) - F(a), \quad P(a\le X\le b ) = F(b)-F(a-) . ただし, F(a-) = \lim_{x\to a-} F(x) と定義する。
証明
前半は
\begin{aligned} F(b)-F(a)&=P(X\le b)-P(X\le a) \\&= P(a<X\le b) \end{aligned}
より。後半について, x<a とすると,
であることから,
となって従う。
証明終
なお, F(x-) = P(X<x ) となることから,この関数は左連続になります。
7. 期待値の累積分布関数による表現
7. P(X\ge 0) = 1 (すなわち F(0-)=0 )のとき, E[X] = \int_0^\infty (1-F(x))\, dx\in [0,\infty].
これは,いわゆる部分積分公式と言えます。証明には,少し高度な知識が必要です。
なお,1- F が積分可能なことは, F の単調性と,「単調な関数は積分可能」であることから,大丈夫です(→ リーマン和による定積分の定義とリーマン積分可能・不可能な例)。
証明
確率 1 で X \ge 0 であることと, F が広義単調増加であること(性質1)から,
\begin{aligned} \int_0^\infty (1-F(x))\, dx &= \int_0^\infty \int_x^\infty dF(y)\, dx \\ &= \int_0^\infty \int_0^y dx\, dF(y) \\ &= \int_0^\infty y \,dF(y) \\ &= E[X] .\end{aligned}
ただし, dF(y) はリーマン-スティルチェス積分である。
証明終
全ての性質が証明できましたね。