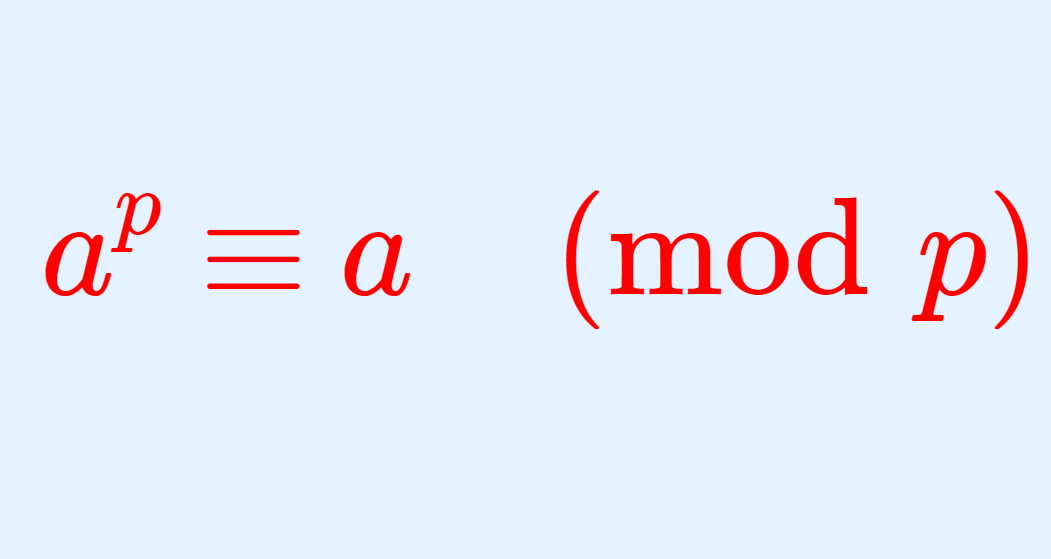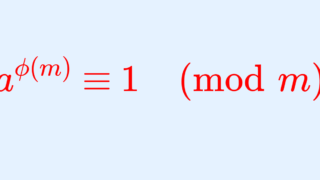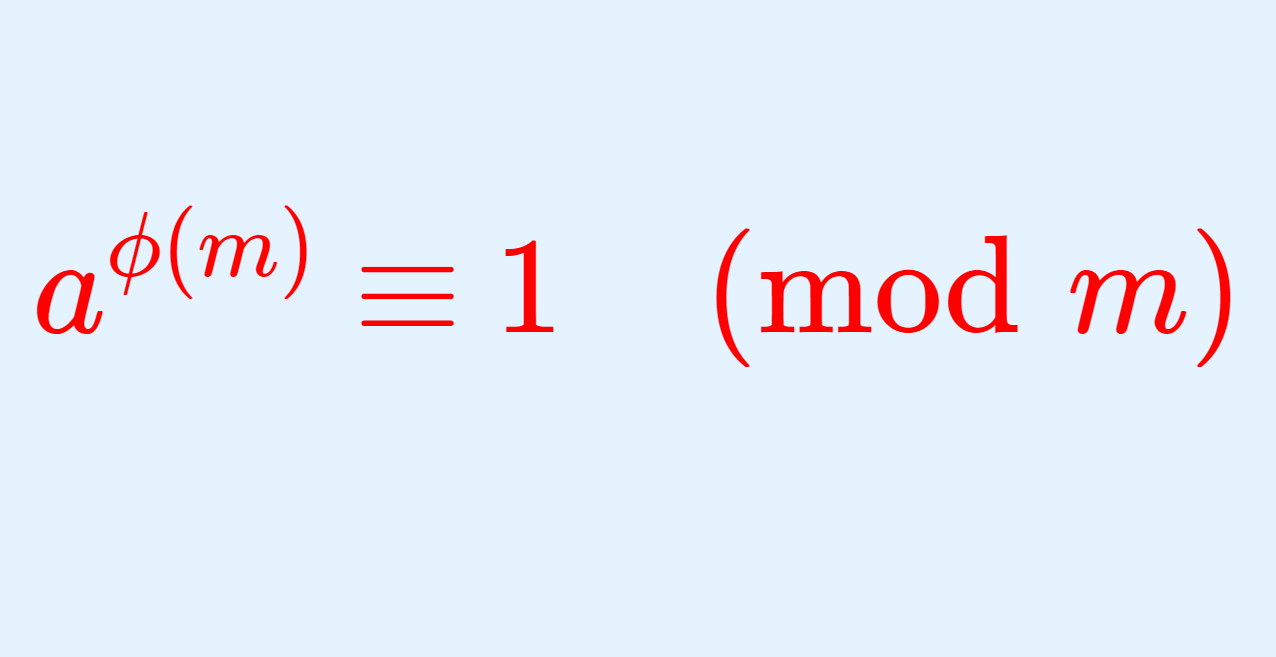フェルマーの小定理とは,整数の剰余に関する有名な定理です。これについて,その主張と証明3通りの解説をしましょう。最後には,その一般化も紹介します。
フェルマーの小定理とは
フェルマーの小定理 (Fermat’s little theorem)
p を素数, a を p と互いに素な整数とする。このとき,
\large\color{red} a^{p-1}\equiv 1 \pmod p
が成立する。また,任意の整数 a に対して,
が成立する。
かなり有名な定理です。上の2つの主張のうち,片方を示せば,もう片方も簡単に示せます。
実際,前半が示せれば,a が p と互いに素のときは両辺 a をかけるだけで,そうでないときは a^p\equiv a \equiv 0 で後半が言えますね。また,後半が示せれば, a が p と互いに素のときは両辺 a で割り算できるため,前半が従います。
フェルマーの小定理は,RSA暗号にも用いられている重要な理論です。
注意ですが, p-1 は a^{n}\equiv 1 \pmod p をみたす整数 n \ge 1 の中で,最小のものとは限りません。
フェルマーの小定理の3通りの証明
さて,フェルマーの小定理の証明について,
- a,\dots, (p-1)a を p で割った余りが異なることを利用した証明
- 数学的帰納法を用いた証明
- 群論の知識を用いた専門的な証明
の順に行っていきます。
1. a,…,(p-1)aをpで割った余りは異なることを利用した証明
証明
a,2a,3a,\dots, (p-1)a を p で割った余りはどの2つも異なることを示そう。整数 1\le i\le j\le p-1 に対し,
ja - ia = (j-i)a
であり, a は p と互いに素であることと, 0\le j-i\le p-2 であることから, ia\equiv ja\pmod p である必要十分条件は i=j である。従って,赤字は示せた。
このことより, a,2a,\dots, (p-1)a を p で割った余りは 1,2,\dots, p-1 が1回ずつ現れる。よって \mod p で
a\cdot 2a \cdots(p-1)a \equiv 1\cdot 2\cdots (p-1)
となる。すなわち, a^{p-1}(p-1)! \equiv (p-1)!\pmod p である。 (p-1)! と p は互いに素なので,両辺 (p-1)! で割ることができて(後述)
が求まる。
証明終
最後に両辺 (n-1)! で割っていますね。これを説明すると, (p-1)! \,(a^{p-1}-1) が p で割れることから, a^{p-1}-1 が p で割れることになるため, a^{p-1}\equiv 1 \pmod p というわけです。
非常に鮮やかで,高校生でも理解できる証明ですね。
2. 数学的帰納法を用いた証明
さて,整数論に明るくない場合は,次の証明の方が分かりやすいかもしれません。 a に関する数学的帰納法を用います。
証明
a\equiv a+np \pmod p (n は整数) なので,正の整数 a に対してのみ定理を証明すればよい。
1^{p}\equiv 1 \pmod p は明らか。正の整数 a について a^p \equiv a \pmod p が成り立っていると仮定する。このとき,二項定理より
\begin{aligned}(a+1)^p - (a+1) &= \sum_{n=0}^p {}_p\mathrm{C}_n a^n -(a+1) \\ &= \sum_{n=1}^{p-1} {}_p\mathrm{C}_n a^n +( a^p - a)\end{aligned}
である。ここで, 1\le n\le p-1 のときは, {}_p\mathrm{C}_n は p の倍数である。これと帰納法の仮定より,
である。ゆえに (a+1)^p \equiv a+1 \pmod p なので,証明が終わる。
証明終
地道に考える証明ですね。
3. 群論におけるラグランジュの定理を用いた専門的な証明
最後に,群論を用いた専門的な証明を行います。ここだけは,少しだけ代数の専門的な知識が必要です。
証明
有限体 \mathbb{Z}/p\mathbb{Z} の乗法群 (\mathbb{Z}/p\mathbb{Z})^{\times} の位数は p-1 である。
ラグランジュの定理より,元 a\in (\mathbb{Z}/p\mathbb{Z})^{\times} の位数 d は,群の位数の約数であるから, p-1= d m ( m は正の整数) とかける。従って,
a^{p-1} \equiv a^{dm}\equiv 1^m \equiv 1 \pmod p
を得る。
証明終
スリムな証明ですね。
フェルマーの小定理の一般化
フェルマーの小定理は,さらなる一般化が知られています。これについて,主張を紹介しましょう。
オイラーの定理 (Euler’s theorem)
\phi(n) を, 1,2,\dots, n-1 のうち, n と互いに素なものの個数とする(オイラーの \phi 関数という)。
m\ge 2 を整数, a を m と互いに素な整数とする。このとき,
\large\color{red} a^{\phi(m)} \equiv 1 \pmod m
である。
素数 p を,より一般の整数 m\ge 2 に拡張しています。 m=p のときは, \phi(p)=p-1 ですから,確かに一般化になっていますね。
これについては,以下で詳しく解説しています。