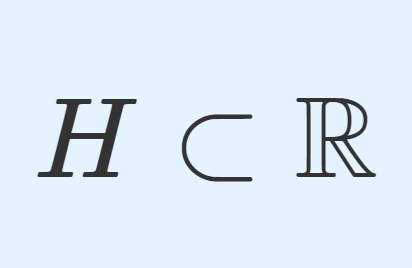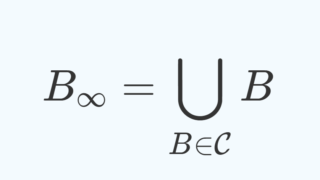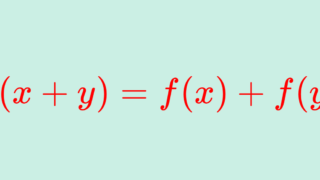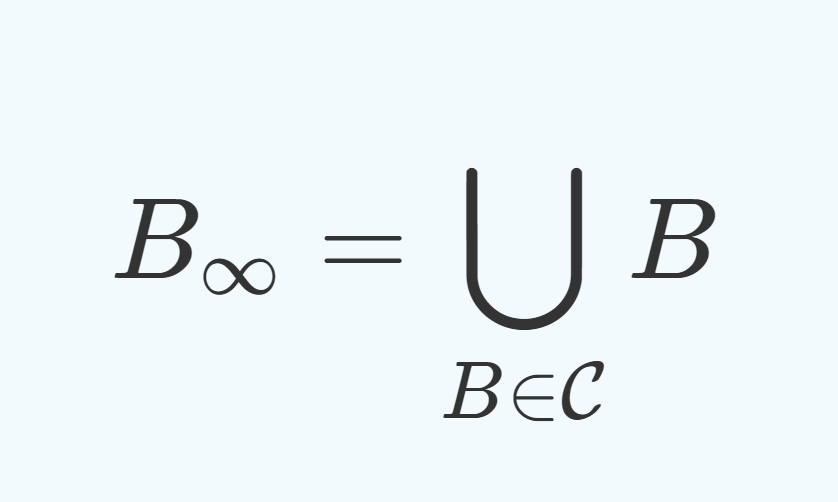ハメル基底とは,実数を有理数上のベクトル空間とみなしたときの基底のことを言います。ハメル基底についてその定義と濃度,関連する話題を紹介しましょう。
ハメル基底とは
\R は実数全体の集合で,\mathbb{Q} は有理数全体の集合です。
定義(ハメル基底)
\mathbb{R} を \mathbb{Q} 上のベクトル空間とみる。このベクトル空間における基底 H\subset\R をハメル基底 (Hamel basis) という。すなわち,
- 任意の有限個の q_1,q_2,\dots, q_n \in \mathbb{Q},\, h_1,h_2,\dots, h_n \in H に対し,
\begin{aligned} &q_1h_1+q_2h_2+\cdots + q_nh_n=0\\ &\implies q_1=q_2=\cdots = q_n=0\end{aligned} - 任意の x\in \R に対し,ある有限個の q_1,q_2,\dots, q_m \in \mathbb{Q},\,h_1,h_2,\dots, h_m \in H が存在して,
x=q_1h_1+q_2h_2+\cdots + q_mh_m
とできる H のことをハメル基底 (Hamel basis) という。
選択公理を認めることで,任意のベクトル空間に基底が存在することが分かっているため,ハメル基底は存在するといえます。基底の存在は以下で証明しています。
なお,あくまで選択公理を用いて存在が分かるというものですから,具体的な構成が分かるわけではありません。具体的な構成が分かれば,そもそも選択公理はいらないわけですが,今はそういうわけではありません。また,ハメル基底は一意的ではありません。名前はついていますが,一つに確定しているものではありません。
ハメル基底は具体的な構成が分かっているわけではありませんが,カントール集合の部分集合として取れることが知られています([1, Corollary 9.3.3])。
ハメル基底の濃度
定理(ハメル基底の濃度)
ハメル基底 H\subset \R は連続体濃度を持つ。
連続体濃度とは, \R と同じ濃度です。簡単に証明しておきましょう。[1] の Lemma 4.2.2 を参考にしています。
証明
可算濃度を |\mathbb{N}| =|\mathbb{Q}|= \aleph_0,連続体濃度を |\mathbb{R}|=\aleph と書くことにし,さらに H の濃度を |H|=\mathfrak{m} とする。
H は明らかに無限集合であることと, H\subset \R より,\aleph_0\le \mathfrak{m}\le \aleph である。
\mathcal{H}_n = \{ H'\subset H\mid \# H'=n\}
とし, \mathcal{H}=\bigcup_{n=1}^\infty \mathcal{H}_n とする。このとき, |\mathcal{H}_n |\le \mathfrak{m}^n=\mathfrak{m} であるから, |\mathcal{H}|\le \aleph_0\mathfrak{m}=\mathfrak{m} である。ここで,
であった(Spanは H' の元の \mathbb{Q} 上線形結合を指す→Spanの意味とは【線形結合】)。
\# H'=n とすると, |\operatorname{Span}_\mathbb{Q} H'| = \aleph_0^n =\aleph_0 であるから,(1) 式より,
\aleph\le \mathfrak{m}\aleph_0=\mathfrak{m}.
以上から, \mathfrak{m}\le \aleph\le \mathfrak{m} となっているから, \mathfrak{m}=\aleph である。
証明終
ハメル基底と関連する話題
ハメル基底と関連する話題としては,コーシーの関数方程式 (Cauchy’s functional equation; 加法的関数, additive function)
\color{red} f(x+y)=f(x)+f(y)
が有名でしょう。これをみたす関数 f\colon \R\to\R は,ハメル基底を認めれば無数にあります。具体的には, h_0\in H を一つ選びだしてきて,
と定めると,任意の r\in \R に対して, h_1,\dots, h_n \in H,\; q_0,q_1,\dots, q_n\in \mathbb{Q} として
と表したとき, f(r)=q_0 とすると,これは f(x+y)=f(x)+f(y) をみたしますね。
他にも, g\colon H\to \R を任意に定めたとき, f|_H = g となる( f の H への制限が g と一致する) g の拡張 f\colon \R\to\R のうち,コーシーの関数方程式をみたすものを一つ構成することが可能です。
コーシーの関数方程式に関しては,以下で詳しく解説しています。