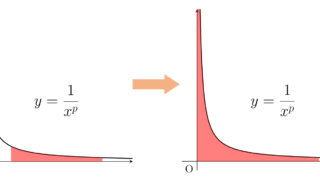
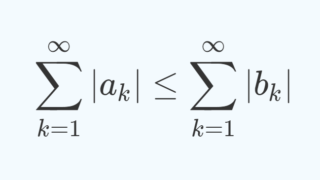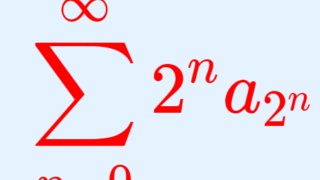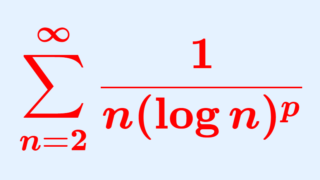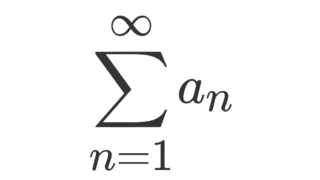積分を用いた， a_n \ge 0 である正項級数 \sum_{n=1}^\infty a_n の収束判定法を考え，それを用いて \sum_{n=1}^\infty 1/n^p, \,\, p> 0 の収束・発散について解説します。
広義積分による収束判定法
定理（広義積分による収束判定法; integral test）
\{ a_n \} を a_n \ge 0 \,\,(n\ge 1 ) とする。もし， f(n) = a_n となる単調減少な関数 f\colon [1, \infty) \to [0,\infty) が存在すれば，
\displaystyle\sum_{n=1}^\infty a_n の収束・発散は，広義積分 \displaystyle\int_1^\infty f(x) \, dx の収束・発散と一致する。
これを証明していきましょう。
広義積分については，以下の記事で解説しています。
広義積分による収束判定法の証明
証明
k \ge 2 に対して，
\int_{k}^{k+1} f(x) \, dx \le a_k \le \int_{k-1}^k f(x) \, dx
であるから，各辺 \sum_{k=2}^n をとると，
である。どの辺も n に関して単調増加のため，n\to\infty とすれば収束または \infty に発散することに注意しよう。これを踏まえて， n\to\infty とすれば， \infty の意味も含めて
f は単調減少より，\int_1^2 f(x)\, dx \le a_1 < \infty であり，よって \sum_{n=1}^\infty a_n の収束・発散は， \int_1^\infty f(x) \, dx の収束・発散と一致する。
証明終
図で描くと，以下の2つの収束評価を用いています。
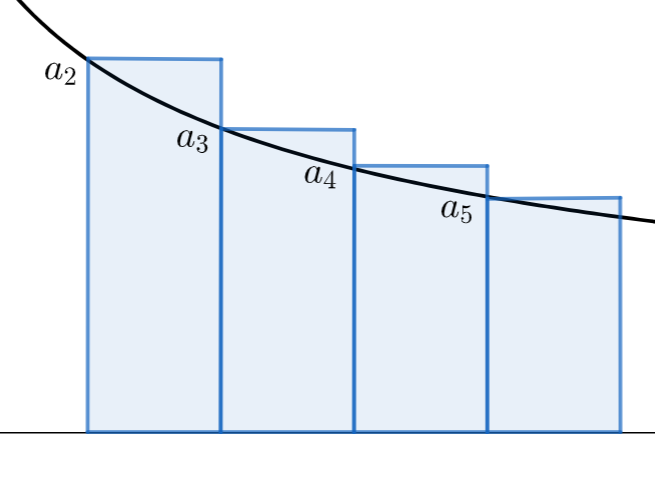
これは，級数を積分で下から評価した図になります。
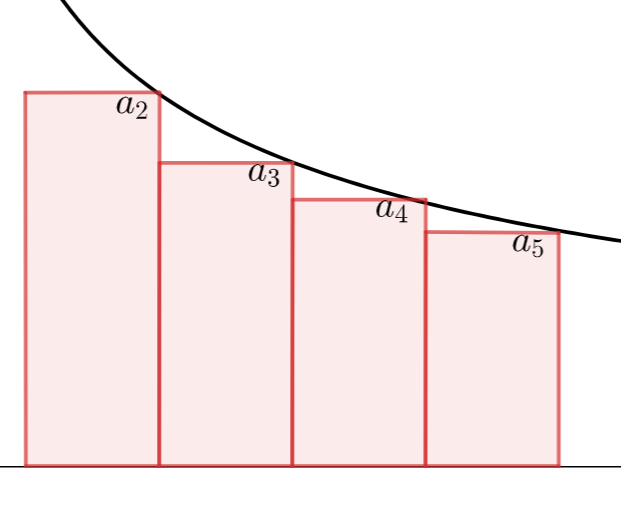
これは，級数を積分で上から評価した図になります。
a_2, a_3, a_4, a_5 に関わる部分だけ，両方を描画してみましょう。
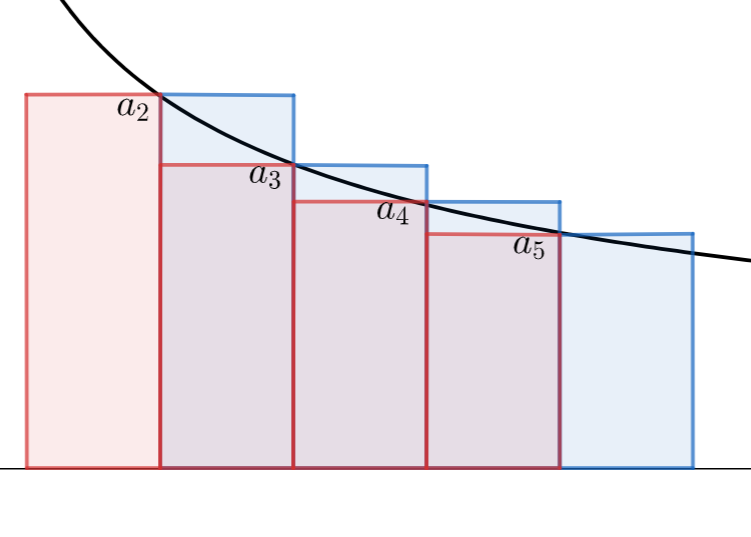
これが，上下から挟むような評価になっているわけです。
なお，証明において不等式で評価して，級数の収束・発展を判定していることから，これは比較判定法の一種だと言えます。
比較判定法については，以下の記事を参照してください。
1/n^pの和の収束・発散
これを用いれば，以下の定理が成立します。これも覚えておくとよいでしょう。
定理（1/n^p の和の収束・発散）
\color{red} \sum_{n=1}^\infty \frac{1}{n^p} \begin{cases} = \infty & 0 < p \le 1, \\ < \infty & p > 1 \end{cases}
すなわち， 0 < p \le 1 のとき発散， p > 1 のとき収束する。
証明
前の定理より，これの収束・発散は， \int_1^\infty 1/x^p \, dx の収束・発散に一致する。これと，
\int_1^x \frac{1}{y^p} \, dy = \begin{cases} \frac{1}{1-p}(x^{1-p} - 1) \to \infty & p < 1, \\ \log x \to \infty & p = 1, \\ \frac{1}{p-1} (1 - \frac{1}{x^{p-1}}) \to \frac{1}{p-1} & p > 1 \end{cases}
(n\to\infty) であることから従う。
証明終
なお，この収束・発散については，積分を用いずとも，Cauchy Condensation Test を用いて求めることも可能です。以下で解説しています。
類似の話題
同じく，広義積分による収束判定法によって証明される定理を述べましょう。
定理（ 1/n\log n 型の級数の収束・発散）
{ \sum_{n=2}^\infty \frac{1}{n(\log n)^p } }
は，
- {0 \le p \le 1} のとき発散
- {p > 1} のとき収束
する。
これについては，以下で解説しています。
