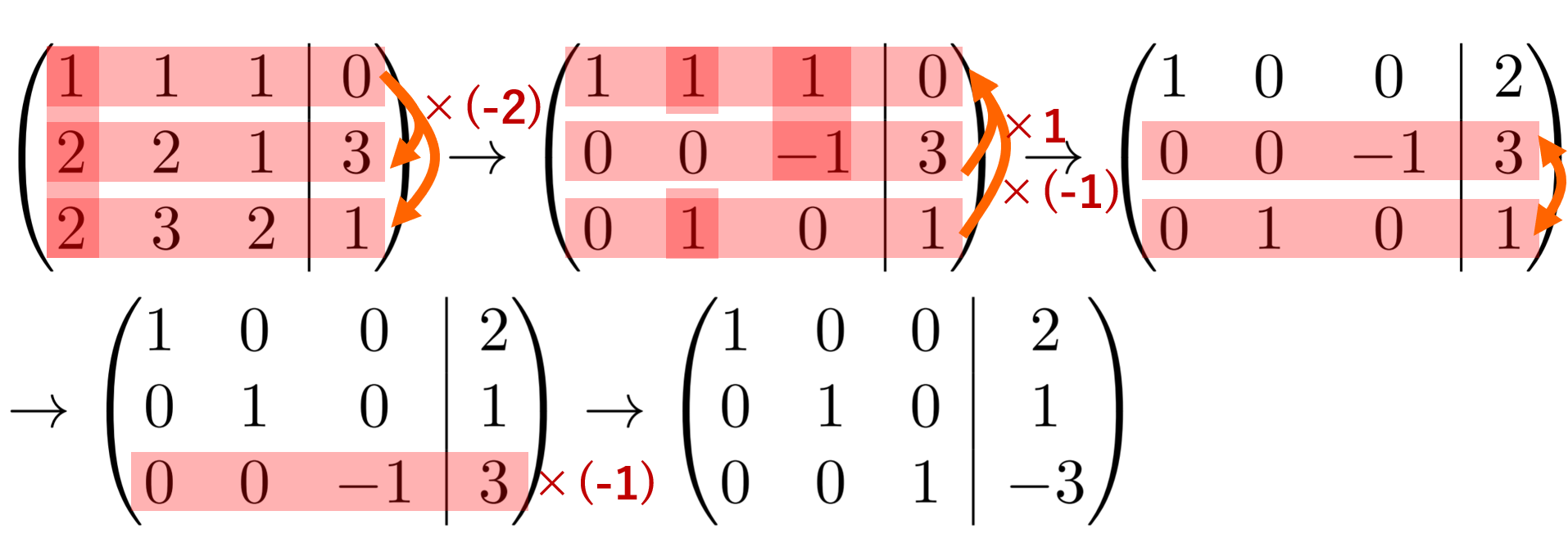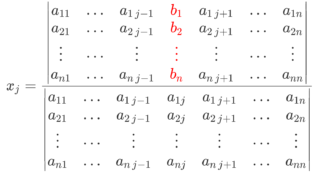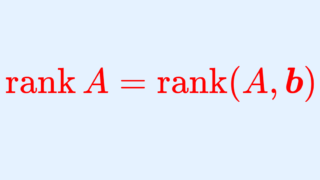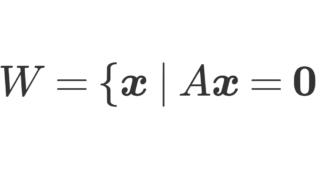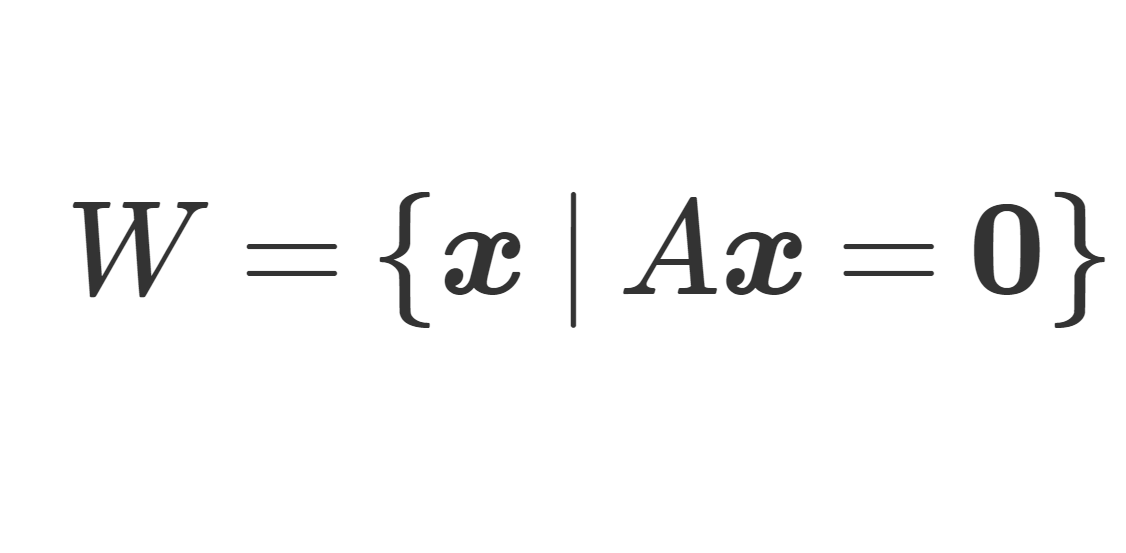行列で連立一次方程式を解く方法～計算の手順～

連立一次方程式は，行列の行基本変形による「ガウスの消去法(掃き出し法)」と呼ばれるものを用いて，比較的簡単に解くことができます。

これについて，具体的な計算手順を分かりやすく解説し，例題も交えながら確認していきましょう。

連立一次方程式の行列を用いた解法
連立一次方程式を解く例題
連立一次方程式のその他の解法
1. 【Aが正則のとき】逆行列を計算する方法
2. 【Aが正則のとき】クラメルの公式
連立一次方程式と行列に関する記事

連立一次方程式の行列を用いた解法

早速，解法の手順を解説しましょう。まずは，連立一次方程式を行列で表しましょう。

1. 連立一次方程式を行列で表す

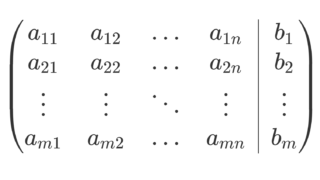
連立一次方程式

\begin{cases} a_{11}x_1+a_{12}x_2+\cdots + a_{1n}x_n = b_1 \\ a_{21}x_1+a_{22}x_2+\cdots + a_{2n}x_n = b_2 \\ \ldots \\ a_{m1}x_1+a_{m2}x_2+\cdots + a_{mn}x_n = b_m \end{cases}

は，行列を用いて表すと

\begin{pmatrix} a_{11} & a_{12} &\dots & a_{1n} \\ a_{21} & a_{22} &\dots & a_{2n} \\ \vdots & \vdots &\ddots & \vdots \\ a_{m1} & a_{m2}& \dots & a_{mn} \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} =\begin{pmatrix} b_1 \\b_2\\ \vdots \\ b_m \end{pmatrix}

とかけます。この式に対応して， $A\boldsymbol{x} = \boldsymbol{b}$ とかくことにしましょう。このときの $A$ を係数行列， $A$ と $\boldsymbol{b}$ を合体させた $(A,\boldsymbol{b})$ を拡大係数行列といいます。詳しくは，以下で解説しています。

これにより，連立一次方程式を行列を表すことができました。これを用いて，連立一次方程式を解くことを考えましょう。

2. ガウスの消去法(掃き出し法)による解の導出

拡大係数行列 $(A, \boldsymbol{b})$ を用いて，連立一次方程式を解きましょう。解き方は，行基本変形のみを用いて， $A$ を簡約化するように， $(A, \boldsymbol{b})$ を変形していきます。

「行基本変形」とは，以下の3つの変形のことを言います。

ある行の $c$ 倍を他の行に加えること
2つの行を入れ替えること
ある行を $c \ne 0$ 倍すること

詳しくは，行列の基本変形についてわかりやすく図解するで解説しています。

「行列の簡約化」とは以下のような，階段行列のうち，主成分が $1$ ，その上が $0$ であるような，RREF行列と呼ばれる行列に直すことです。

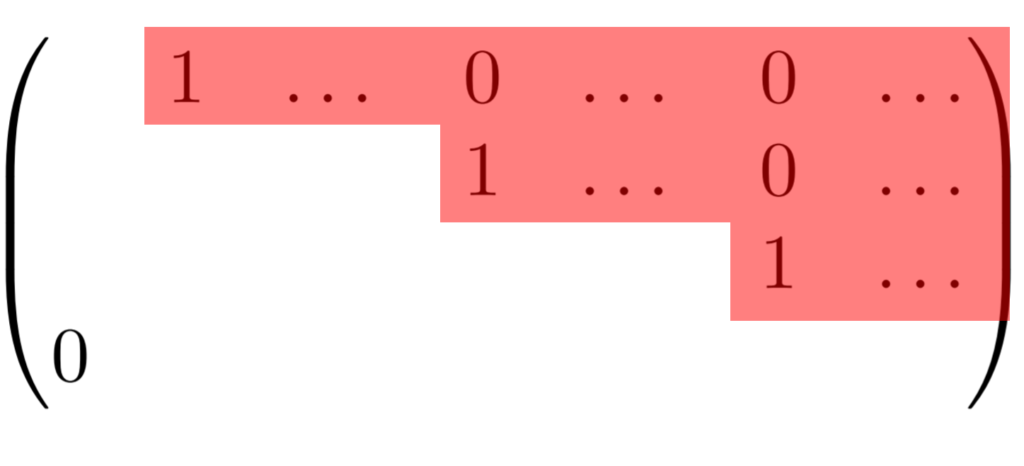
たとえば，単位行列は簡約された行列の1つです。詳しくは，【行列の簡約化】RREF行列(Reduced row echelon form)とはで解説しています。行基本変形では，単位行列に簡約化するつもりで変形していけばよいでしょう。

そして，行基本変形によって得た $(A', \boldsymbol{b'})$ を再び連立一次方程式 $A' \boldsymbol{x} = \boldsymbol{b'}$ の形に戻して，それを解きます。

こうすることで， $A\boldsymbol{x}=\boldsymbol{b}$ を素直に解こうとするよりも，簡単に解けます。まとめておきましょう。

連立一次方程式の行列を用いた解き方

拡大係数行列 $(A,\boldsymbol{b})$ に対し， $A$ を簡約化するように行基本変形を繰り返す。
行基本変形後の $(A',\boldsymbol{b'})$ に対し， $A'\boldsymbol{x}=\boldsymbol{b'}$ を解く。

連立一次方程式が解ける原理

上の方法で，連立一次方程式が解ける原理を簡単に解説しておきましょう。行基本変形というのは，左から基本行列と呼ばれる行列をかけることに相当します。拡大係数行列について，左から行列をかけて

S(A,\boldsymbol{b}) = (SA, S\boldsymbol{b})

とすることと，連立一次方程式 $A\boldsymbol{x}=\boldsymbol{b}$ に左から行列をかけて

SA\boldsymbol{x} = S\boldsymbol{b}

はちょうど対応していますから， $SA$ ができるだけ簡単になるように簡約化することで，上手く解けるというわけです。

関連：行列の演算（和・定数倍・積）の定義と性質をわかりやすく丁寧に

連立一次方程式を解く例題

さて，ここから具体例を挙げていきましょう。

例題1.

$\begin{cases} x_1 + x_2 +x_3=0 \\ 2x_1+2x_2 + x_3 =3 \\ 2x_1+3x_2+2x_3=1\end{cases}$ を解け。

拡大係数行列 $(A, \boldsymbol{b})$ は

\left(\!\!\! \begin{array}{ccc|c} 1&1&1 &0\\ 2&2& 1&3 \\ 2&3&2&1\end{array}\!\!\!\right)

ですね。これの左側の部分 $A= \begin{pmatrix} 1&1&1 \\ 2&2&1 \\ 2& 3& 2\end{pmatrix}$ を簡約化するように，行基本変形を繰り返しましょう。

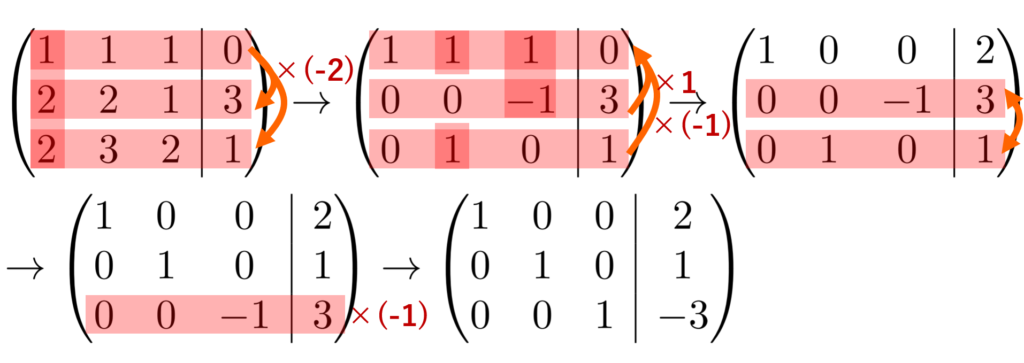
左の $A$ の部分は，簡約化すると単位行列になりましたね。基本変形後の行列を用いて，連立一次方程式に直すと，

\color{red} \begin{cases} x_1 = 2 \\ x_2 =1 \\ x_3 = -3 \end{cases}

となり，これは求める解そのものですね。

このように， $A$ の部分が単位行列に直せると，非常に簡単に解を導出することができます。

例題2.

$\begin{cases} x_1 + x_2 +x_3=3 \\ 2x_1+x_2 + x_3 =4 \\ 2x_1-x_2-x_3=0\end{cases}$ を解け。

拡大係数行列は $\left(\!\!\! \begin{array}{ccc|c} 1&1&1&3\\2&1&1&4\\2&-1&-1&0 \end{array} \!\!\!\right)$ ですね。行基本変形を繰り返すと

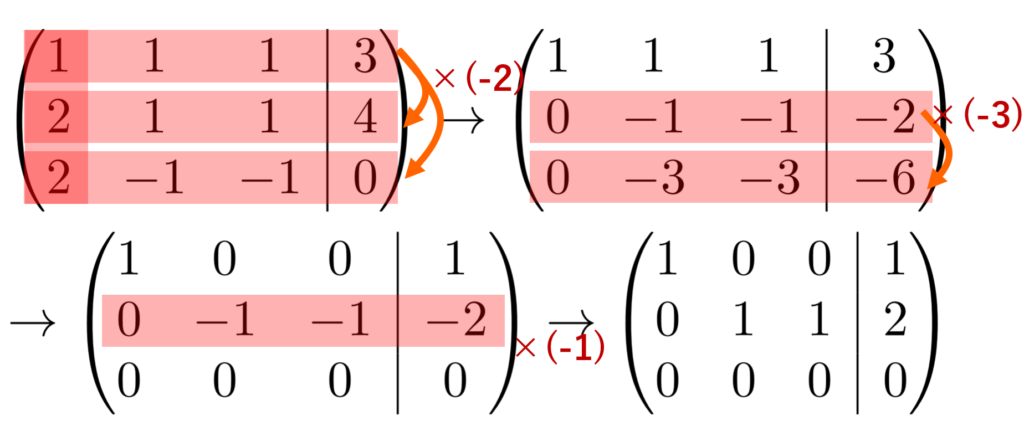
ですね。 $A= \begin{pmatrix} 1&1&1\\2&1&1\\ 2&-1&-1\end{pmatrix}$ を簡約化すると， $\begin{pmatrix} 1&0&0\\ 0&1&1 \\ 0&0&0\end{pmatrix}$ になりました。これを用いると，解くべき連立一次方程式は

\begin{cases} x_1 = 1 \\ x_2+x_3=2 \\ 0=0\end{cases}

ですから，たとえば， $x_2=a$ とおくと，求める実数解は

\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix} = \begin{pmatrix} 1 \\ a \\ 2-a \end{pmatrix}, \quad a\in\mathbb{R}

ですね。 $a\in\mathbb{R}$ とすれば実数解ですが， $a\in\mathbb{C}$ とすれば複素数解です。この辺は文脈に応じて使い分けてください。

この問題は，解に不定性がありましたね。連立一次方程式が3つあるように見えて，実は2つしかない(残り1つは2つから従う)ようなパターンには，このようなことになります。
この辺について深く知りたい場合は，連立一次方程式の基本解・特殊解と解空間の性質を参照してください。

例題3.

$\begin{cases} x_1 - x_2 +x_3=3 \\ x_2 + x_3 =0 \\ 2x_1+4x_2+8x_3=7\end{cases}$ を解け。

拡大係数行列は $\left(\!\!\! \begin{array}{ccc|c} 1&-1&1&3\\0&1&1&0\\2&4&8&7 \end{array} \!\!\!\right)$ ですね。行基本変形を繰り返すと，

ですから，解くべき連立一次方程式は

\begin{cases} x_1+2x_3 = 3 \\ x_2+x_3 = 0 \\ 0=1\end{cases}

になります。最後の $0=1$ はあり得ないですから，答えは解なしです。

このように，行基本変形後，左側が全て $0$ なのに，右側はそうなっていないような行が存在する場合は，「解なし」が答えになります。今回の場合，行基本変形後の最終行がそうなっていますから，解なしです。

ここで，行列の階数(ランク)について詳しければ， $\operatorname{rank}A = \operatorname{rank}(A,\boldsymbol{b})$ でないと解を持たないのではないか，と気づくかもしれません。実際その通りです。これについては連立一次方程式が解をもつ条件(行列)とその証明を参照してください。