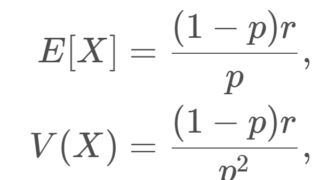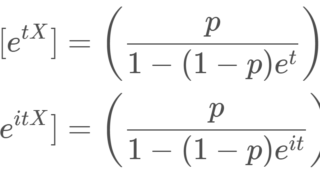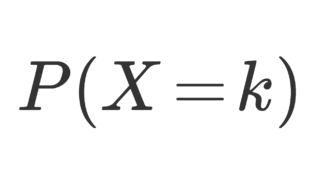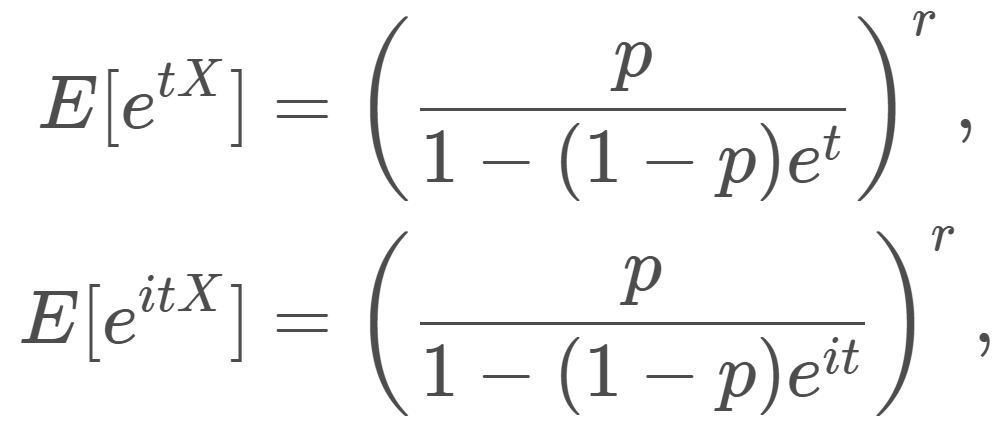コイン投げをしたときの成功回数を固定し,その成功回数に到達するまでの失敗回数を数える負の二項分布 NB(r, p) は, P(X=k) = {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k となる確率分布です。これについて,その定義と例と性質をまとめましょう。
負の二項分布の定義
定義(負の二項分布)
0<p<1, \, r\ge 1 を整数とする。確率変数 X が k = 0,1,2,\ldots に対し,
\color{red}\begin{aligned} P(X=k) &= {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k \\ &= {}_{k+r-1}\mathrm{C}_{r-1}\, p^r(1-p)^k \end{aligned}
となるとき, X はパラメータ (r, p) の負の二項分布 (negative binomial distribution) に従うという。本記事では,\color{red} X\sim NB(r,p) とかくことにする。
なお,重複組み合わせの記号を用いて,\color{red} {}_{r}\mathrm{H}_k\, p^r(1-p)^k とかいても同様です。本記事では,上の定義の第一等式 {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k のかたちを主に用います。
負の二項分布は,確率 p で表が出るコインについて, r 回表が出るまでのウラが出る回数を表したものです。
実際,「 r 回表が出るまでに, k 回ウラが出る確率」は,まず最初の r+k-1 回の試行の間に表が r-1 回,ウラが k 回出る確率が {}_{k+r-1}\mathrm{C}_k\, p^{r-1}(1-p)^{k} であり,最後の1回は表が出るので,確率 p で,最終的に
{}_{k+r-1}\mathrm{C}_k\, p^{r-1}(1-p)^{k} p = {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^{k}
になりますね。
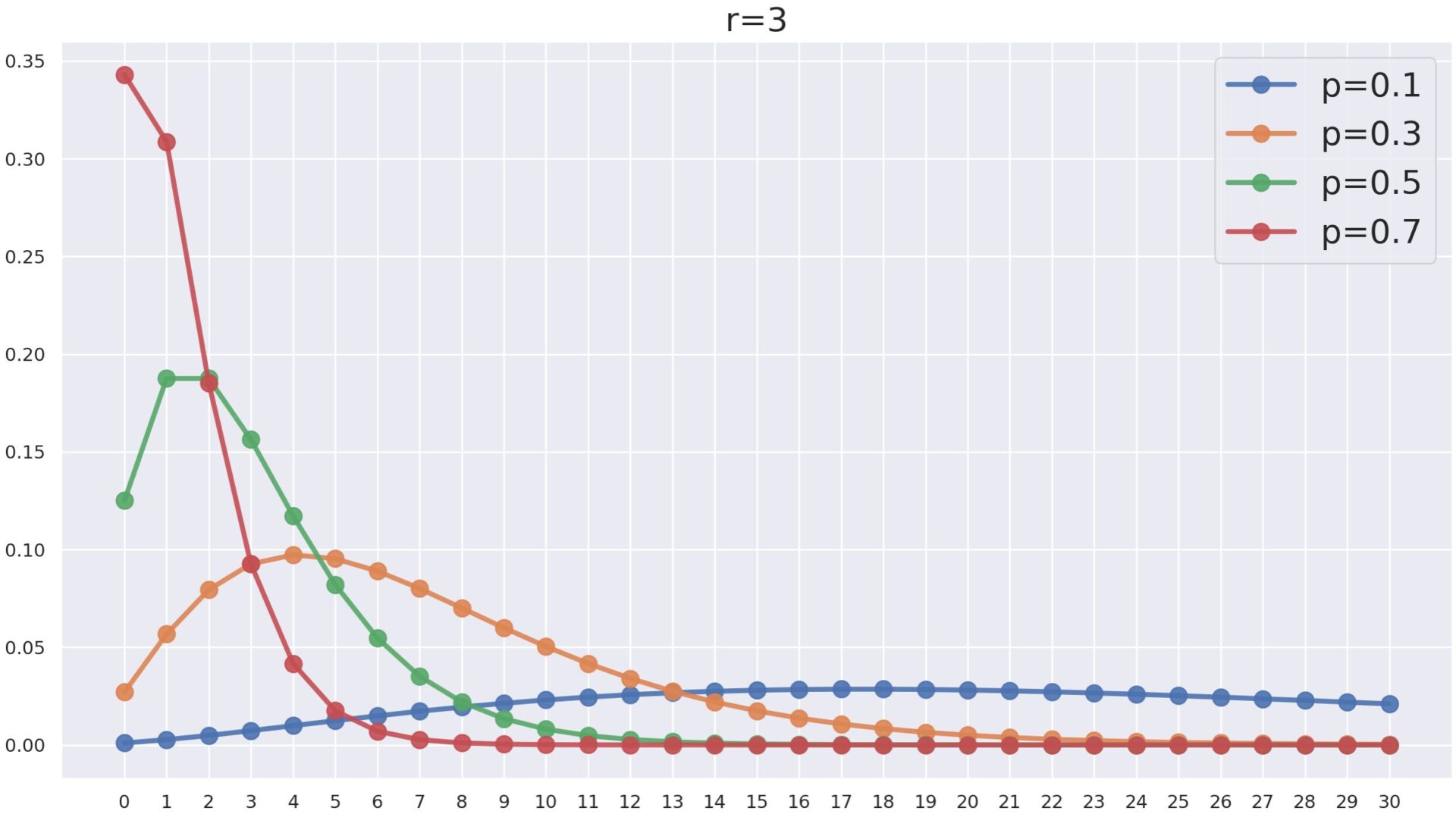
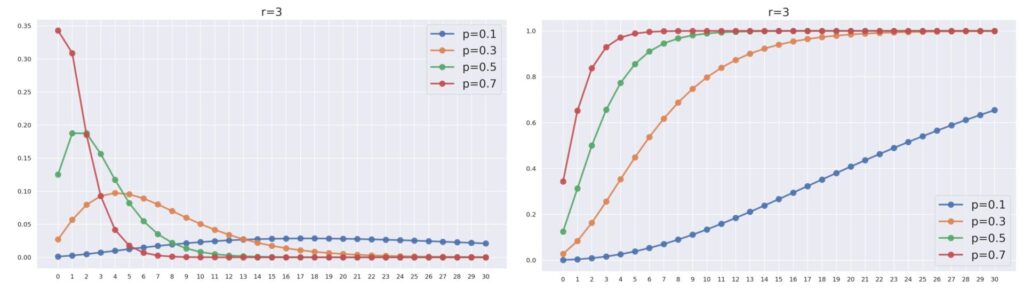
負の二項分布の確率関数のグラフ P(X=k) について, r= 3 とし, p を変化させたときの NB(3, p) は以下のようになります。
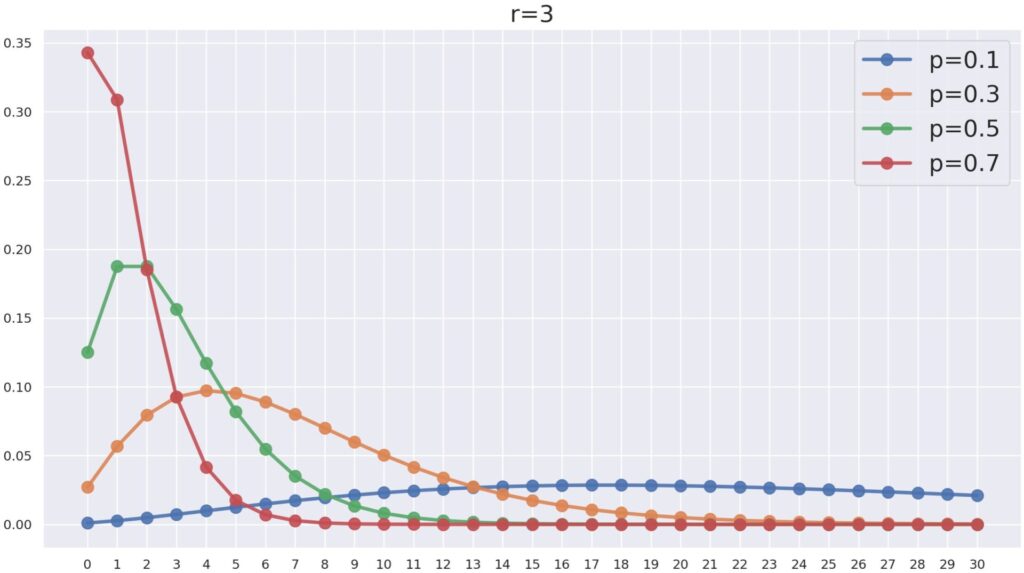
p が大きくなればなるほど,確率が k が小さな方に寄っていますね。 p が大きいと,失敗し辛くなりますから,同じ回数の成功を重ねるまでの失敗回数は減るわけですね。
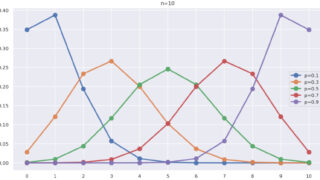
また,p=0.5 を固定し, r を変えたときの NB(r, 0.5) は以下のようになります。
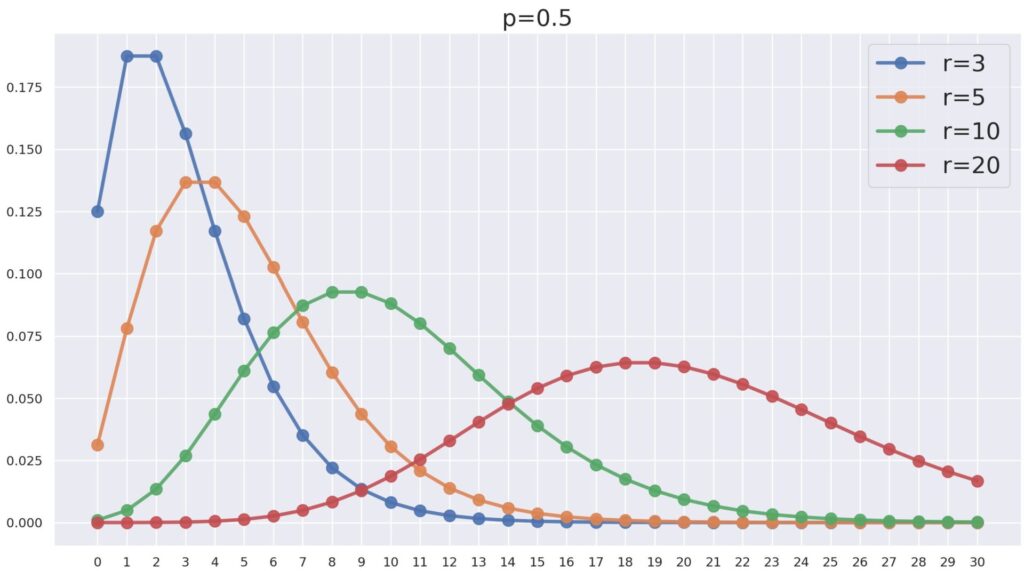
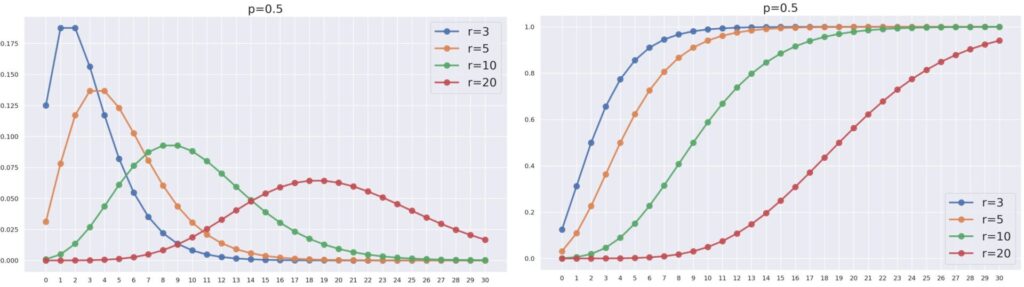
r が増えれば増えるほど,山が右に寄っていますね。これはある意味当たり前でしょう。
二項分布との違い
二項分布 B(n, p) との違いを押さえておきましょう。負の二項分布は,確率 p で表が出るコインについて, r 回ウラが出るまでの表が出る回数を表したもの であったのに対し,二項分布は,確率 p で表が出るコインを n 回投げたとき,表が出る回数を表したものでした。 コイン投げと思ったときの,両者の違いは,以下の通りです。
| コイン投げ | 二項分布 B(n,p) | 負の二項分布 NB(r, p) |
|---|---|---|
| 確率 | {}_n \mathrm{C}_k\, p^k (1-p)^{n-k} | {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k |
| 表が出る確率 | p (固定) | p (固定) |
| 試行回数の合計 | n (固定) | k+r |
| 失敗回数の合計 | n-k | k=0,1,2,\ldots |
| 成功回数の合計 | k=0,1,2,\ldots, n | r (固定) |
試行回数を固定しているのが,二項分布であり,成功回数を固定しているのが,負の二項分布なわけですね。
負の二項分布の性質まとめ
負の二項分布の性質をまとめます。
| 負の二項分布 NB(r,p) | |
|---|---|
| 確率 P(X=k) | {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k |
| 確率の型 | 離散型 |
| 幾何分布との関係 | NB(1,p)+1=\operatorname{Geo}(p) |
| 累積分布関数 F(x) = P(X\le x) | \begin{cases} 0 & x < 0, \\ \sum_{k=0}^{\lfloor x \rfloor} {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k & x\ge 0 \end{cases} |
| 期待値 E[X] | \dfrac{(1-p)r}{p} |
| 分散 V(X) | \dfrac{(1-p)r}{p^2} |
| 標準偏差 \sqrt{V(X)} | \dfrac{\sqrt{(1-p)r}}{p} |
| 積率母関数(モーメント母関数) E[e^{tX}] | \left(\dfrac{p}{1-(1-p)e^t}\right)^r,\; t<-\log (1-p) |
| 特性関数 E[e^{itX}] | \left(\dfrac{p}{1-(1-p)e^{it}}\right)^r,\; t\in\mathbb{R} |
順番に考えていきましょう。
負の二項分布と幾何分布との関係
Y\sim \operatorname{Geo}(1-p) は,確率変数 Y がパラメータ 1-p の幾何分布に従うことを指します。
定理(負の二項分布と幾何分布との関係)
X\sim NB(1, p), \; Y\sim \operatorname{Geo}(p) を独立とする。このとき,
\color{red} X +1 \stackrel{\mathrm{d}}{=} Y
が成立する。ただし, \stackrel{\mathrm{d}}{=} は分布の意味で等しいことを表す。
確率 p で表が出るコイン投げで考えましょう。負の二項分布で, r=1 としたものは,1 回表が出るまでにウラが出る回数ですね。一方で,幾何分布 \operatorname{Geo}(p) は, 1 回表が出るまでにサイコロを振る回数に相当しますから,ちょうど,上のような関係式が成立しているといえます。また,
\begin{aligned}&P(X=k) = {}_{k}\mathrm{C}_k\, p(1-p)^k \\ & = p(1-p)^k = P(Y=k+1)\end{aligned}
であることからも分かりますね。
負の二項分布の累積分布関数(分布関数)
負の二項分布の累積分布関数(分布関数)は,
\begin{aligned}F(x) &= P(X\le x) \\ &=\begin{cases}0 & x<0 \\ \sum_{k=0}^{\lfloor x \rfloor} P(X=k) & x\ge 0 \end{cases} \\ &= \begin{cases} 0 & x < 0, \\ \sum_{k=0}^{\lfloor x \rfloor} {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k & x\ge 0 \end{cases}\end{aligned}
となります。
r= 3 とし, p を変化させたときの NB(3, p) とその累積分布関数の関係は,以下のようになります。
また,p=0.5 を固定し, r を変えたときの NB(r, 0.5) とその累積分布関数の関係は,以下のようになります。
負の二項分布の期待値(平均)・分散・標準偏差
定理(負の二項分布の期待値(平均)・分散・標準偏差)
X\sim NB(r, p) とする。このとき, X の期待値(平均)・分散・標準偏差は
\color{red} \begin{aligned} E[X] &= \dfrac{(1-p)r}{p},\\ V(X)&= \dfrac{(1-p)r}{p^2},\\ \sqrt{V(X)}&= \dfrac{\sqrt{(1-p)r}}{p} \end{aligned}
である。
これについては,以下の記事で解説しています。
負の二項分布の積率母関数(モーメント母関数)・特性関数
定理(負の二項分布の積率母関数(モーメント母関数)・特性関数)
X\sim NB(r, p) とする。このとき, X の積率母関数(モーメント母関数)・特性関数は
\color{red} \begin{aligned} E[e^{tX}] &= \left(\dfrac{p}{1-(1-p)e^t}\right)^r,\quad t<-\log (1-p),\\ E[e^{itX}]&=\left(\dfrac{p}{1-(1-p)e^{it}}\right)^r,\quad t\in\mathbb{R} \end{aligned}
である。
これについては,以下で解説しましょう。