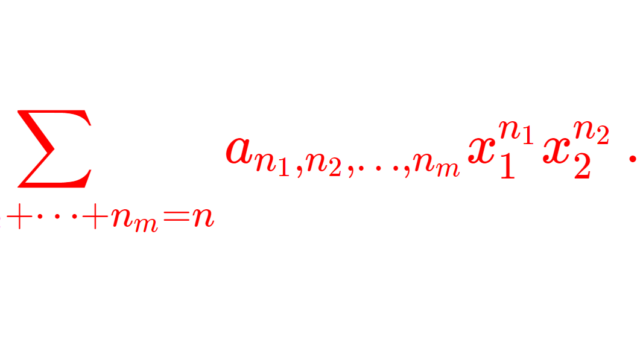 群・環・体
群・環・体 同次式(斉次式)とは
同次式(どうじしき)あるいは斉次式(せいじしき; homogeneous polynomial)とは,(多変数)多項式において,全ての項の次数が等しいようなものを言います。同次式(斉次式)について,定義と具体例,性質をまとめます。
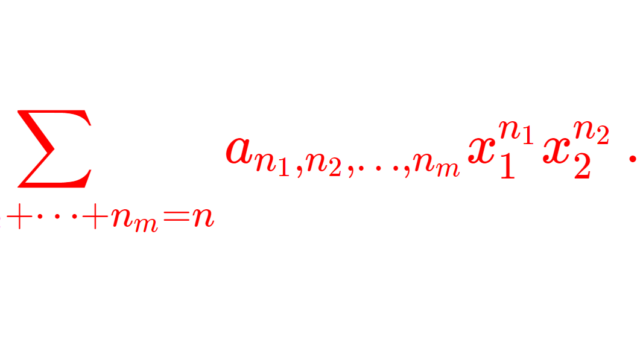 群・環・体
群・環・体  確率論
確率論  関数解析学
関数解析学 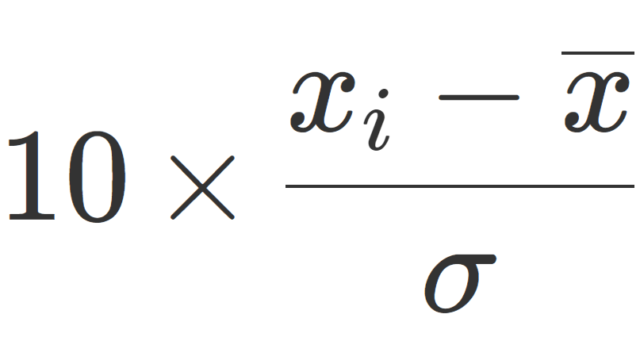 統計学
統計学 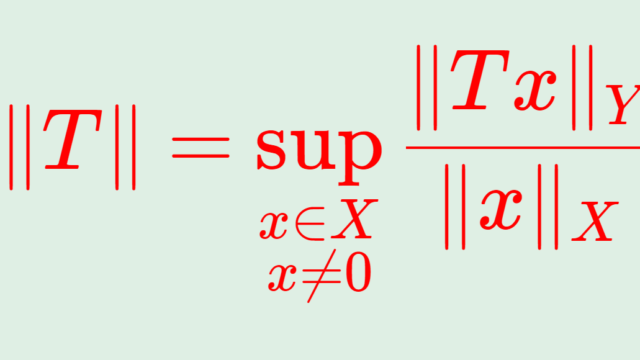 関数解析学
関数解析学 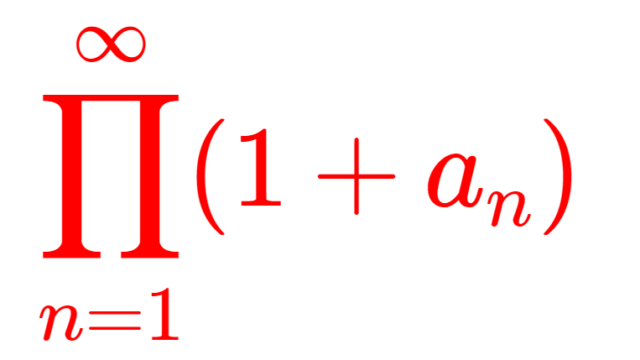 解析学(大学)その他
解析学(大学)その他 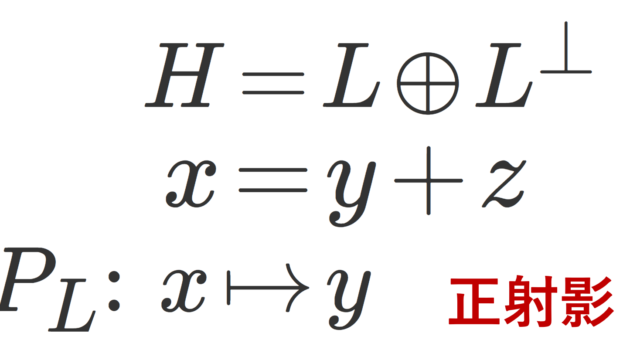 関数解析学
関数解析学 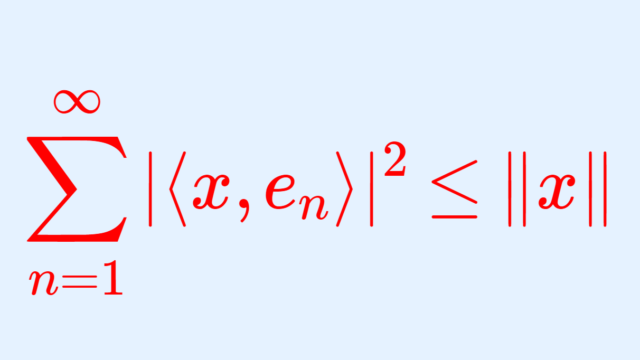 関数解析学
関数解析学 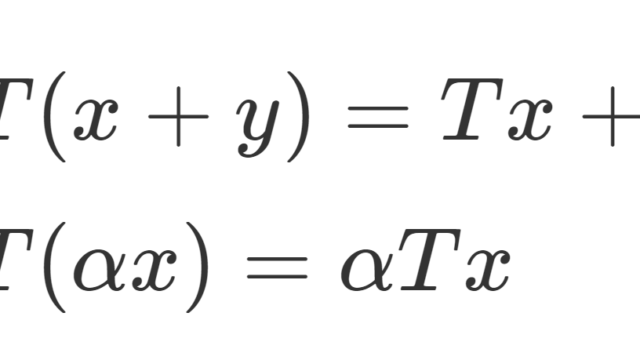 関数解析学
関数解析学  関数解析学
関数解析学