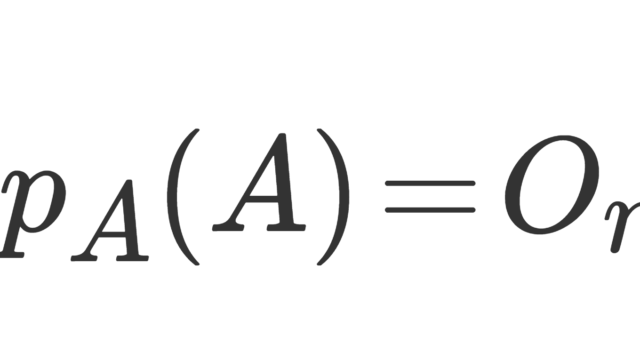 線形代数学
線形代数学 ケーリーハミルトンの定理とその厳密な証明をわかりやすく
ケーリーハミルトンの定理(Cayley-Hamilton theorem)とは,正方行列Aの固有多項式p_A(λ)に対し,p_A(A)=O_nとなる定理です。今回は,最小多項式の基にもなっているケーリーハミルトンの定理について紹介します。
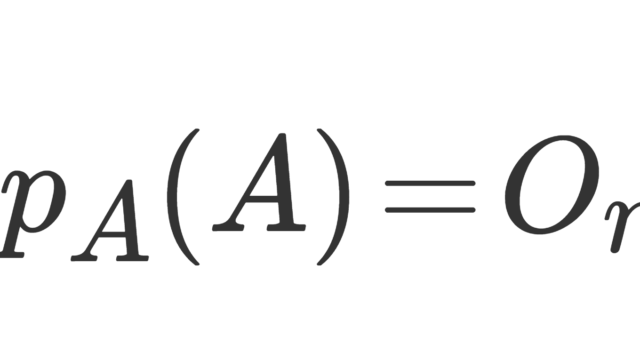 線形代数学
線形代数学 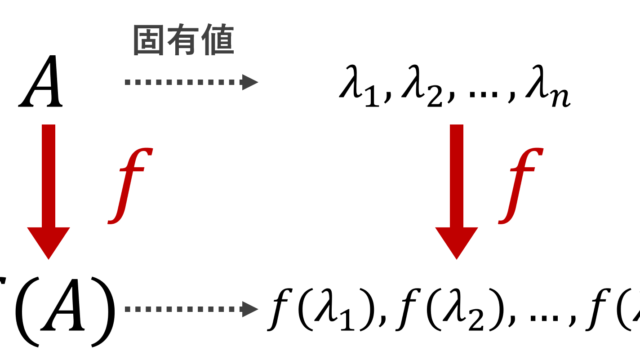 線形代数学
線形代数学 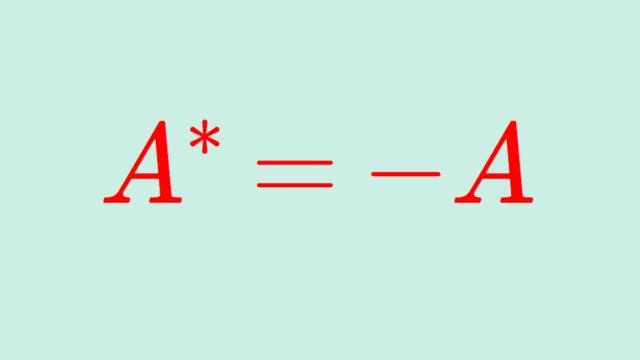 線形代数学
線形代数学  線形代数学
線形代数学 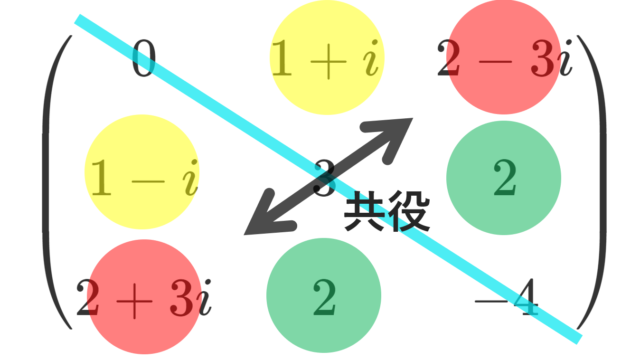 線形代数学
線形代数学 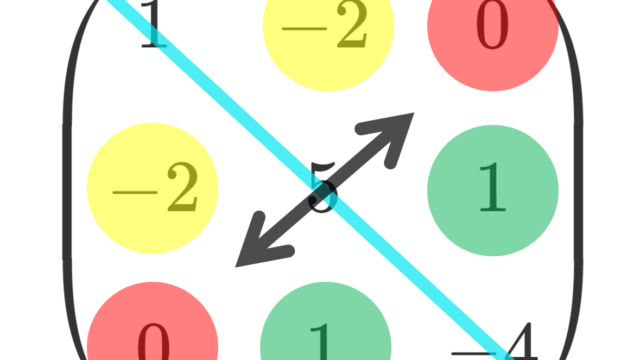 線形代数学
線形代数学 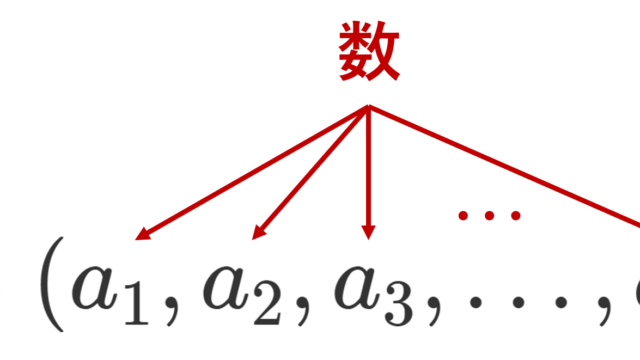 線形代数学
線形代数学 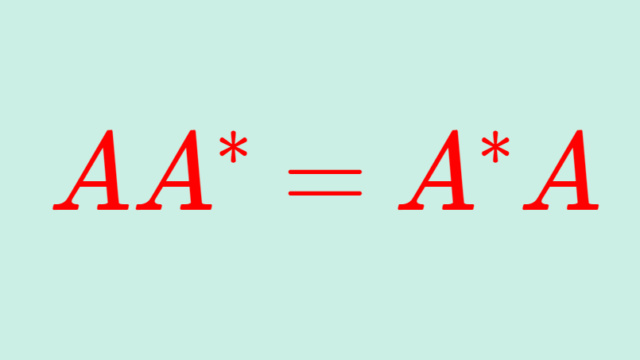 線形代数学
線形代数学 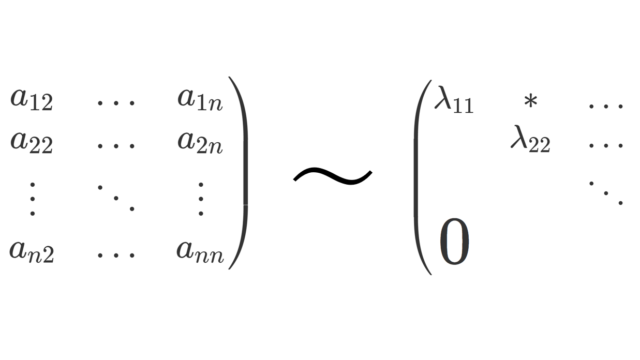 線形代数学
線形代数学  線形代数学
線形代数学