 線形代数学
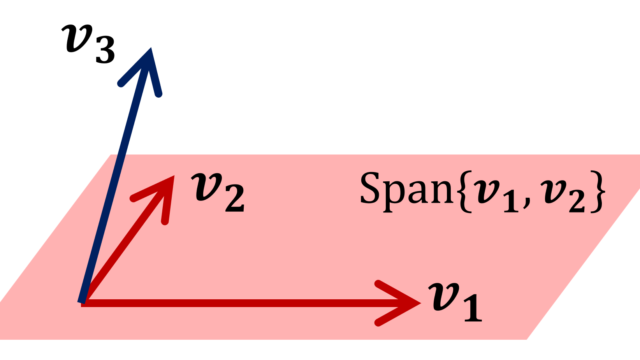
線形代数学 Spanの意味とは【線形結合】
Span Sとは集合Sの一次結合(線形結合)によってできるベクトル空間(線形包;linear span)を指します。これは,Sを含む最小のベクトル空間になります。Spanの定義と具体例を確認していきましょう。
 線形代数学
線形代数学  微分方程式
微分方程式 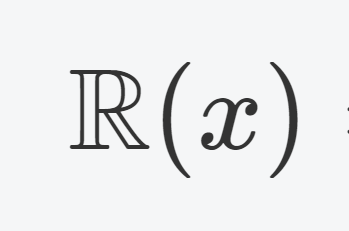 群・環・体
群・環・体  数論
数論 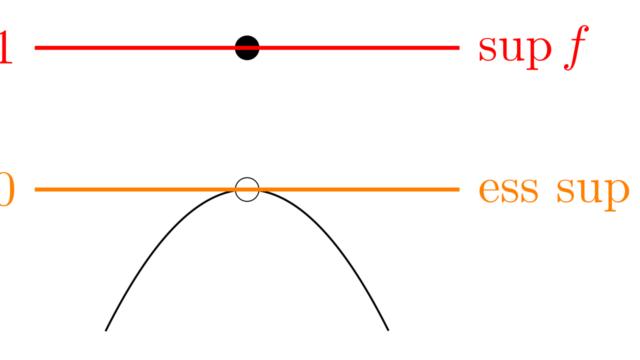 測度論
測度論 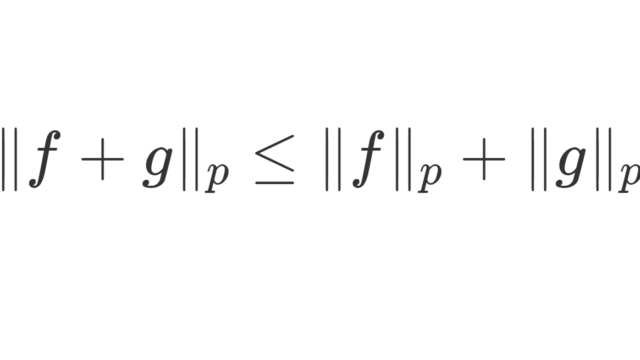 関数解析学
関数解析学 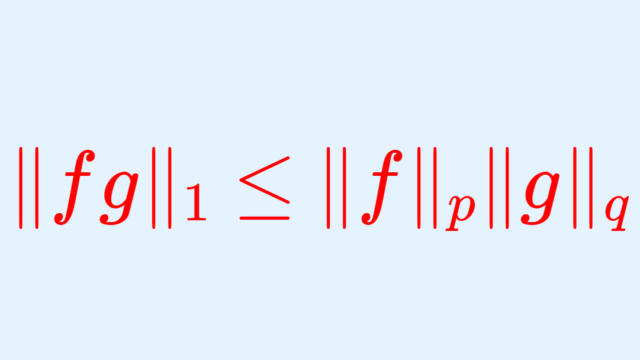 関数解析学
関数解析学 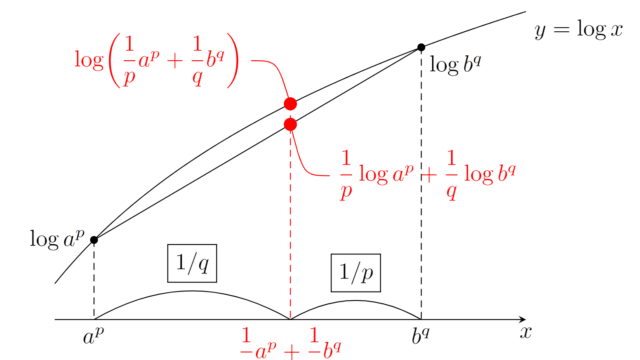 解析学(大学)その他
解析学(大学)その他 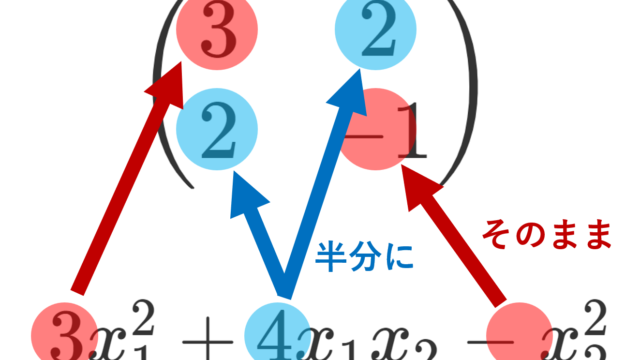 線形代数学
線形代数学 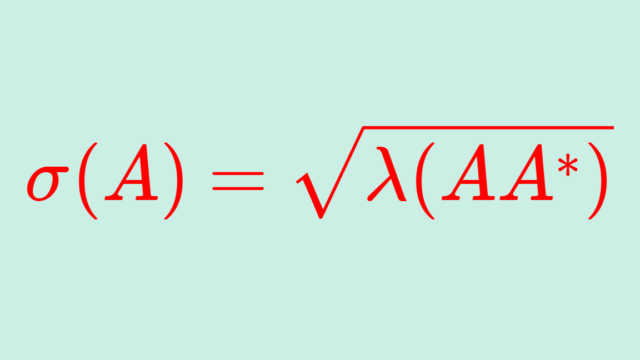 線形代数学
線形代数学