二次形式とは,2次の項しかない1変数または多変数多項式のことをいいます。二次形式について,その定義と,行列を用いた表し方を解説しましょう。
二次形式とは
定義(二次形式)
2次の斉次多項式,すなわち1次の項や定数項がない2次の多項式
\color{red}q(x_1,x_2,\dots, x_n)=\sum_{1\le i,j\le n}a_{ij} x_ix_j
を二次形式 (quadratic form) という。ただし, a_{ij}\in\R とする。
たとえば,1~3変数のときはそれぞれ
\begin{aligned}q(x)&=ax^2,\\ q(x,y)&= ax^2+bxy+cy^2,\\ q(x,y,z)&= ax^2+by^2+cz^2+dxy+eyz+fzx \end{aligned}
のような形です。
逆に,1次の項や定数項がある2次の多項式とは q(x)=ax^2+bx+c,\, q(x,y) = ax^2+bxy+cy^2+dx+ey+f のようなものです。 bx,c,dx,ey,f のように,1次や定数の項がありますね。こういうのは二次形式とは言いません。
なお,\sum_{ 1\le i,j\le n} とは, \{(i,j)\mid 1\le i,j\le n\} 全体にわたって和を取ることを意味し, \sum_{i=1}^n\sum_{j=1}^n でも同じ意味です。よって,厳密にはたとえば
\begin{aligned}q(x_1,x_2)&=\sum_{1\le i,j\le 2} a_{ij}x_iy_j\\ &= a_{11} x_1^2+a_{12}x_1x_2+a_{21} x_2x_1 +a_{22}x_2^2 \end{aligned}
ですが, x_1x_2=x_2x_1 ですから, a_{12}x_1x_2 と a_{21}x_2x_1 の項はまとめることができて,
ですね。よって, q(x,y)=ax^2+bxy+cy^2 とかけるわけです。3変数以上でも, x_ix_j と x_jx_i の項はまとめて (a_{ij}+a_{ji})x_ix_j とかけますね。
なお,ここで, a_{ij}, a_{ji} を a_{ij}+a_{ji} が一定のまま, a_{ij}=a_{ji} と取り直すことで(具体的には, a'_{ij}=a'_{ji}=\frac{a_{ij}+a_{ji}}{2} として, a'_{ij},a'_{ji} を新たな a_{ij},a_{ji} と思うことで), a_{ij}=a_{ji} としても良いです。
二次形式の行列表示
上で述べた, a_{ij}=a_{ji} としても良いことを用います。
定義(二次形式の行列表示)
\boldsymbol{x}=\begin{pmatrix} x_1 \\ \vdots \\ x_n\end{pmatrix} とする。このとき,A=(a_{ij}) とすると,
\color{red} q(x_1,\dots, x_n)=\sum_{1\le i,j\le n}a_{ij} x_ix_j=\boldsymbol{x}^\top A\boldsymbol{x}
とかける。とくに, a_{ij}=a_{ji} としてもよいので, A は実対称行列とできる。この実対称行列 A を二次形式の行列表示という。 \top は行列の転置の記号である。
二次形式の行列表示の作り方を考えていきましょう。二次形式を
q(x_1,\dots, x_n)=\sum_{i=1}^n a_{ii} x_i^2 + \sum_{1\le i<j\le n} 2a_{ij} x_ix_j
と表したときの対称行列 A=(a_{ij}) が行列表示ですから, x_i^2 の係数をそのまま対角成分とし, i\ne j のときは x_ix_j の係数を半分にして (i,j) 成分と (j,i) に当てはめればよいですね。
例題を見ておきましょう。
例題1.
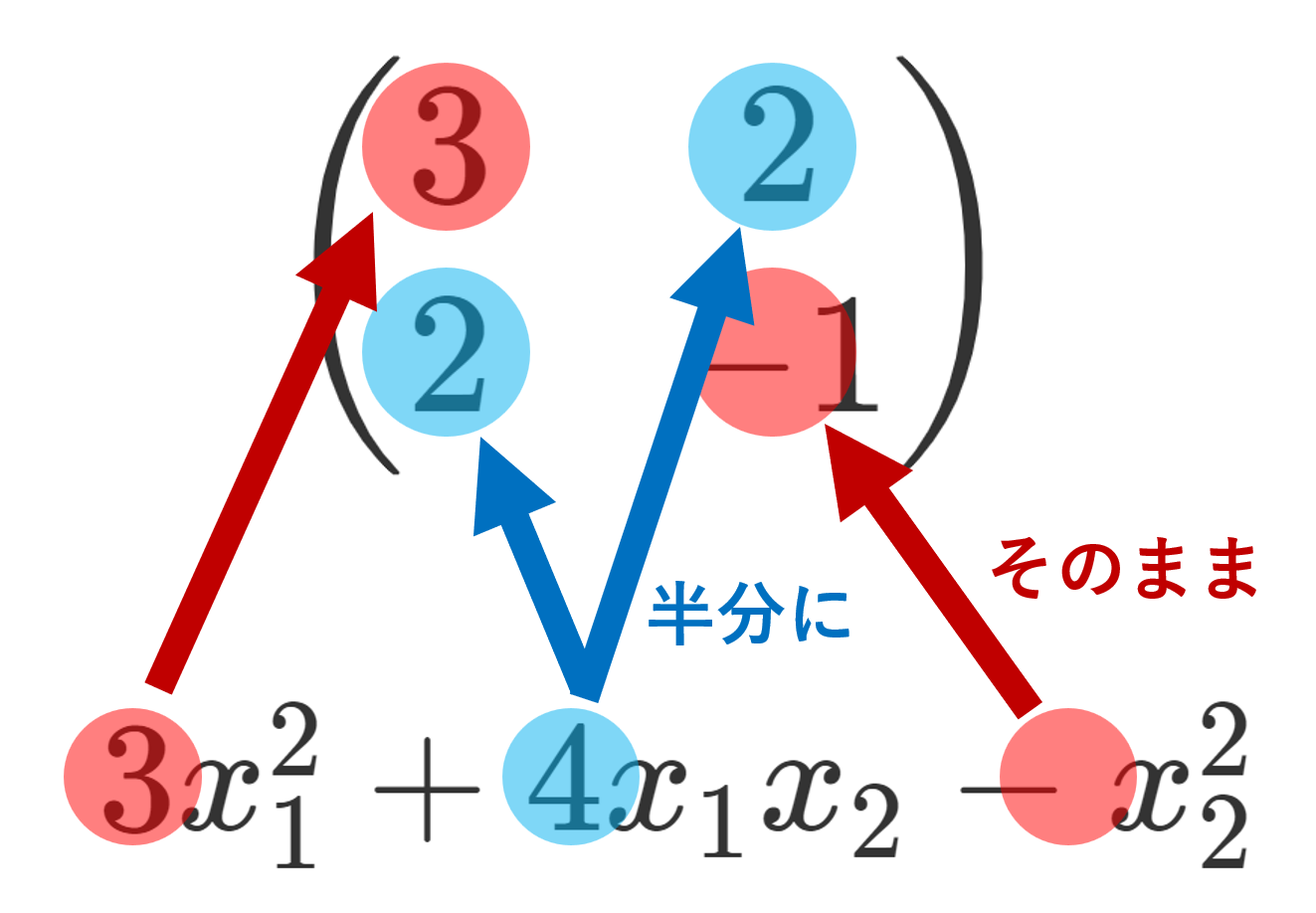
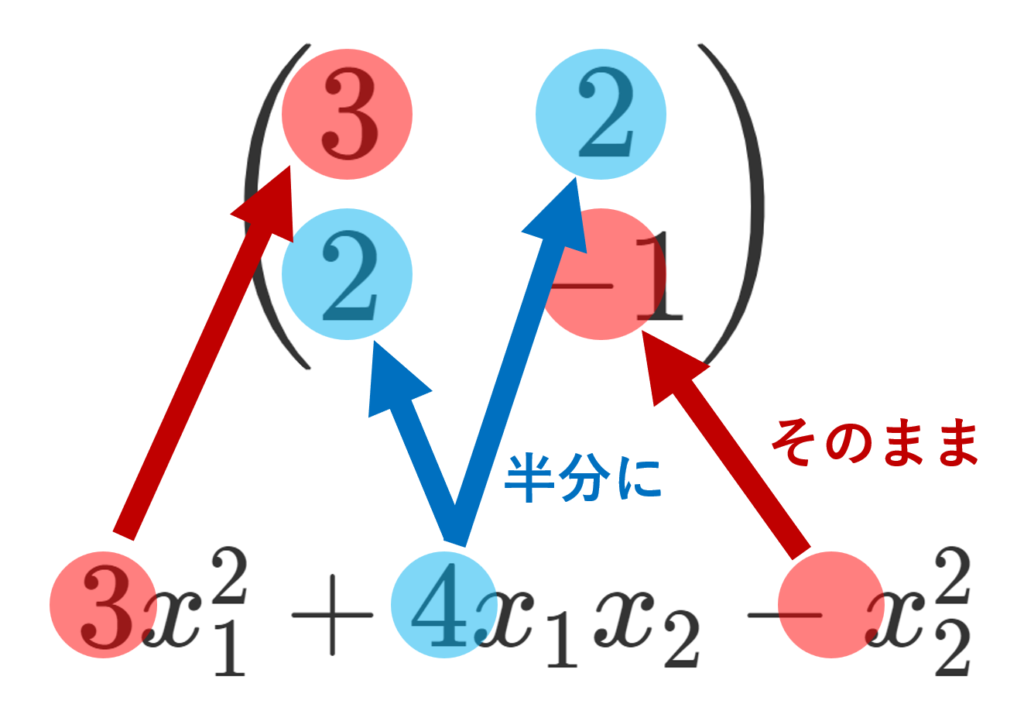
q(x_1,x_2)=3x_1^2+4x_1x_2-x_2^2 の行列表示を求めよ。
x_1^2, x_2^2 の係数はそのまま (1,1), (2,2) 成分に当てはめ, x_1x_2 の係数は半分にして (1,2),(2,1) 成分それぞれに当てはめるので,行列表示は
A=\begin{pmatrix} 3& 2\\ 2& -1 \end{pmatrix}
ですね。よって,
とかけるわけです。
例題2.
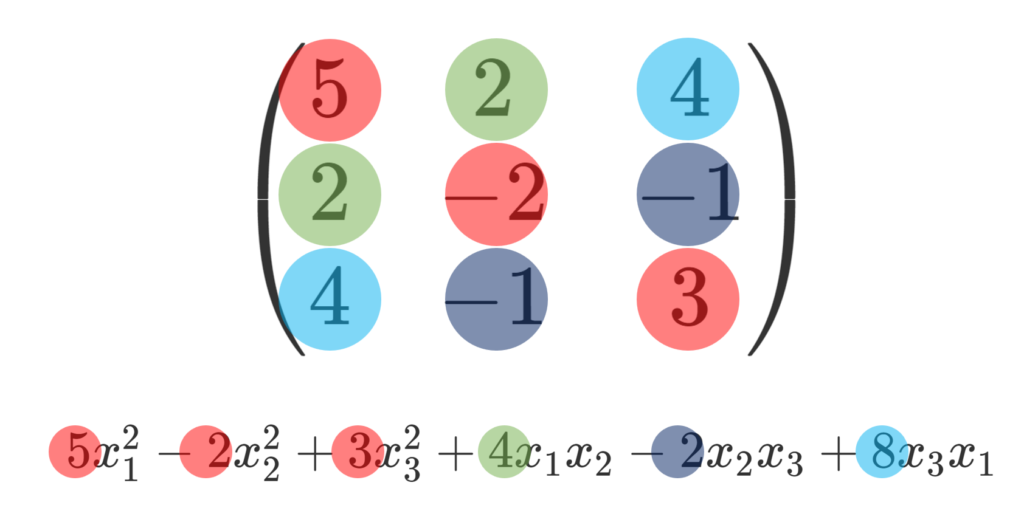
q(x_1,x_2,x_3)=5x_1^2-2x_2^2+3x_3^2+4x_1x_2-2x_2x_3+8x_3x_1 の行列表示を求めよ。
同様に考えると, 5x_1^2-2x_2^2+3x_3^2+4x_1x_2-2x_2x_3+8x_3x_1
A= \begin{pmatrix} 5& 2&4 \\ 2 & -2& -1 \\ 4 & -1& 3 \end{pmatrix}
ですね。よって,
とかけるわけです。
二次形式は数論や幾何学にも表れる,非常に重要な理論らしいですが,筆者はそうした方面への応用に詳しくありません。また勉強したら紹介します。