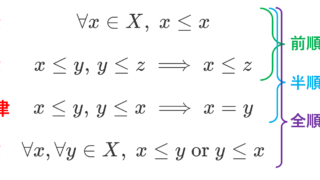集合において,同値関係の元を集めた「同値類」と,それらを集めた集合である「商集合」は,専門数学における難しい概念の1つでしょう。これについて,具体例・図を交えて解説します。
同値類と商集合の定義
定義(同値類・商集合)
X 上に同値関係 \sim が定まっているとする。このとき,
\color{red} [x]=\{ y\in X\mid x\sim y\}
を同値類 (equivalence class) という。また,同値類全体の集合を,集合 X の同値関係 \sim のよる商集合 (quotient set) といい,
とかく。
[x] は,代わりに \overline{x} や C(x) という記号を用いたりもします。
定義中に「同値関係」という言葉が出てきたので,一応復習しておきましょう。「同値関係」とは,以下の3つをみたす二項関係です。
詳しくは,以下で解説しています。
同値類は, x\sim y \iff [x]=[y] が成立し,逆に, x\not\sim y \iff [x]\cap [y] =\emptyset も成立します。
前半は明らかで,後半も,もし [x]\cap [y]\ne \emptyset ならば,共通部分の元の1つを z とすると, x\sim z\sim y となって, x\sim y ですから矛盾ですね。
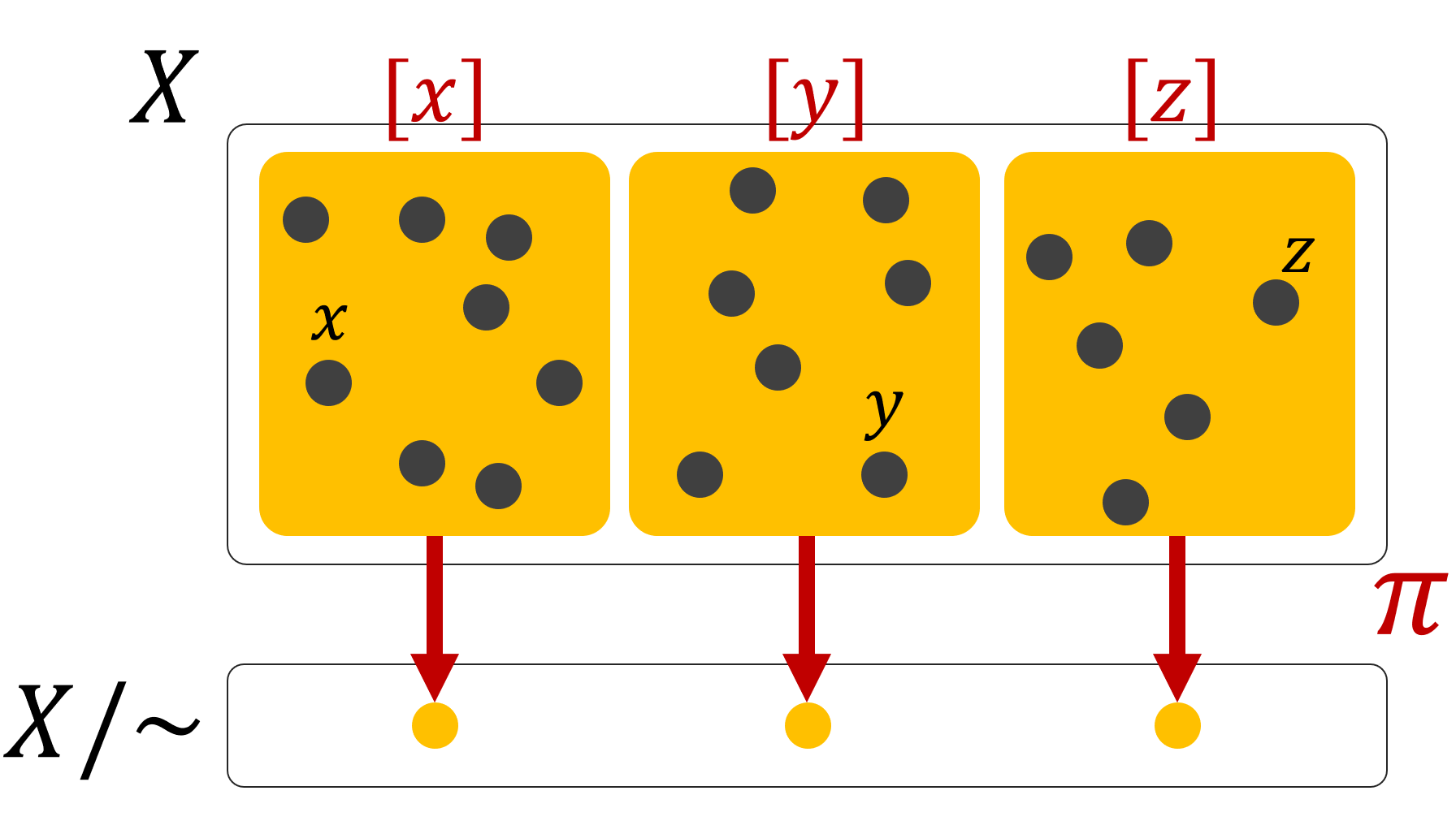
このことから,同値類によって,集合の元がいくつかの集合にグループ分けされることが分かるでしょう。
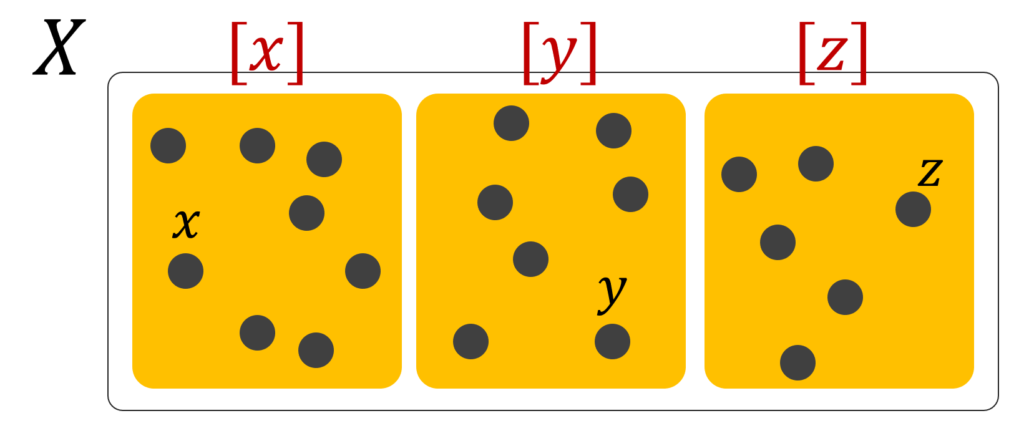
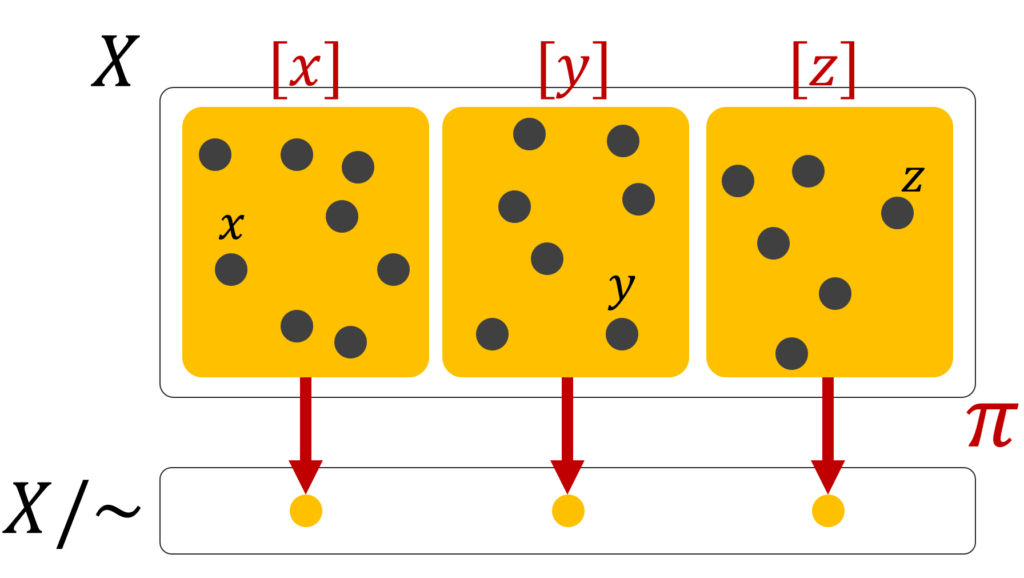
このグループ分けを一つの元と見て,それの集合を考えたのが,商集合なわけです。
このとき, x\mapsto [x] となる写像 \pi \colon X\to X/\!\sim が定まります。これを,自然な射影といいます。下図のように,この写像 \pi は射影的な見方ができますね。
同値類と商集合の具体例
理解には,やはり具体例を確認するのが一番でしょう。
例1.
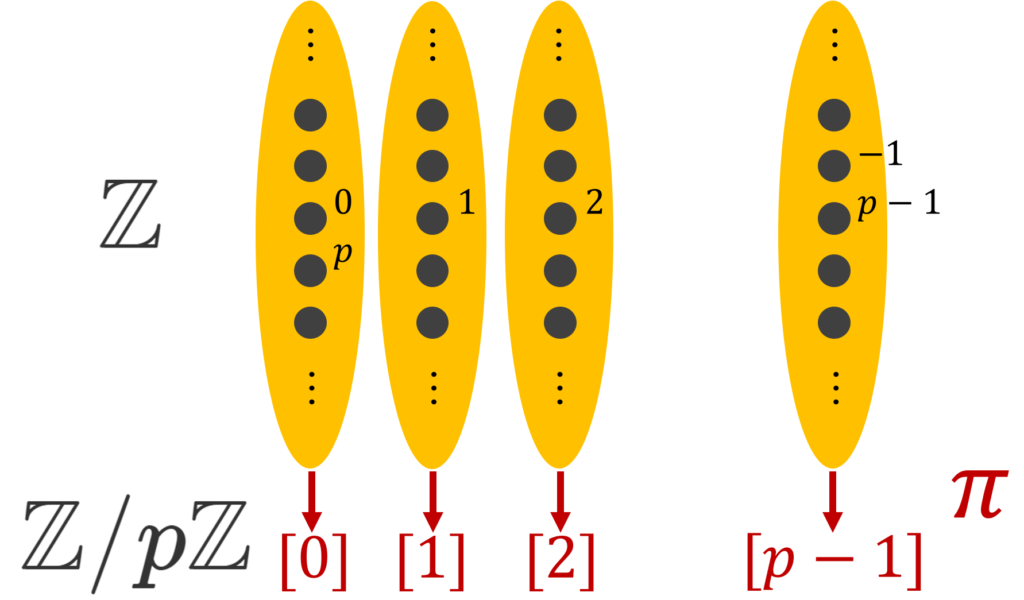
p を素数とする。整数全体の集合 \mathbb{Z} における, p を法とする合同関係 \equiv \pmod p は同値関係である。
この同値関係により,同値類 [0], [1],\dots, [p-1] を考えることができ,これを元とする,商集合 \mathbb{Z}/\!\! \equiv が作れる。
この同値類を剰余類 (residue class) という。この商集合を剰余体 (residue field) といい, \color{red} \mathbb{Z}/p\mathbb{Z} や \color{red} \mathbb{F}_p とかく。
\mod p の世界ですね。 p で割った余りについて,整数全体の集合 \mathbb{Z} 全体を分割し,同じ余りは同じものとみなしているわけです。
実際のところは,毎回 [0], [1], \dots, [p-1] のように括弧をつけるのは面倒なので,普通に 0,1,\dots, p-1 \in \mathbb{Z}/p\mathbb{Z} とかかれます。仰々しく n+p\mathbb{Z} \in \mathbb{Z}/p\mathbb{Z} とかくこともあります。
例2.
以下, S^1=\{ (x,y)\in\mathbb{R}^2\mid x^2+y^2=1\} を単位円とする。
f\colon \mathbb{R}\to S^1 を f(x)=(\cos x, \sin x) と定義し, x,y\in \mathbb{R} に対して,
x\sim y \stackrel{\mathrm{def}}{\iff} f(x)=f(y)
と定めた同値関係について,その商集合 \mathbb{R}/\!\!\equiv は \color{red}\mathbb{R}/2\pi\mathbb{Z} とかかれる。
\mod 2\pi の世界です。実際, x\sim y \iff x-y =2n\pi\; (n\in\mathbb{Z}) ですね。 2\pi の整数倍で等しいものを,同じものとみなします。イメージとしては,数直線を円周 2\pi の円に巻き付けて,重なるところを同一視する感じです。図で描くと,以下です。
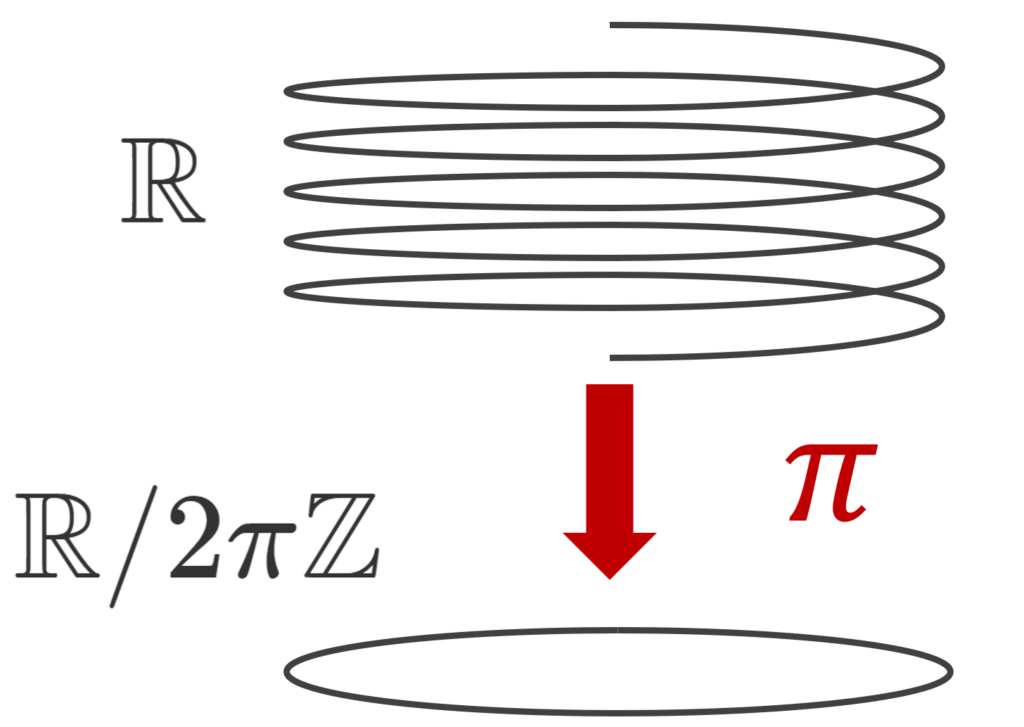
円周率の \pi と自然な射影の \pi\colon \mathbb{R}\to \mathbb{R}/2\pi\mathbb{Z} が文字被りしていますね。失礼いたしました。文脈で判断してください。
幾何学的には, \mathbb{R}/2\pi\mathbb{Z} は,1次元トーラスとも言われます。
さらに発展的な例を見ておきましょう。発展的といっても,数学科の学生にとってはごく身近なものです。
例3.
実数係数1変数多項式全体の集合 \mathbb{R}[X] を X^2+1 で割ったあまりで等しいものを合同と考える同値関係,すなわち,
f\equiv g \pmod{(X^2+1)} \stackrel{\mathrm{def}}{\iff} f-g は X^2+1 で割り切れる
について,その商集合 \mathbb{R}[X]/\!\!\equiv は \color{red} \mathbb{R}[X]/(X^2+1) とかかれる。
多項式の演算をそのまま引き継ぐ形で, \mathbb{R}[X]/(X^2+1) の上にも演算が定義でき(実際は和・差・積以外に商も定義でき),その演算は複素数 \mathbb{C} の演算と同じ(体として同型である)ことが知られています。
これは,実数の多項式の商集合を考えることで,複素数全体の集合が構成できるとも言えます。
次は,ベクトル空間の例です。
例4.
V,W をベクトル空間, f\colon V\to W を線形写像とする。 f の核(Ker)を \operatorname{Ker} f = \{ v\in V\mid f(v)=0\} とかくことにすると, v_1,v_2\in V について,
v_1 \sim v_2 \stackrel{\mathrm{def}}{\iff} v_1-v_2\in \operatorname{Ker} f
と定めた同値関係について,その商集合 V/\!\!\sim を \color{red} V/\operatorname{Ker} f とかく。
「準同型定理」でも使われる話ですね。この商集合もベクトル空間になっているため,商ベクトル空間とも言われます。