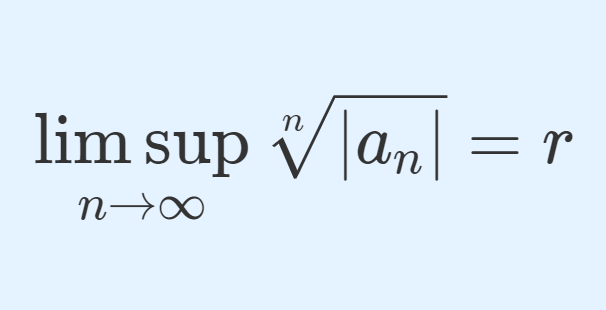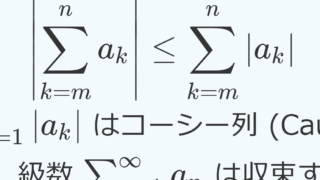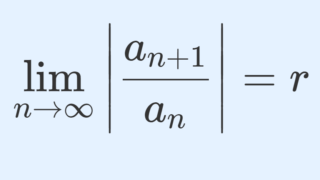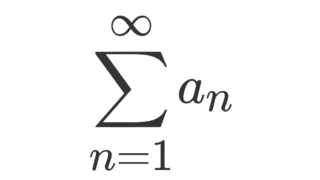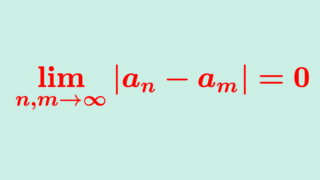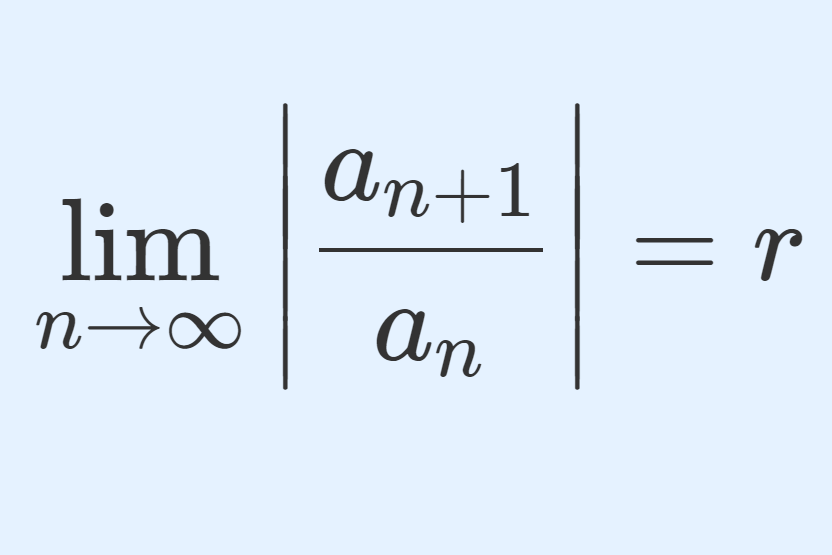級数 \sum_{n=1}^\infty a_n の収束・発散を判定する方法で有名なものの一つに,「コーシーの収束判定法」というものがあります。これの主張と具体例を紹介し,最後に証明を行います。
コーシーの収束判定法
定理(コーシーの収束判定法; Cauchy’s root test)
数列 \{a_n\} に対し,
\limsup_{n\to\infty} \sqrt[n]{|a_n|}= rとする。このとき, \sum_{n=1}^\infty a_n の収束・発散について
- 0 \le r < 1 ならば絶対収束
- r > 1 ならば発散
となる。
なお, r= 1 の場合は収束も発散もあり得ます。
これは,あくまで十分条件であることに注意してください。コーシーの判定法が使えないが収束・発散する例については後で述べます。
また,絶対収束すなわち \sum_{n=1}^\infty |a_n| < \infty となるとき,元の級数 \sum_{n=1}^\infty a_n も有限値に収束することは有名です。これについての証明は以下を参照してください。
コーシーの収束判定法の具体例
まずは,さまざまな具体例を挙げることにしましょう。
コーシーの判定法が適用できる例
絶対収束する例
例1.
\textcolor{red}{a_n = (1/\log \log (n+1))^{n}} とする。このとき,
\begin{aligned} \lim_{n\to\infty}\sqrt[n]{\left( \frac{1}{\log\log (n+1) }\right)^n } &= \lim_{n\to\infty} \frac{1}{\log \log (n+1) } \\ &= 0 \end{aligned}より,コーシーの判定法が使えて,
\textcolor{red}{\sum_{n=1}^\infty \left(\frac{1}{\log\log (n+1)}\right)^n < \infty.}すなわち,絶対収束となる。
例2.
\textcolor{red}{a_n = (x+1/n)^{n}, \,\, 0\le x< 1} とする。このとき,
\begin{aligned} \lim_{n\to\infty}\sqrt[n]{\left(x+\frac{1}{n}\right)^{n} } &= \lim_{n\to\infty} \left(x+\frac{1}{n}\right) \\ &= x < 1 \end{aligned}より,コーシーの判定法が使えて,
\textcolor{red}{\sum_{n=1}^\infty \left(x+\frac{1}{n}\right)^{n} < \infty.}すなわち,絶対収束となる。
例3.
\textcolor{red}{a_n = (1-1/n)^{n^2}} とする。このとき,
\begin{aligned} \lim_{n\to\infty}\sqrt[n]{\left(1-\frac{1}{n}\right)^{n^2} } &= \lim_{n\to\infty} \left(1-\frac{1}{n}\right)^{n} \\ &= \frac{1}{e} < 1 \end{aligned}より,コーシーの判定法が使えて,
\textcolor{red}{\sum_{n=1}^\infty \left(1-\frac{1}{n}\right)^{n^2} < \infty.}すなわち,絶対収束となる。
ここで, a^{b^c} とは, a^{(b^c)} の意味になります。
発散する例
例4.
\textcolor{red}{a_n=2^{(-1)^n n}} とする。このとき,
\begin{aligned} \limsup_{n\to\infty}\sqrt[n]{ 2^{(-1)^n n}} &= \limsup_{n\to\infty} 2^{(-1)^n} \\ &= 2 > 1 \end{aligned}より,コーシーの判定法が使えて,
\textcolor{red}{\sum_{n=1}^\infty 2^{(-1)^n n} = \infty.}すなわち,発散する。
r = 1 となる例
コーシーの判定法が適用できない例とは,すなわち r = 1 となる例なので,そのような例を見ていきましょう。
絶対収束する例
例5.
\textcolor{red}{a_n = 1/n^2} とする。このとき,
\begin{aligned} \lim_{n\to\infty} \sqrt[n]{\frac{1}{n^2}} = 1 \end{aligned}より,コーシーの判定法は使えないが,
\textcolor{red}{\sum_{n=1}^\infty \frac{1}{n^2} < \infty. }すなわち,絶対収束する。
条件収束する例
例6.
\textcolor{red}{a_n = (-1)^n/n} とする。このとき,
\begin{aligned} \lim_{n\to\infty}\sqrt[n]{\left|\frac{(-1)^n}{ n}\right| } = 1 \end{aligned}より,コーシーの判定法が使えないが,
\textcolor{red}{\sum_{n=1}^\infty \frac{1}{n} = \infty, \quad \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} = \log 2.}すなわち,条件収束する。
発散する例
例7.
\textcolor{red}{a_n = (1-1/n)^{n}} とする。このとき,
\begin{aligned} \lim_{n\to\infty}\sqrt[n]{\left(1-\frac{1}{n}\right)^{n} } &= \lim_{n\to\infty} \left(1-\frac{1}{n}\right)\\ &= 1 \end{aligned}より,コーシーの判定法は使えないが, \lim_{n\to\infty} (1-1/n)^{n} = 1/e \ne 0 より, \{a_n\} は 0 に収束せず正のため,
\textcolor{red}{\sum_{n=1}^\infty \left(1-\frac{1}{n}\right)^{n} = \infty.}すなわち,発散する。
例8.
\textcolor{red}{a_n = (-1)^n} とする。このとき,
\begin{aligned} \lim_{n\to\infty}\sqrt[n]{|(-1)^n| } = 1 \end{aligned}より,コーシーの判定法は使えないが,明らかに \sum_{n=1}^\infty (-1)^n は収束しない。
さまざまな具体例を確認できました。
コーシーの収束判定法の証明
さて,証明を行いましょう。 0 \le r < 1, r > 1 を別々に行います。
絶対収束する証明
証明; 0 \le r < 1 のとき
\varepsilon > 0 を r + \varepsilon < 1 となるように取る。\limsup_{n\to\infty} \sqrt[n]{|a_n|} = r より,ある N \ge 1 が存在して,
n\ge N \implies \sqrt[n]{|a_n|} \le r + \varepsilonとできる。すなわち,
n\ge N \implies |a_n| \le (r + \varepsilon)^nである。これにより,
\begin{aligned} &\sum_{k=1}^{N+n}| a_k| \\ &= \sum_{k=1}^{N-1} |a_k| + \sum_{k=0}^n |a_{N+k}| \\ &\le \sum_{k=1}^{N-1} |a_k| + \sum_{k=0}^n (r+\varepsilon)^{N+k} \\ &\le \sum_{k=1}^{N-1} |a_k| + \sum_{k=0}^\infty (r+\varepsilon)^k \\ &= \sum_{k=1}^{N-1} |a_k| + \frac{1}{1-r-\varepsilon} \end{aligned}であり,右辺は n によらないから,左辺で n\to\infty として, \sum_{k=1}^\infty |a_k| < \infty, すなわち絶対収束を得る。
証明終
発散する証明
証明; r > 1 のとき
\varepsilon > 0 を r - \varepsilon > 1 となるように取る。\limsup_{n\to\infty} \sqrt[n]{|a_n|} = r より,ある部分列 \{a_{n_k}\} が存在して,
\lim_{k\to\infty} \sqrt[n]{|a_{n_k}|} = rとなる。これより,さらに N \ge 1 が存在して,
k\ge N \implies \sqrt[n]{|a_{n_k}|} \ge r - \varepsilonとできる。すなわち,
k\ge N \implies |a_{n_k}| \ge (r - \varepsilon)^kであり,右側の両辺 \liminf_{k\to\infty} をとることで,
\lim_{k\to\infty} |a_{n_k}| = \inftyがわかる。特に \lim_{n\to\infty} a_n = 0 とならなくなってしまうため,元の級数は収束しない。
証明終
その他の収束判定法
コーシーの収束判定法以外にも,ダランベールの収束判定法は有名です。これについては,以下の記事を参照してください。
また,ダランベールの収束判定法はコーシーの収束判定法より使いやすい反面,コーシーの収束判定法の方が適用範囲が広いことが知られています。これについては以下の記事を参照してください。
また,他にも以下でさまざまな判定法をまとめています
あいまい検索
コーシー列 (Cauchy sequence) とは概念が異なります。これについては以下の記事を参照してください。