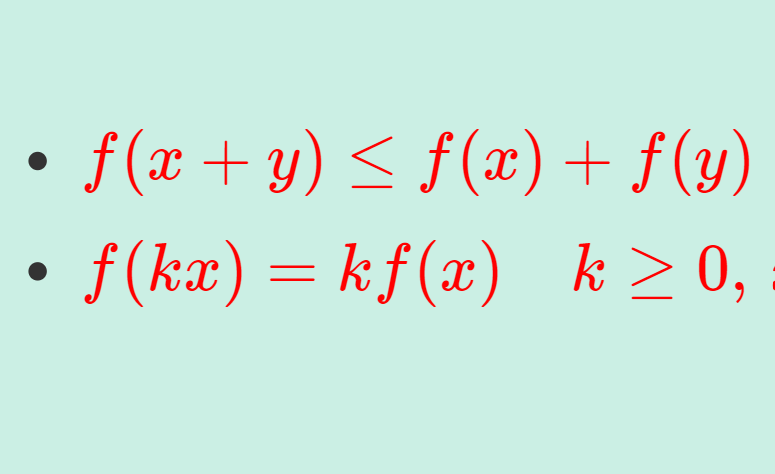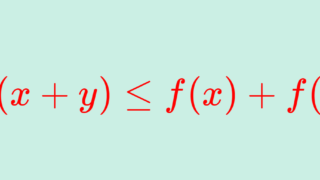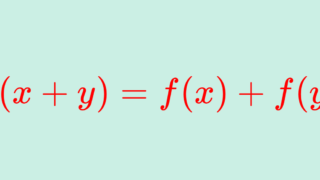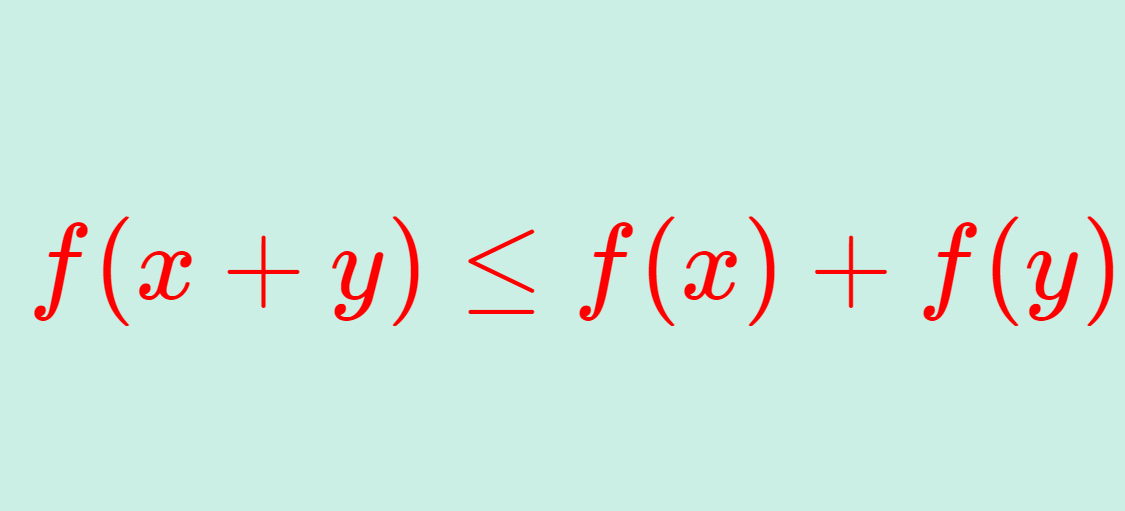劣線形的関数 (sublinear function) の定義と具体例・性質をまとめます。
劣線形的関数の定義
定義(劣線形的関数)
X を \mathbb{R} または \mathbb{C} 上ベクトル空間とする。
f\colon X \to \mathbb{R} が劣線形的 (sublinear; positive-homogeneous subadditive function) とは以下の2つが成立することである。
- \textcolor{red}{f(x+y) \le f(x) + f(y) \quad x,y \in X,}
- \textcolor{red}{f(kx) = kf(x) \quad k \ge 0,\, x\in X.}
定義域はベクトル空間としましたが,単に \mathbb{R}^n, \mathbb{C}^n でもよいです(これもベクトル空間です)。
なお,2項目のうち,1つ目のみ成立する関数を劣加法的関数 (subadditive function) といいます。これの性質ついては,以下で解説しています。
ここでは,以上で述べている性質は挙げませんので,適宜参照してください。
劣線形的関数の具体例
具体例を2つ挙げておきましょう。
劣線形的関数の具体例
- f\colon \mathbb{R} \to \mathbb{R}, \, a \in \mathbb{R} に対し,
\textcolor{red}{ f(x) = ax} は劣線形的である。 - X をノルム空間とする。 f\colon X \to \mathbb{R} に対し,
\textcolor{red}{f(x) = \| x \| } は劣線形的である。
劣線形的関数の性質
2.の性質より,劣線形的関数は,凸関数の性質も成立することが分かります。
証明
1. f(0) = 2 f(0) より。
2. x,y \in \mathbb{R}^n に対し,
\begin{aligned} f\left(\frac{x+y}{2}\right) &= \frac{1}{2} f(x+y) \\ &\le \frac{f(x)+f(y)}{2} \end{aligned}
であるから,凸である。
証明終
証明しませんが,他に1次元かつ可測の場合は単純にかけます。
定理 (See, e.g., [2, Theorem 16.4.3.])
f\colon \mathbb{R} \to \mathbb{R} が可測な劣線形的関数とすると,ある a \ge b が存在して,
f(x) = \begin{cases} ax & x \ge 0, \\ bx & x < 0 \end{cases}
とかける。
他の性質は下に挙げた参考文献等を見てください。
関連する記事
参考文献
- E. Hille, R. S. Phillips, Functional analysis and semi-groups, American Mathematical Society, 1957.
- M. Kuczma, An introduction to the theory of functional equations and inequalities, 2nd edition. Birkhäuser Verlag, 2009.