数列(あるいは関数列・点列など)における「部分列」とは何か解説し,部分列に関連するテーマを紹介します。
部分列の定義と具体例
部分列の定義と具体例を述べましょう。
部分列の定義
定義(部分列)
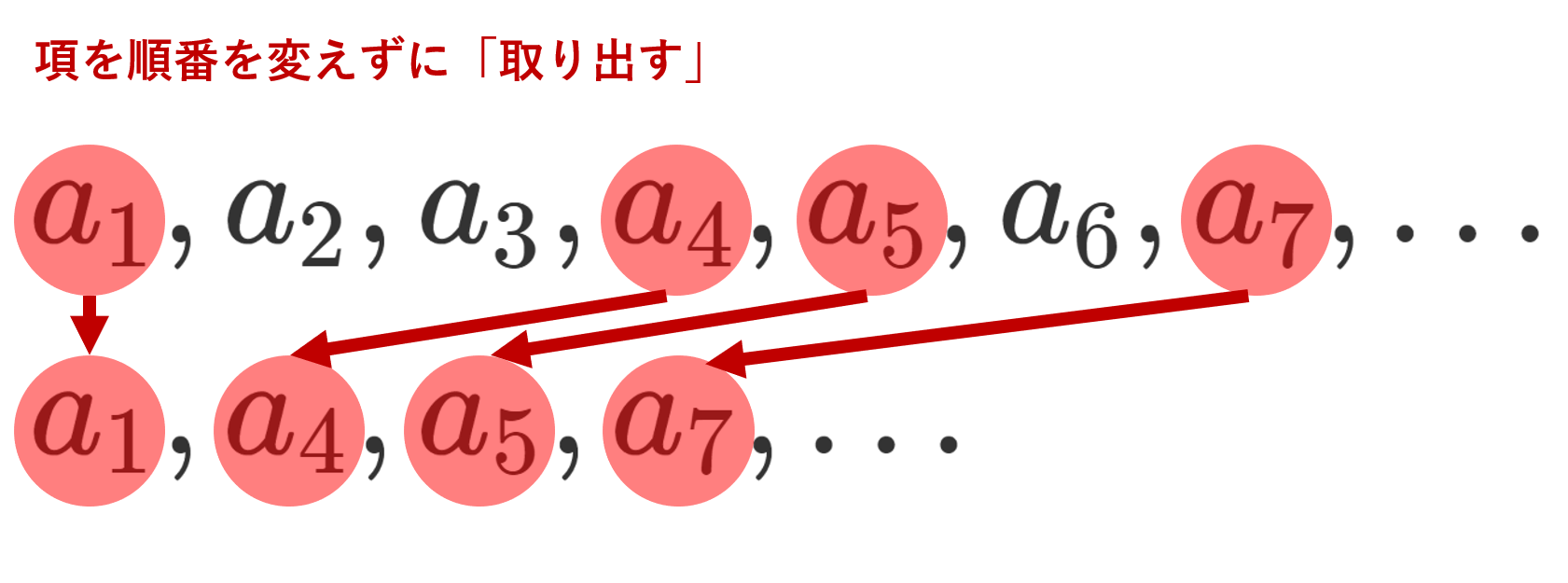
\{a_n\} を数列とする。このとき,項の一部を(無限個)取り出し,順番を変えずに並べた数列を部分列 (subsequence) という。
今は数列としましたが,どんな列でも部分列を考えることができます。
イメージとしては,以下のような感じです。あくまで一例で他の取り出し方もあります。
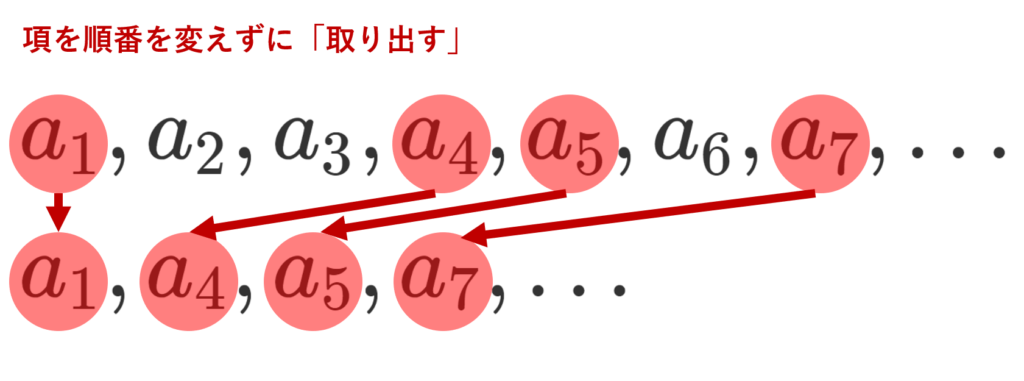
部分列は添え字を n \,\,(n=1,2,3,\dots) から n_k\,\, (k=1,2,3,\dots) に変えて \color{red} \{a_{n_k}\} などと書かれたりします。
部分列は,集合として \{a_{n_k}\} \subset \{a_n\} が成立します。
部分列の具体例
具体例を3つ挙げましょう。
部分列の具体例
- \color{red} \{a_{2n}\} は \{a_n\} の偶数項のみを取り出した部分列である。
- \color{red}\{a_{n^2}\} は \{a_n\} の第 n^2 項を取り出した部分列である。
- a_2, a_1, a_4, \dots は項の順番が変わっているので部分列でない。
写像の言葉を用いた,より厳密な部分列の定義
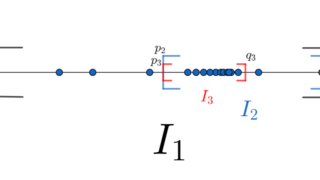
上の部分列の定義が理解できれば十分なのですが,一応写像を用いて,より感覚的な部分を排除した定義を紹介します。
定義(部分列の厳密な定義)
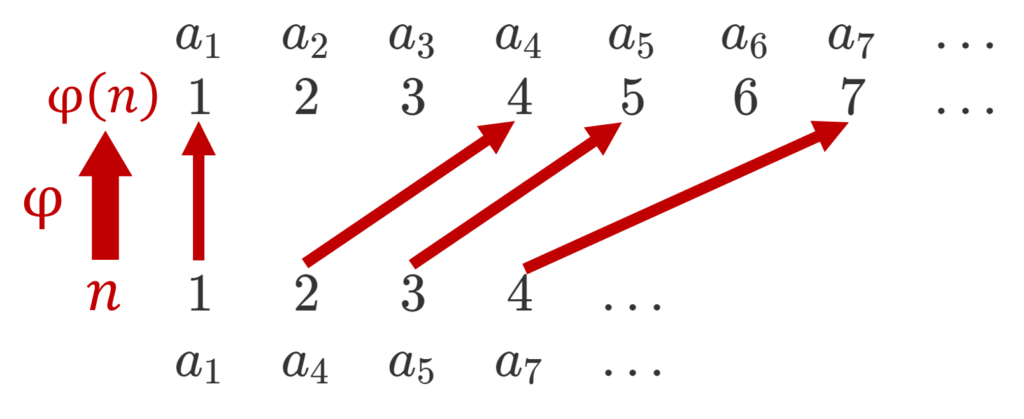
\{a_n\} を数列とし, \varphi\colon \mathbb{N} \to\mathbb{N} を順序を保つ単射であるとする。
すなわち,
\color{red}n < m \implies \varphi(n) < \varphi(m)
とする。このとき, \{a_{\varphi(n)}\} を部分列 (subsequence) という。
ただし, \mathbb{N} = \{1,2,3,\dots\} は正の整数全体の集合とする。
「単射」とは「1対1の写像・関数」であるということです。この定義について具体的には,全射・単射・全単射の定義をわかりやすく~具体例を添えて~を参照してください。
ちょっと分かりにくいかもしれませんが,イメージ図としては以下のような感じです。
部分列に関係する話
ここからは,部分列に関係する話を紹介します。
ボルツァノ-ワイエルシュトラスの定理
定理(ボルツァノ–ワイエルシュトラス;Bolzano–Weierstrass)
数列 \{a_n\} \subset \mathbb{R} が有界のとき,これは収束部分列を持つ。
実数の数列が有界であれば,収束部分列を必ず持つと言っています。この定理をボルツァノ-ワイエルシュトラスの定理といい,解析学の基本的な定理の1つです。
これの証明については,以下の記事で解説しています。
アスコリ-アルツェラの定理
定理(アスコリ–アルツェラ; Ascoli–Arzelà)
関数列 \{f_n\} は定義域が区間 [a,b] である連続関数の列とする( -\infty < a < b < \infty )。この関数列が一様有界かつ同程度連続であるならば,一様収束する部分列が存在する。
アスコリ-アルツェラの定理は,関数列の部分列に着目した定理です。
これについては,以下の記事で解説しています。
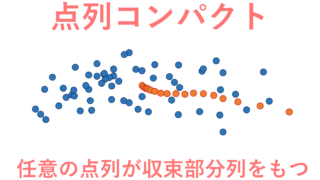
点列コンパクト
点列コンパクトの話は,かなり高度な数学を必要としますが,定義を理解するだけであれば可能でしょう。ただし,「位相空間」という言葉は「なんかそういう集合がある」とでも思ってください。
定義(点列コンパクト)
X を位相空間とする。 X が点列コンパクト (sequentially compact) であるとは, X 上の任意の点列が X 内に収束する部分列を持つことを言う。
実数上の任意の有界閉集合は点列コンパクトであることが,上のボルツァノ-ワイエルシュトラスの定理からわかります。点列コンパクト性については,以下で解説しています。