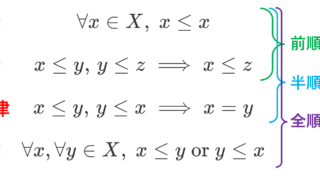上限(sup)・下限(inf)の定義を述べ,それが最小上界・最大下界になることの証明と,最大値(max)・最小値(min)との違いを考えます。
上限,下限(sup,inf)の定義
まずは実数の部分集合における上限・下限を定義を紹介し,さらにそれと同値な定義(最小上界・最大下界になることの証明)も紹介します。
上限,下限(sup,inf)の定義
定義(上限・下限)
A \subset \mathbb{R} を空でないとする。
\alpha \in \mathbb{R} が A の上限 (supremum) であるとは,
- x \in A \implies x \le \alpha,
- 任意の \varepsilon > 0 に対し,ある x \in A が存在して, \alpha - \varepsilon \le x \le \alpha
の両方が成立することを指す。このとき, \color{red} \sup A = \alpha とかく。
A が上に有界でないときは \color{red} \sup A = \infty と定義し,逆に多くの場合,慣習により \color{red} \sup \varnothing = - \infty と定める。
\beta \in \mathbb{R} が A の下限 (infimum) であるとは,
- x \in A \implies \beta \le x,
- 任意の \varepsilon > 0 に対し,ある x \in A が存在して, \beta \le x \le \beta + \varepsilon
の両方が成立することを指す。このとき, \color{red} \inf A = \beta とかく。
A が下に有界でないときは \color{red} \inf A = -\infty と定義し,逆に多くの場合,慣習により \color{red} \inf \varnothing = \infty と定める。
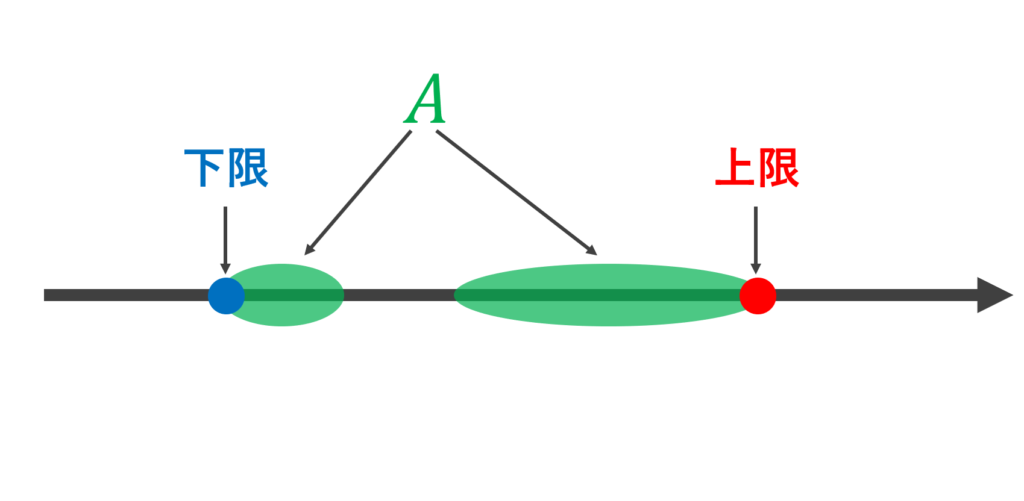
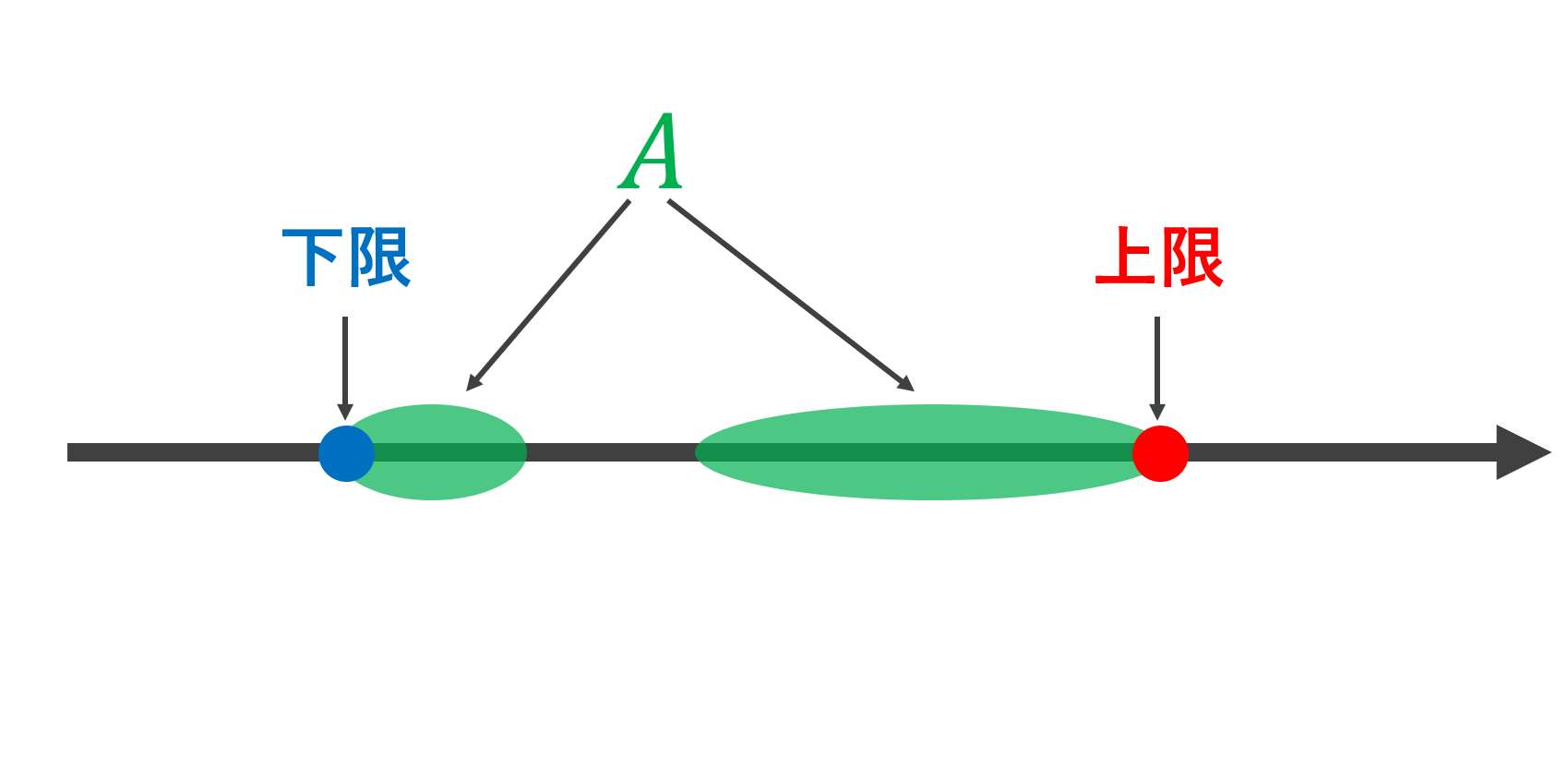
1.の式 x \in A \implies x \le \alpha, \,\, x \in A \implies \beta \le x は,\alpha, \beta がそれぞれ上界・下界になると言っています。さらに,2.の式より, \alpha, \beta はそれぞれ最小上界・最大下界,すなわち上界全体の集合の最小値・下界全体の集合の最大値になっていることが分かります。
よってこれを定義にしてもよいです。詳しく述べましょう。
上界,下界を用いた上限,下限(sup,inf)の同値な定義
なお,実数の部分集合でない一般の半順序集合 (X, \le) における上限・下限は,これを定義とします。もちろん,実数のときもこれを定義として差し支えないです。
上限・下限の証明は同様なので,上限の方のみ証明しましょう。
証明
上限 \implies 最小上界について
上限を \alpha = \sup A とする。上限の定義1.の x \in A \implies x \le \alpha により, \alpha は上界である。
\alpha が最小上界でないとすると, \alpha' < \alpha となる上界 \alpha' が存在するが,これは定義2.に反する。
最小上界 \implies 上限について
上界全体の集合の最小値はただ一つであることと,(次項で解説している通り)上限が必ず存在することにより,これが成り立たねばならない。
なぜならば,最小上界であって上限でないものがあるとすると,別に上限がある。しかしこの上限は前半の証明から,最小上界である。最小上界は一つしかないから,これはおかしい。
証明終
実数の部分集合における上限・下限は必ず存在する
次は実数の連続性にまつわる公理です。
公理( \sup,\inf の存在)
- 実数の上に有界な部分集合は必ず(有限な)上限を持つ
- 実数の下に有界な部分集合は必ず(有限な)下限を持つ
今回は公理としましたが,実数の四則演算・大小関係とデデキント切断 (Dedekind cut) による実数の構成を採用すると,これは定理として証明できます。詳しくは,以下で解説しています。
上限,下限(sup,inf)と最大,最小(max,min)との違い
ここで, \sup \{ f(x) \mid x \in A \} は \sup_{x\in A } f(x) とも書かれることに注意しましょう。このことを踏まえて両者の違い,特にここでは \sup と \max の違いをを確認していきます。
まずは両者の定義を述べましょう。
\alpha = \sup A であるとは,
任意の \varepsilon > 0 に対し,ある x \in A が存在して, \alpha - \varepsilon \le x \le \alpha かつ任意の x \in A に対して x \le \alpha
が成立することである。
\alpha = \max A であるとは,
\alpha \in A かつ任意の x \in A に対して x \le \alpha
が成立することである。
\max と \sup の最も大きな違いは, \alpha \in A か否かです。最大値は \alpha \in A でなければなりませんが, \sup はその必要はありません。
これが影響して, \sup は必ず存在しますが, \max は存在しなくても構いません。
具体例を挙げましょう。
上限(sup)と最大(max)の違いの具体例
| 関数 | 図 | 最大値 | 上限 |
|---|---|---|---|
| f(x) = -x^2 \\(x\in \mathbb{R}) | 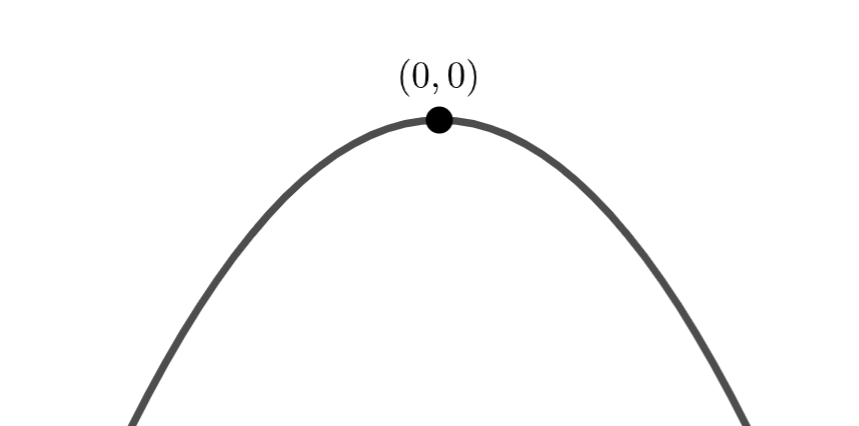 | 0 | 0 |
| f(x) = x^2 \\ (-1 \le x\le 1) |  | 1 | 1 |
| f(x) = x^2\\(-1 < x < 1) |  | なし | 1 |
| f(x) = x^2 \\(x\in \mathbb{R}) | 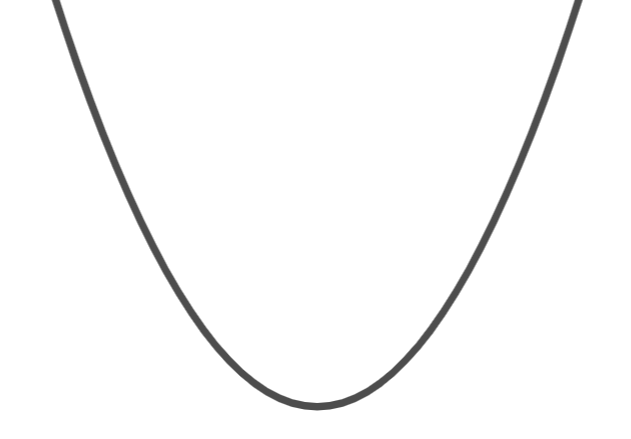 | なし | \infty |
| f(x) = -1/x \\(x>0) | 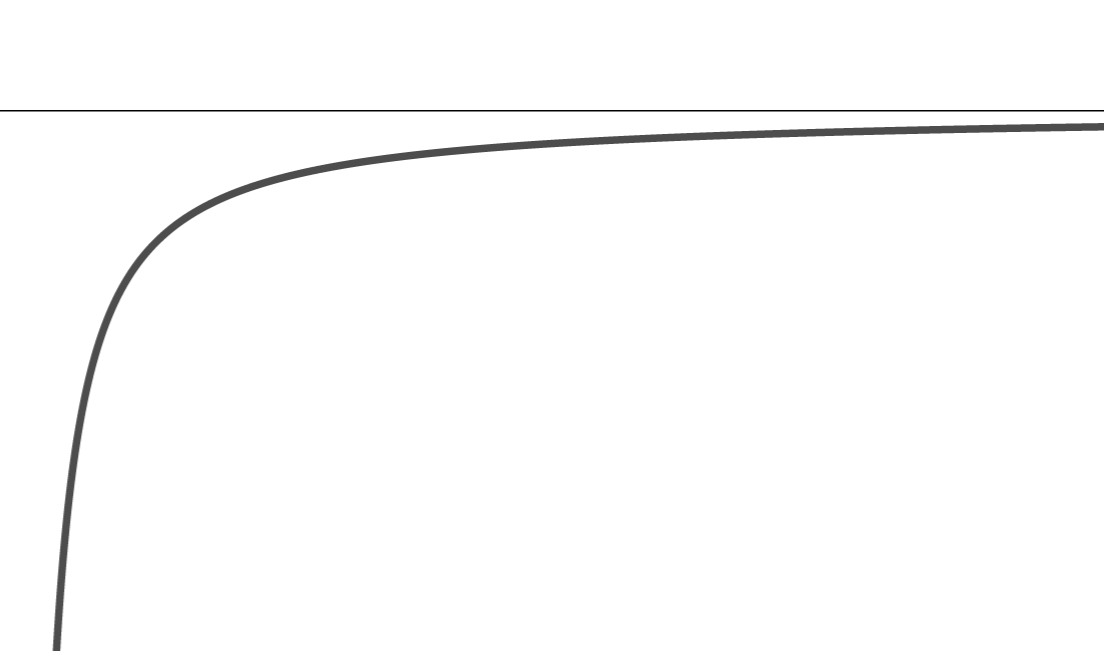 | なし | 0 |
定義にも記しましたが,集合が上に有界でない場合(4つ目の場合),上限は \infty と考えることに注意してください。
下限(inf)と最小値(min)の違いも同様です。なんとなく違いが分かれば幸いです。
最大値・最小値が存在するとき上限・下限はそれに一致する
上の例において,最大値があるときは,上限も同じ値になっていることが分かるでしょう。この点で「上限は最大値の拡張概念」と思うこともできます。実際,以下が成立します。
定理
A \subset \mathbb{R} に対し, \max A が存在するとき, \color{red} \sup A = \max A である。同様に \min A が存在するとき, \color{red} \inf A = \min A である。
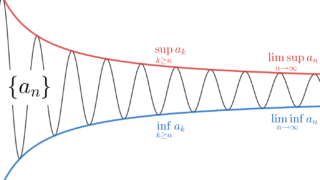
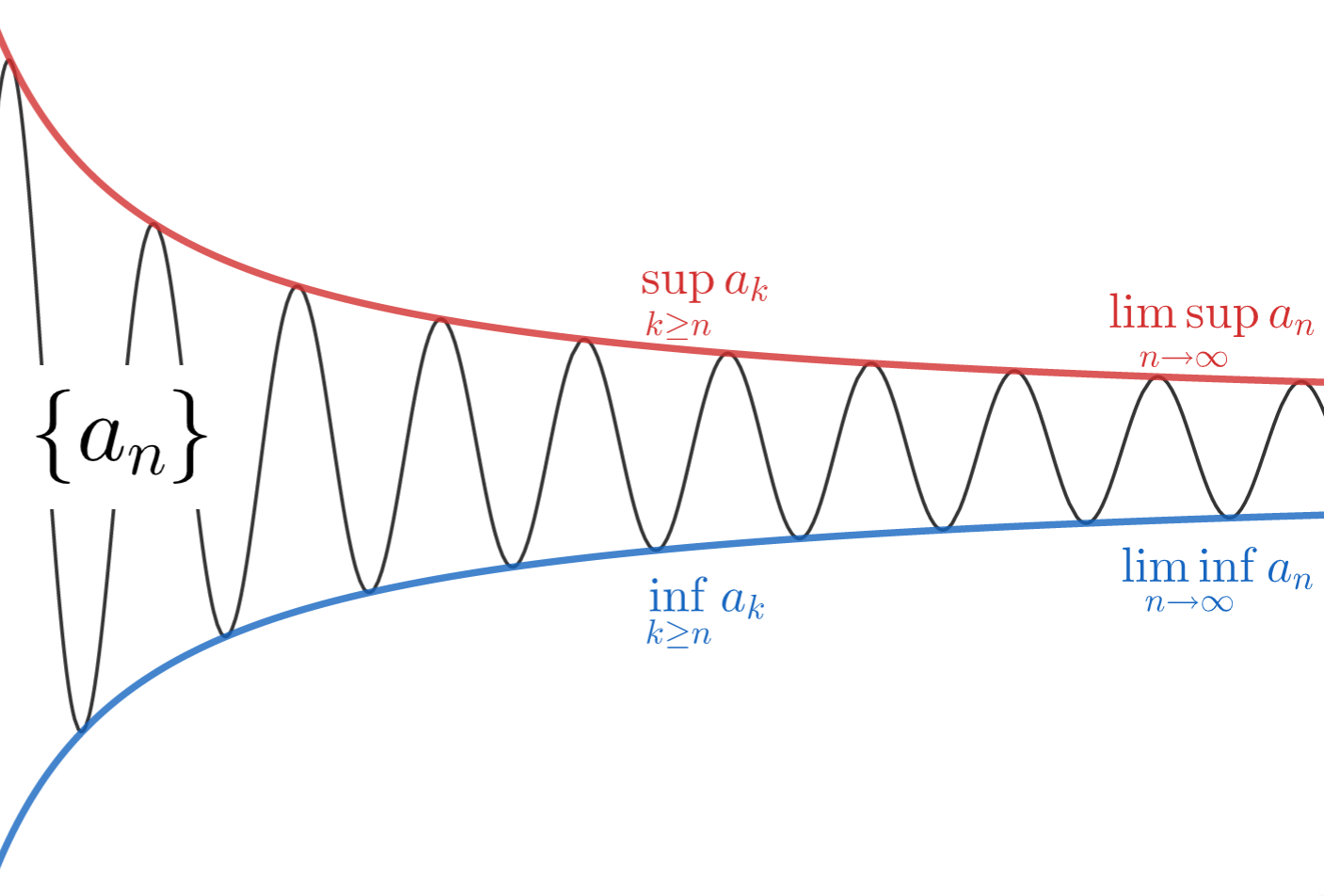
上極限・下極限(limsup,liminf)
上限・下限と極限を組み合わせたもので,上極限・下極限というものがあります。これについては,以下で解説しています。
より一般の順序集合における上限・下限
以下を参照してください。