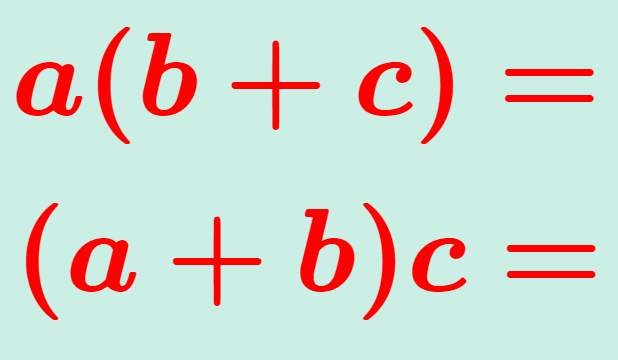 群・環・体
群・環・体 環の定義・可換環の定義とその具体例6つ
代数学における,環 (ring) ・可換環 (commutative ring) とは,足し算と掛け算を考えられる集合を指します。環の定義・可換環の定義について述べ,その具体例も挙げていきましょう。
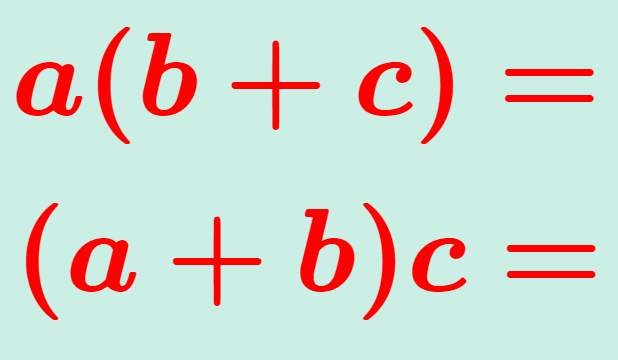 群・環・体
群・環・体  線形代数学
線形代数学 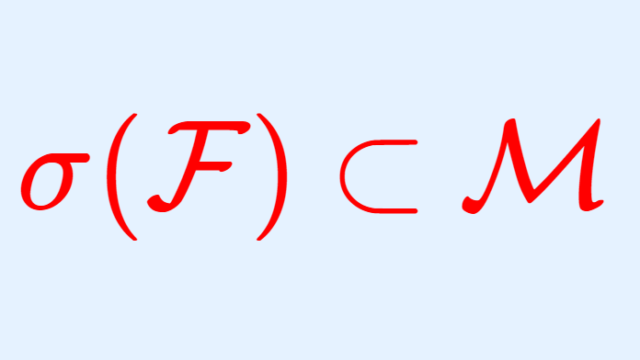 測度論
測度論 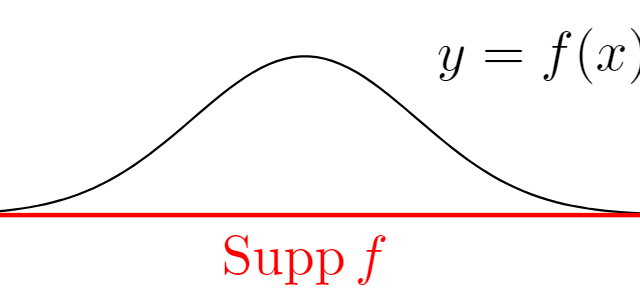 記号・記法
記号・記法  測度論
測度論 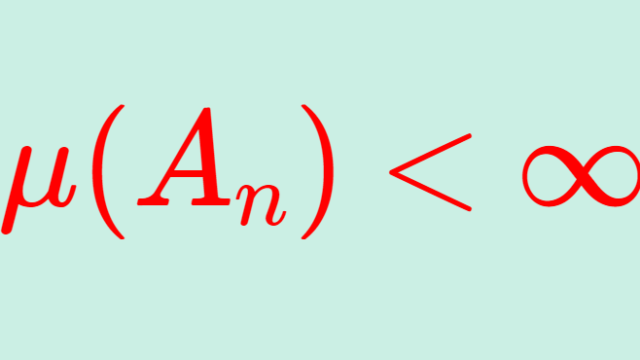 測度論
測度論 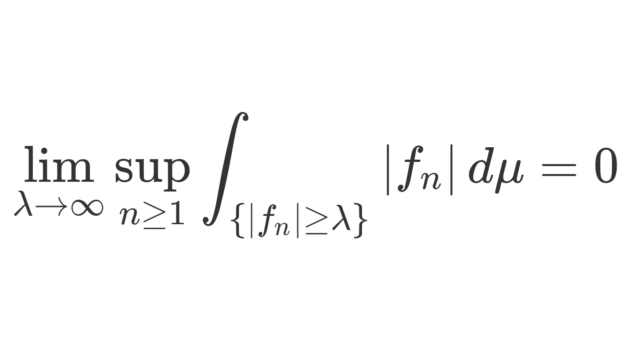 測度論
測度論 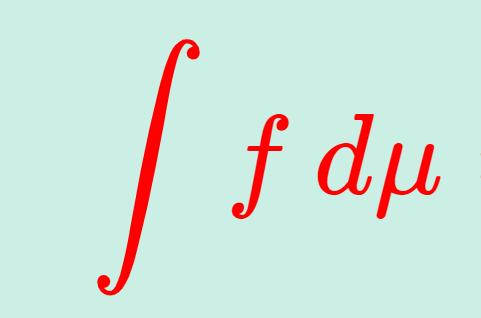 測度論
測度論 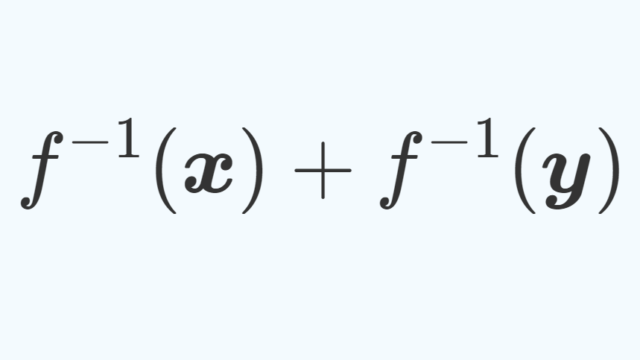 線形代数学
線形代数学 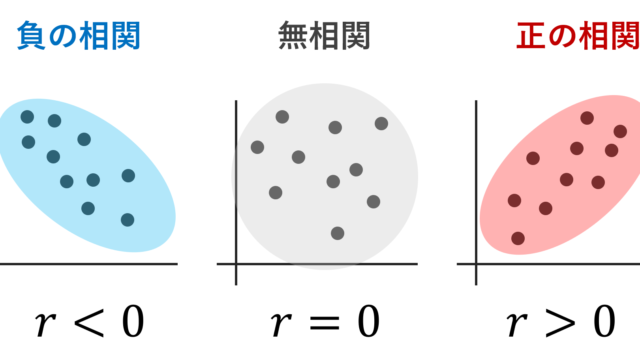 統計学
統計学