 統計学
統計学 度数分布表とは~定義と関連用語をまとめて図解~
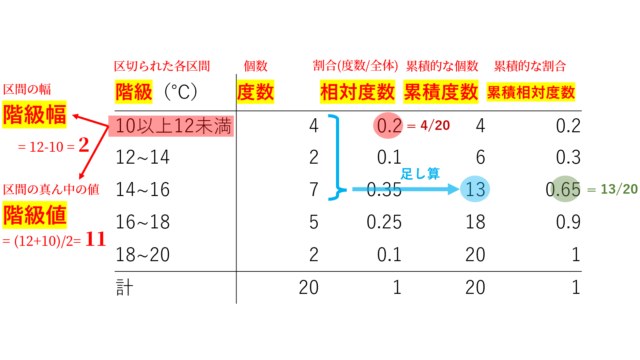
統計学における,データをまとめる手法として「度数分布表」と,その関連用語を図を使って紹介しましょう。データをある範囲ごとに区切って,その範囲に属する数の散らばりの様子を度数分布 (frequency distribution) といい,それを表にしたものを度数分布表 (frequency table) という。
 統計学
統計学  群・環・体
群・環・体 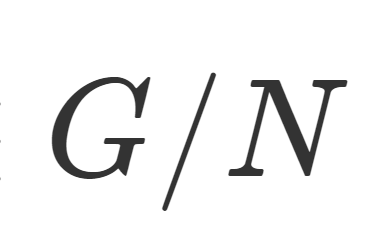 群・環・体
群・環・体 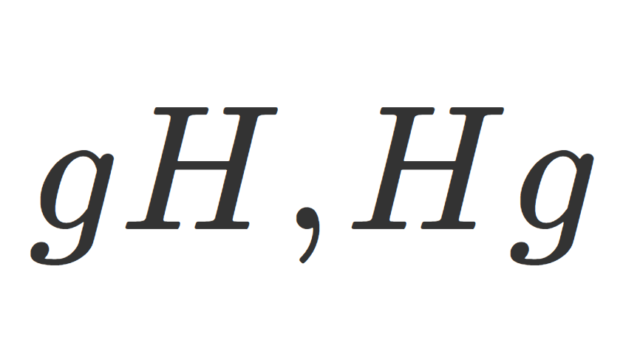 群・環・体
群・環・体 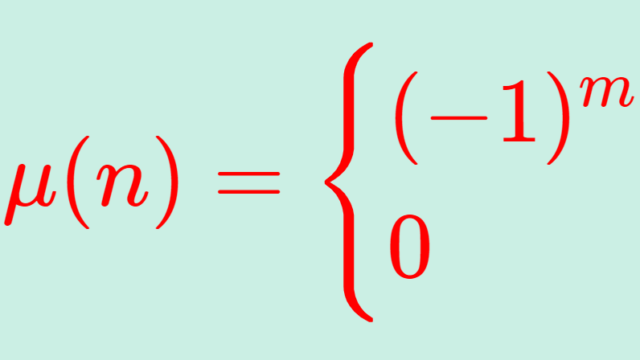 数論
数論 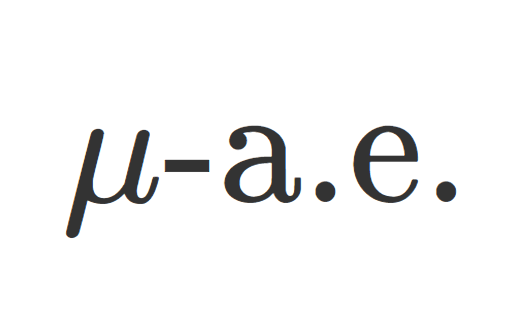 測度論
測度論 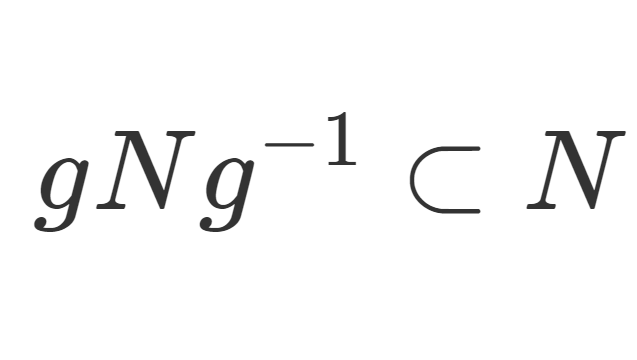 群・環・体
群・環・体 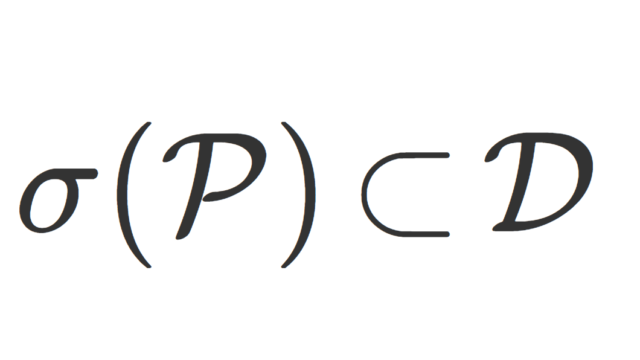 測度論
測度論 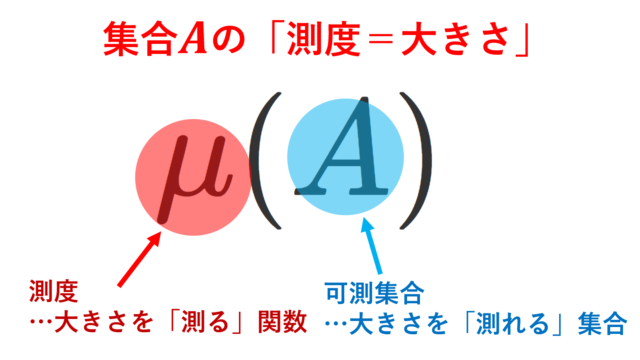 測度論
測度論  統計学
統計学