 線形代数学
線形代数学 基底の変換行列とは~定義と性質をわかりやすく~
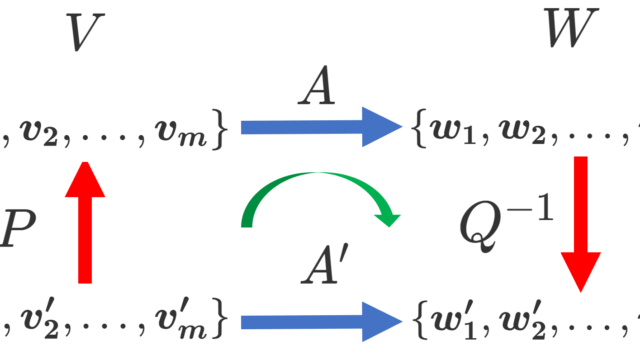
有限次元ベクトル空間において,別の2つの基底を取ったときに,その関係性を述べる「基底の変換行列」について,その定義と性質を分かりやすく紹介します。「線形写像の表現行列」との比較も行います。
 線形代数学
線形代数学 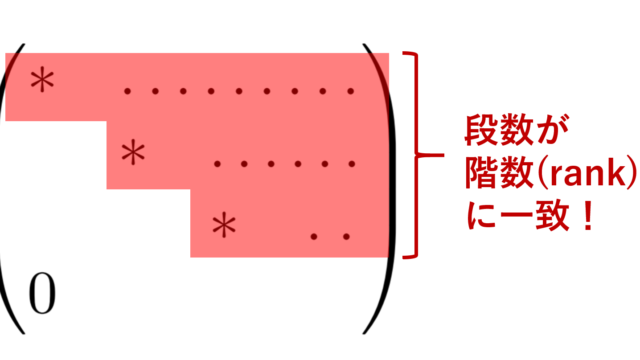 線形代数学
線形代数学 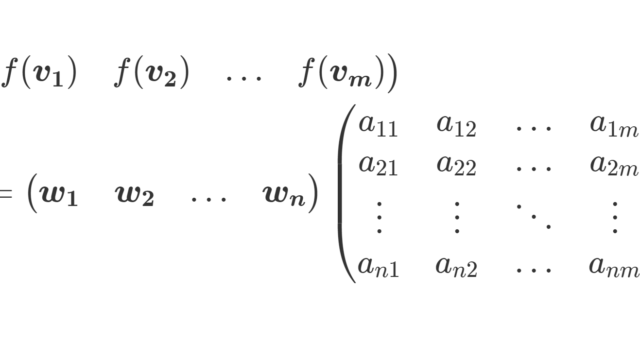 線形代数学
線形代数学 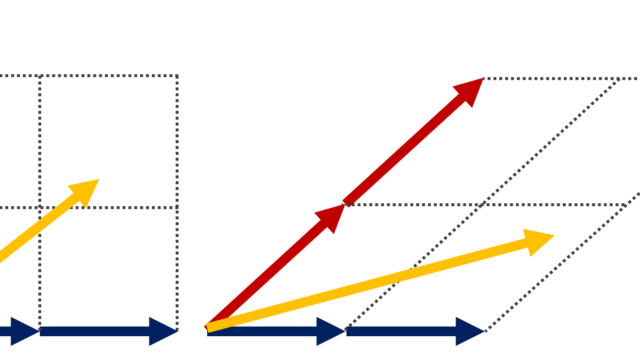 線形代数学
線形代数学  線形代数学
線形代数学 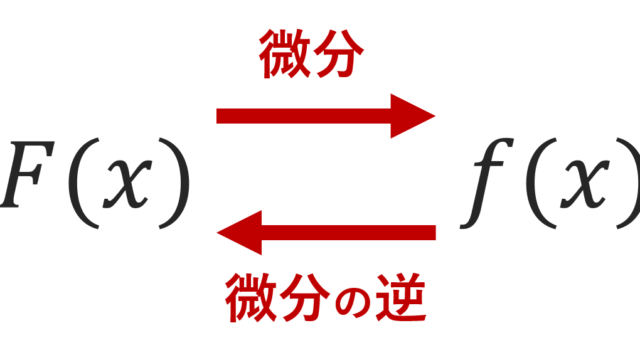 微分積分学(大学)
微分積分学(大学) 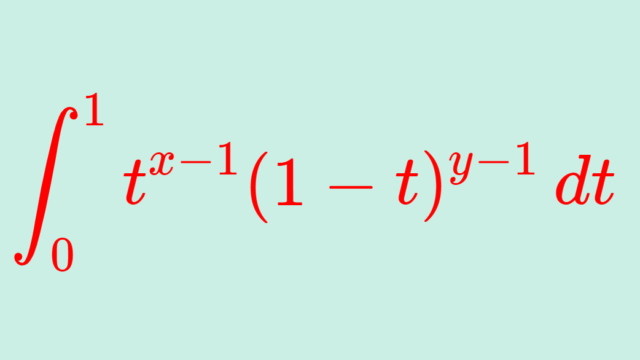 微分積分学(大学)
微分積分学(大学) 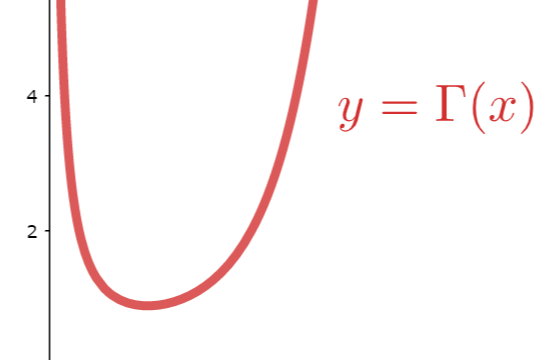 微分積分学(大学)
微分積分学(大学) 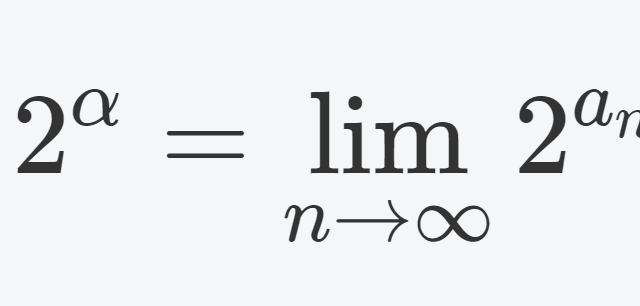 記号・記法
記号・記法 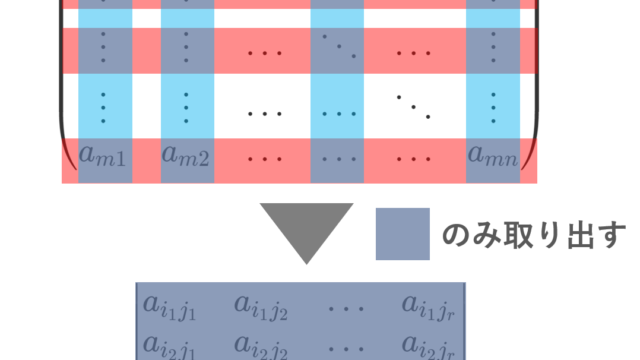 線形代数学
線形代数学