線形代数学 ベクトルの一次独立・一次従属の定義と具体例6つ
ベクトルにおける一次独立・一次従属は，大学数学における難しい概念の1つでしょう。これについて，詳しく掘り下げ，具体例も多く確認していきましょう。高校生でも，ある程度は理解できると思います。
用語・記号の定義
線形代数学 
微分積分学(大学) 原始関数・不定積分の厳密な定義とその違い
ときに出てくる2つの言葉である「原始関数」と「不定積分」について，その専門数学における厳密な定義と違いについて述べ，理解を深めましょう。おいては，原始関数と不定積分は同じものと定義されます。今回はその立場を取らず，原始関数と不定積分は違うものとして定義します。
微分積分学(大学) ベータ関数とは～定義と性質8つとその証明～
ベータ関数 （beta function) とは，B(x,y) = ∫_0^1 t^{x-1} (1-t)^{y-1} dt と定義される特殊関数です。これについて，その定義と性質とその証明を行いましょう。
微分積分学(大学) ガンマ関数とは～定義と性質をわかりやすく～
階乗の一般化であり，解析学でよく使われる関数であるガンマ関数 (Gamma function) について，その定義と性質を詳しく述べましょう。
記号・記法 【数学】well-defined, ill-definedとは
数学における well-defined, ill-defined とは，それぞれ「ちゃんと定義できている」，「定義があいまい・無効・無意味である」ことを意味します。この言葉について，具体例も交えながら，分かりやすく紹介しましょう。
線形代数学 小行列式とは
m×n行列における小行列式とは，いくつかの行・列を同じ数だけ取り出して，それのみ並べ直したr次正方行列の行列式(det)のことを指します。このことについて，定義と，元の行列の階数(ランク)との関係，また余因子との関係も述べましょう。
線形代数学 余因子行列の定義と余因子展開～逆行列になる証明～
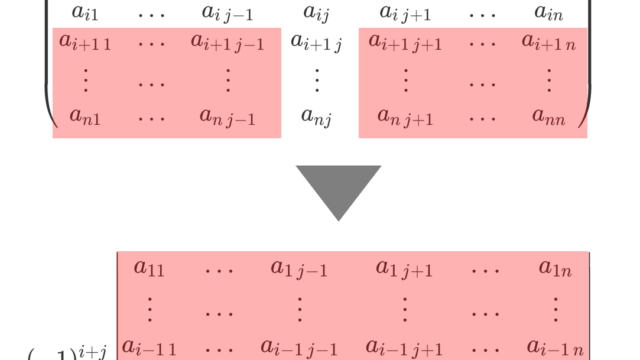
余因子 (cofactor)・余因子行列 (adjugate matrix) の定義と余因子展開について図解付きで述べ，余因子行列が逆行列の行列式倍になることの証明を行いましょう。
確率論 コーシー分布の定義と性質とその証明
コーシー分布 (Cauchy distribution) は，期待値が定義できず，正規分布より減衰が遅い，裾の厚い分布（裾の重い分布）として有名です。確率密度関数はp(x) = 1/π(x^2+1)となります。これについて，その定義と性質の証明を詳しく述べましょう。
集合と位相 可算集合と非可算集合(可算無限・非可算無限)
専門数学を理解するにあたって重要な概念の一つの「無限の大小」について，すなわち可算集合（countable set, 可算無限）と非可算集合（非可算無限）について，その定義と性質を紹介しましょう。非可算集合については，連続体濃度を扱います。
集合と位相 集合の濃度をわかりやすく丁寧に
集合の「濃度 (cardinality) 」とは，集合の要素の個数の概念を，無限個の集合についても適用できるよう一般化したものです。これの定義について，分かりやすく丁寧に説明していきましょう。