 集合と位相
集合と位相 位相空間における連続写像の定義と性質を詳しく
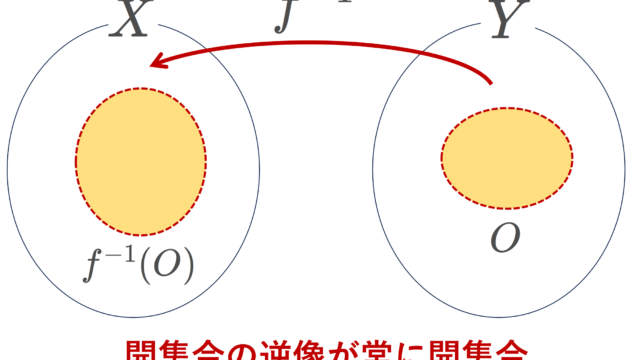
位相空間における連続写像とは,「開集合の逆像が開集合」になるという風に定義されます。まずは,連続写像の定義と,それと同値な性質について,証明付きで紹介し,さらに今までの連続性の定義のベースであった,イプシロンデルタ論法との定義の一貫性を確認します。その後,その他の性質もたくさん述べます。
 集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 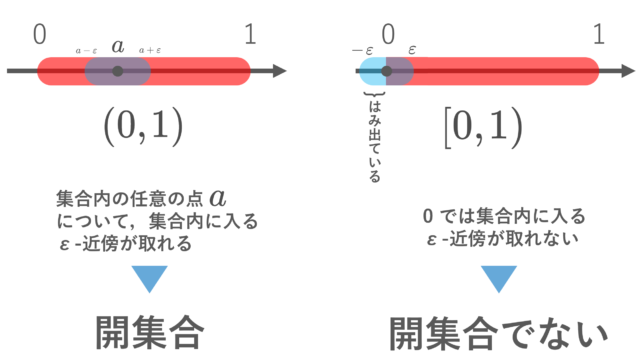 集合と位相
集合と位相 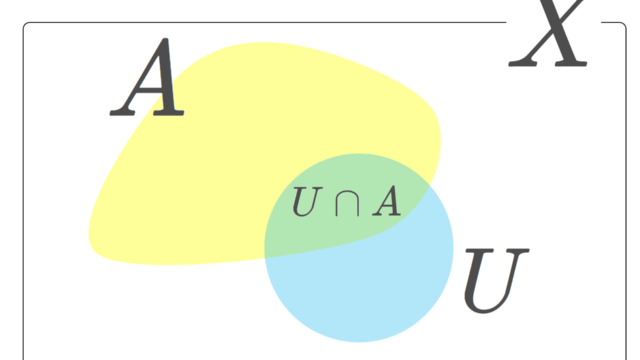 集合と位相
集合と位相 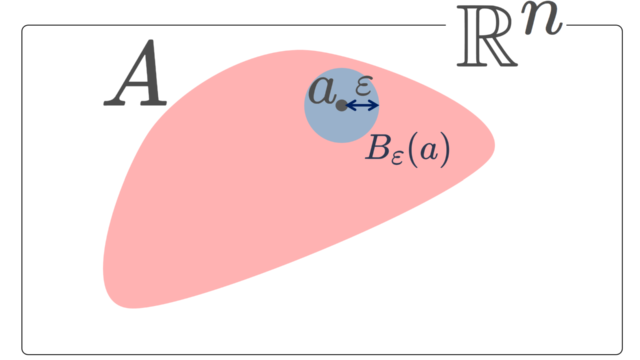 集合と位相
集合と位相 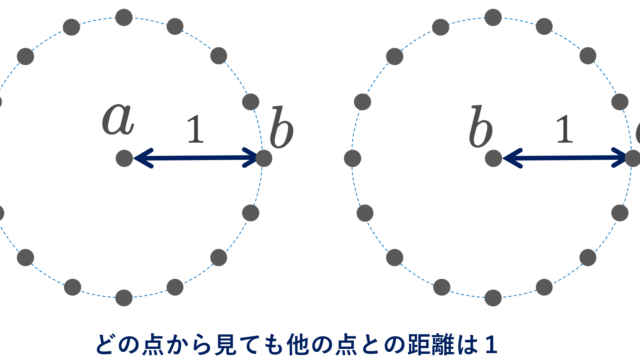 集合と位相
集合と位相