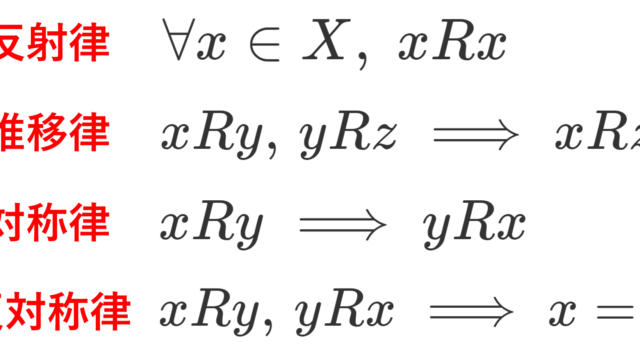 集合と位相
集合と位相 反射律・推移律・対称律・反対称律の定義と具体例7つ
二項関係 (binary relation) の性質である,反射律 (reflexive)・推移律 (transitive)・対称律 (symmetric)・反対称律 (antisymmetric) の定義と具体例7つを紹介します。
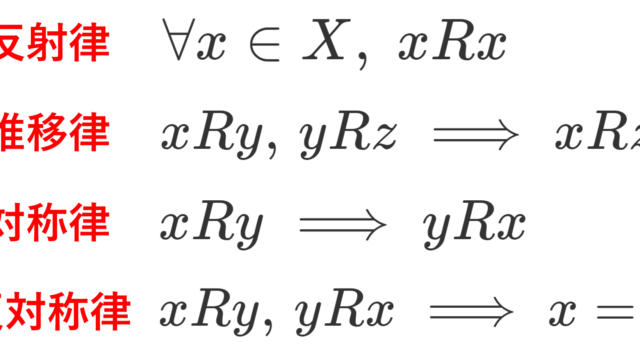 集合と位相
集合と位相 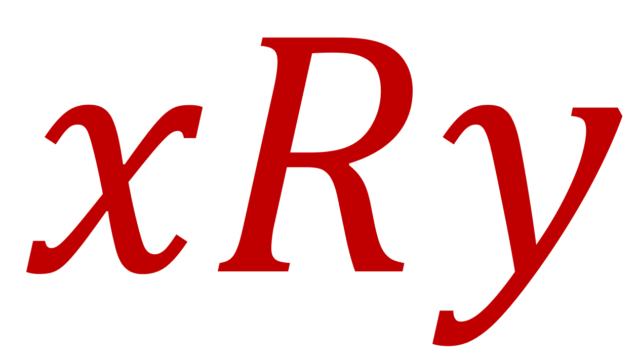 集合と位相
集合と位相  解析学(大学)その他
解析学(大学)その他  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  線形代数学
線形代数学 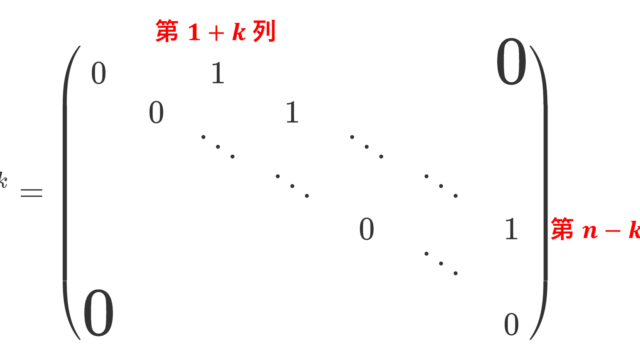 線形代数学
線形代数学 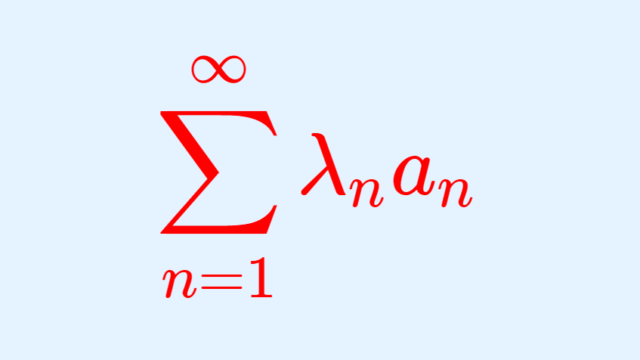 微分積分学(大学)
微分積分学(大学)  集合と位相
集合と位相  微分積分学(大学)
微分積分学(大学)