 線形代数学
線形代数学 固有値の定義と求め方をていねいに~計算の手順~
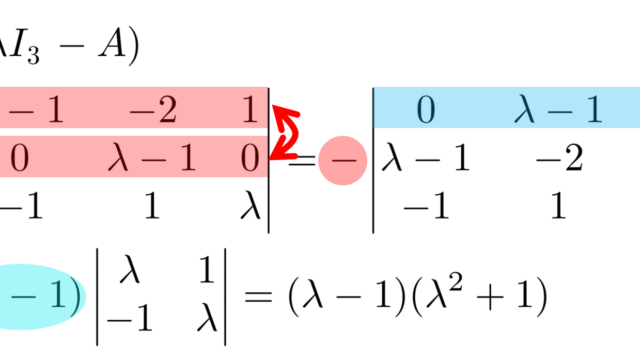
固有値 (eigenvalue) の定義とその求め方(計算手順)について,例題も交えて詳細に解説しましょう。検算方法についても紹介します。
 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学 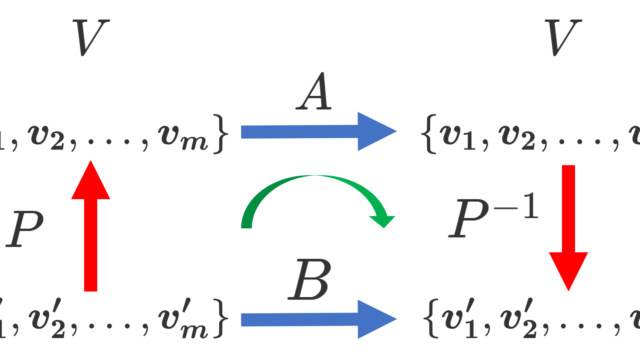 線形代数学
線形代数学 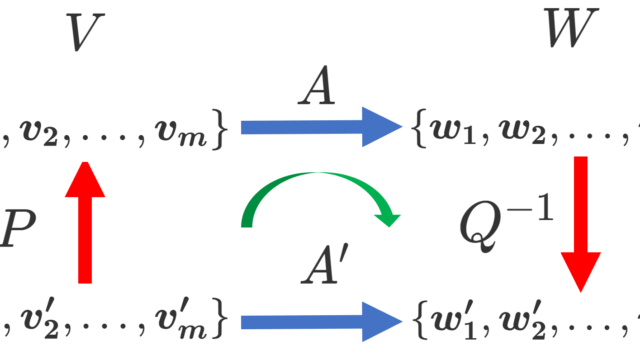 線形代数学
線形代数学 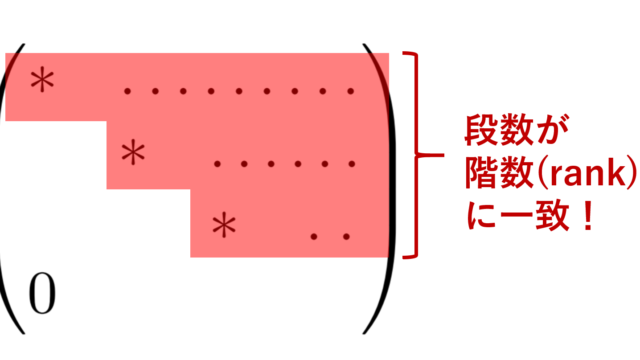 線形代数学
線形代数学 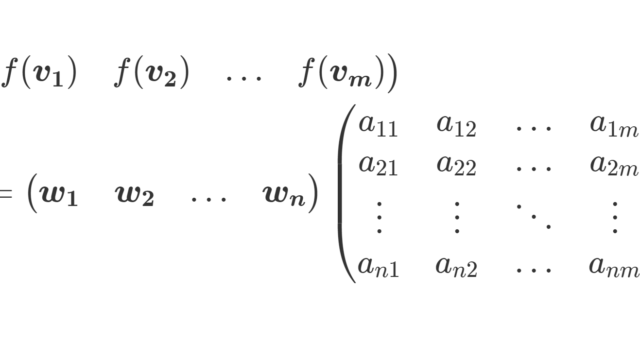 線形代数学
線形代数学 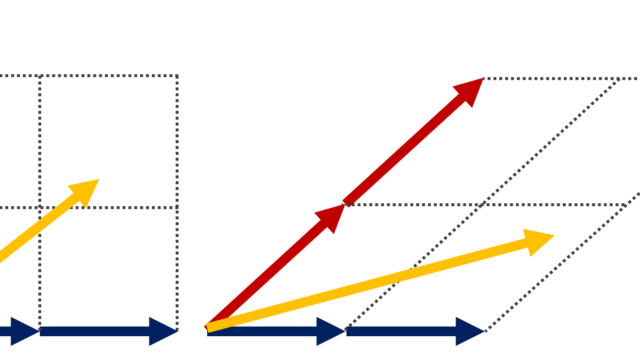 線形代数学
線形代数学 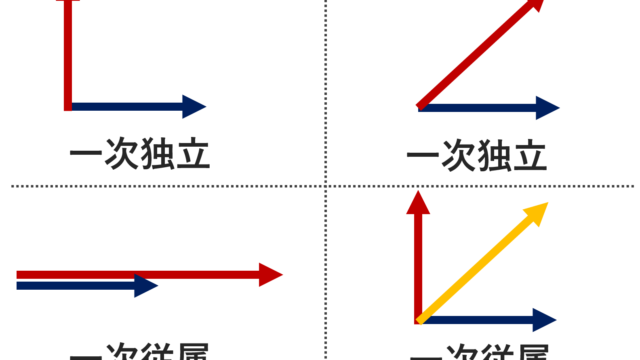 線形代数学
線形代数学