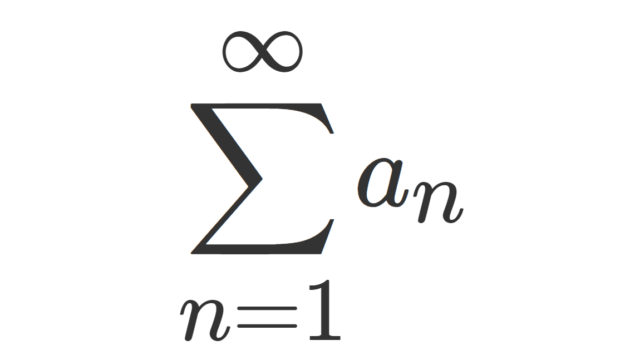 微分積分学(大学)
微分積分学(大学) 級数の収束・発散判定法13個まとめ
級数の収束判定法・発散判定法は,さまざまなものが知られています。これについて,有名な13個をまとめましょう
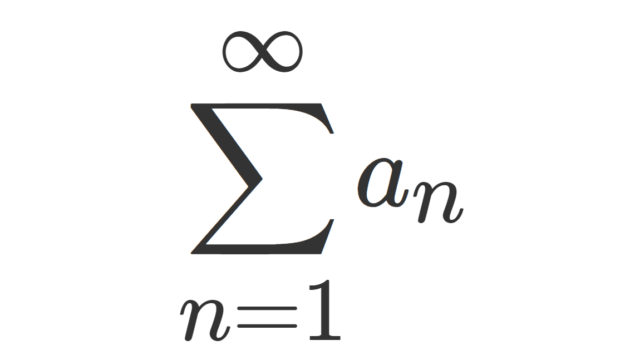 微分積分学(大学)
微分積分学(大学) 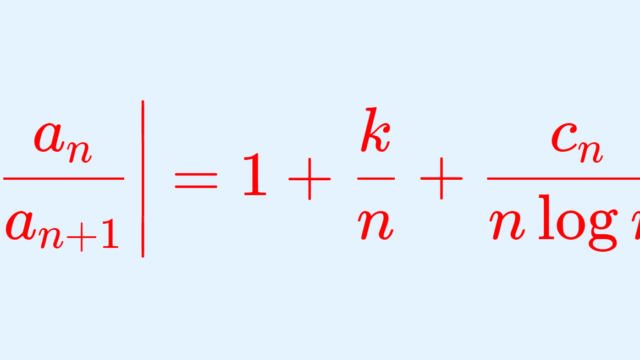 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学) 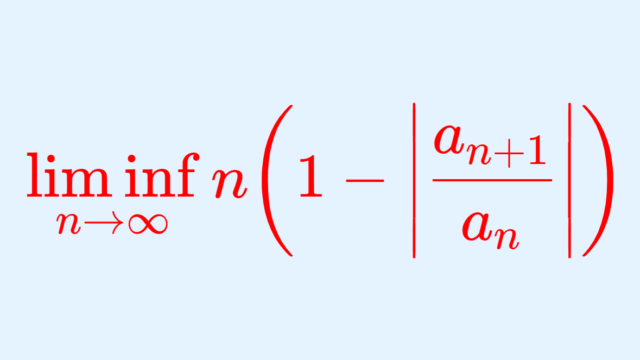 微分積分学(大学)
微分積分学(大学) 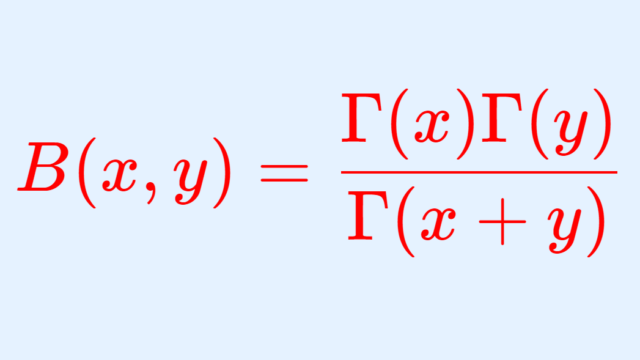 微分積分学(大学)
微分積分学(大学) 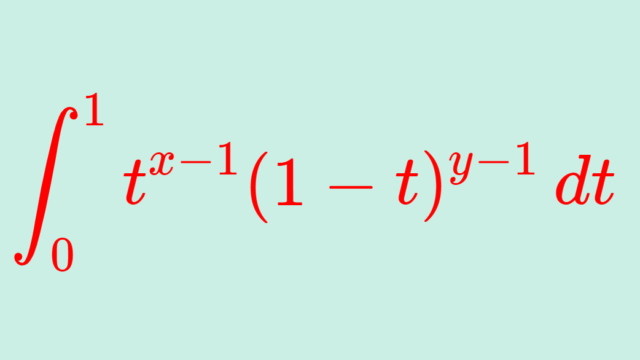 微分積分学(大学)
微分積分学(大学) 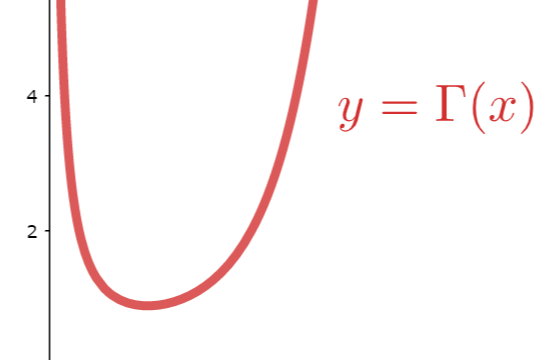 微分積分学(大学)
微分積分学(大学) 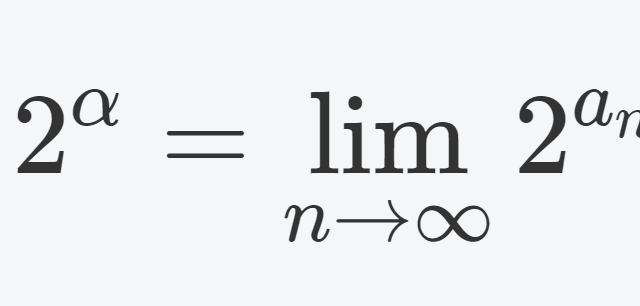 記号・記法
記号・記法 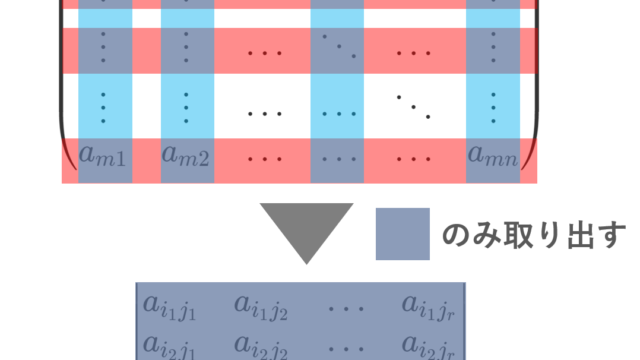 線形代数学
線形代数学 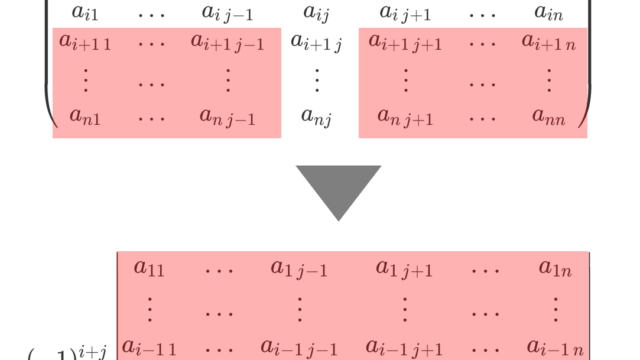 線形代数学
線形代数学