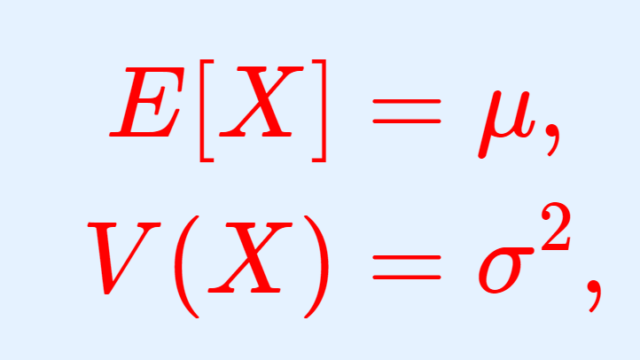 確率論
確率論 正規分布の期待値(平均)・分散・標準偏差とその導出証明
正規分布の期待値(平均)・分散・標準偏差について,その導出の証明を行います。「定義から直接証明する方法」と「特性関数の微分を用いた方法」の2通りで証明しましょう。
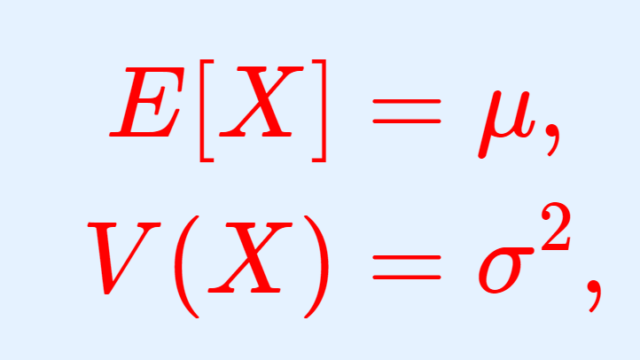 確率論
確率論 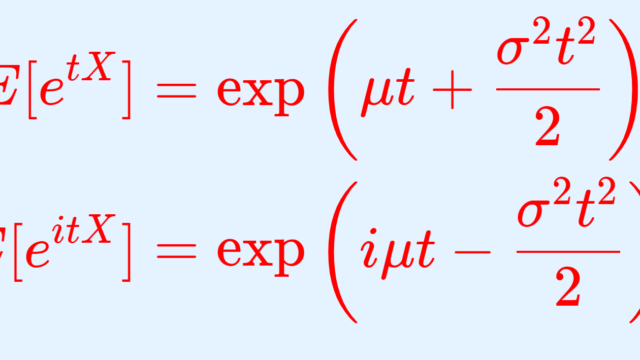 確率論
確率論 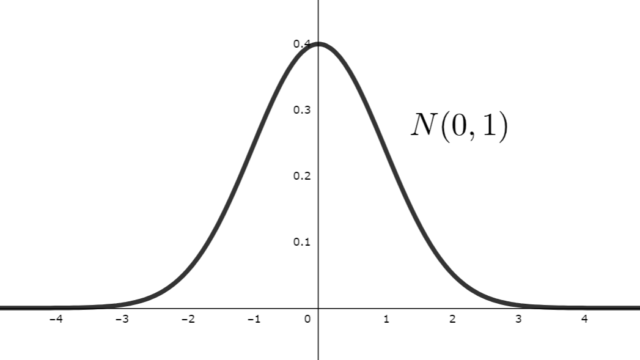 確率論
確率論 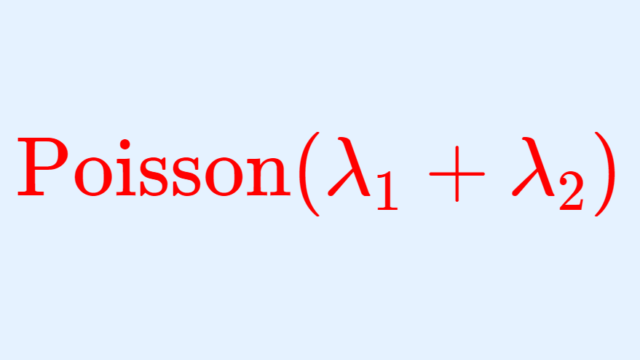 確率論
確率論 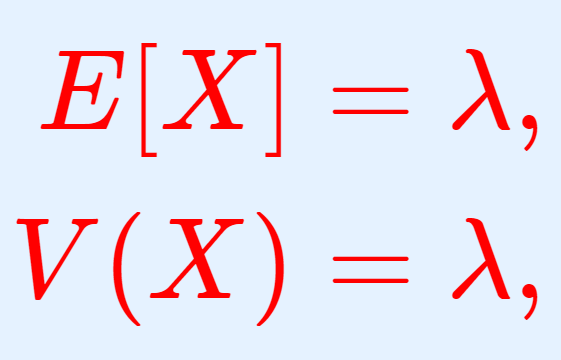 確率論
確率論 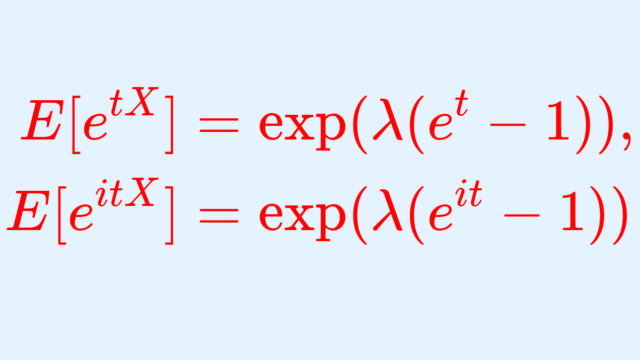 確率論
確率論 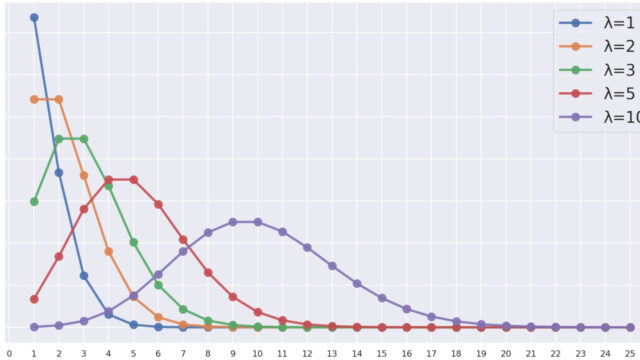 確率論
確率論 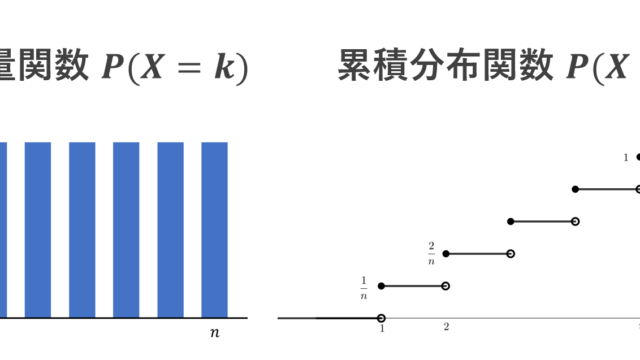 確率論
確率論 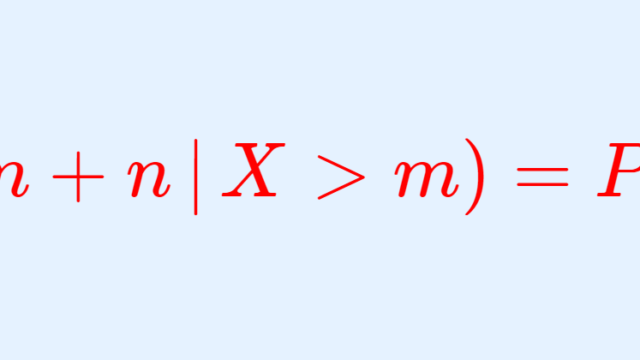 確率論
確率論 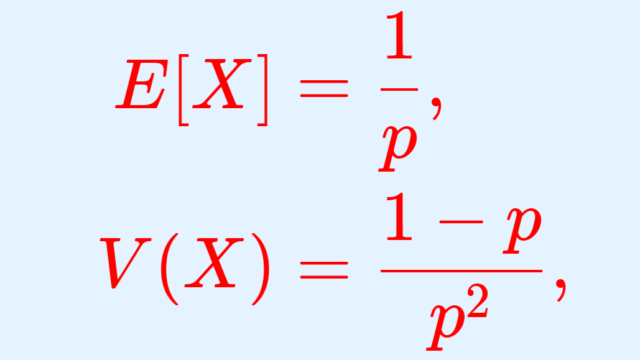 確率論
確率論