 確率論
確率論 ベルヌーイ分布とは~定義と性質の導出~
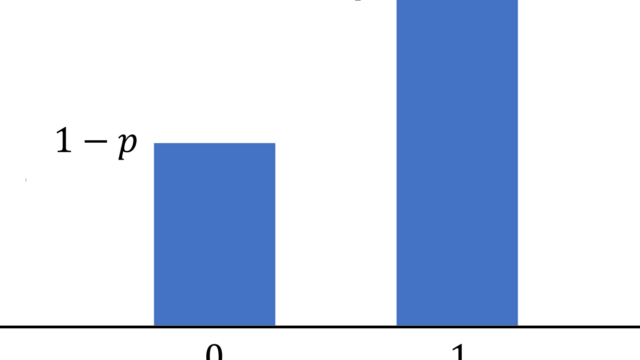
ベルヌーイ分布 (Bernoulli distribution) は,ある確率pで1を,残りの確率1-pで0となるような確率分布のことです。これについて,その定義と性質(平均・分散・標準偏差・積率母関数・特性関数など)を述べましょう。
 確率論
確率論  確率論
確率論  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学) 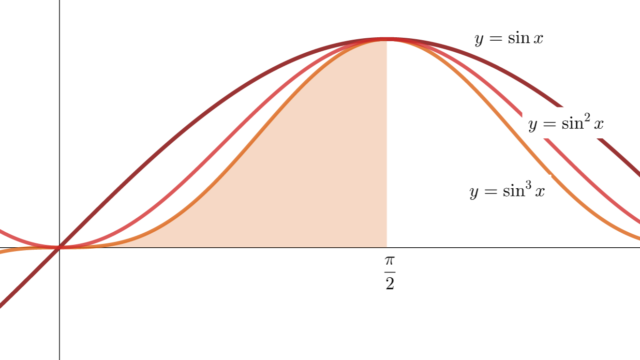 微分積分学(大学)
微分積分学(大学) 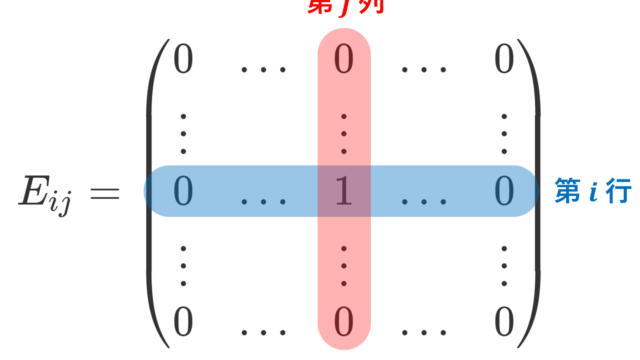 線形代数学
線形代数学 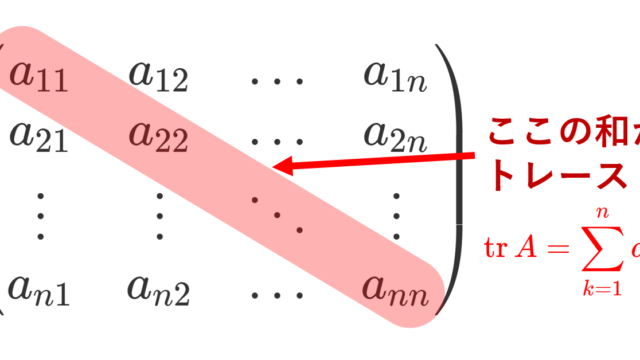 線形代数学
線形代数学 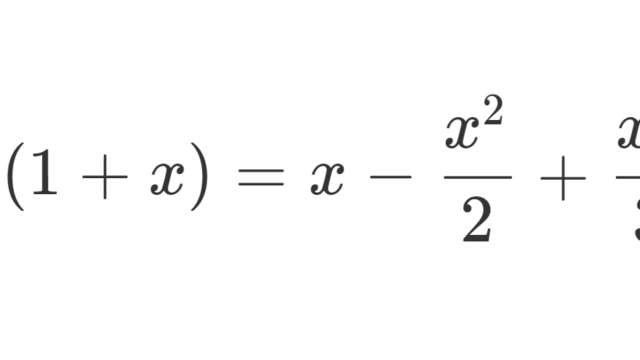 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)