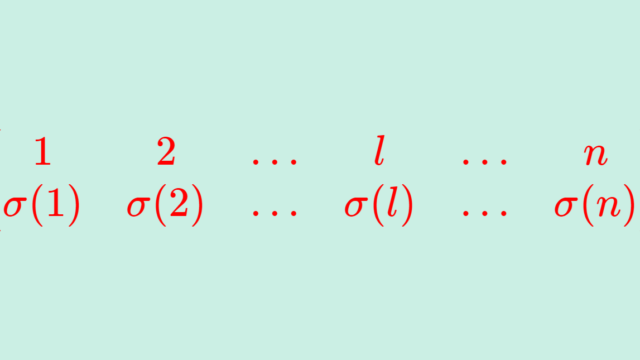 線形代数学
線形代数学 線形代数(行列)における置換・奇置換・偶置換の最低限必要な知識
線形代数学や群論において登場する「置換 (permutation) 」やその関連概念である置換の積・奇置換・偶置換・互換・逆置換・置換の符号について,特に線形代数の行列式を定義するにあたって必要な知識のみをまとめて解説します。
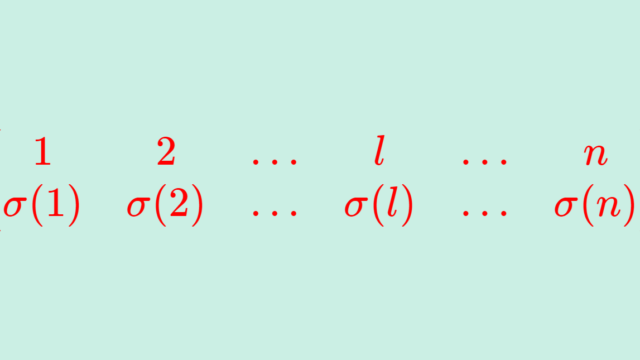 線形代数学
線形代数学  微分積分学(大学)
微分積分学(大学)  集合と位相
集合と位相 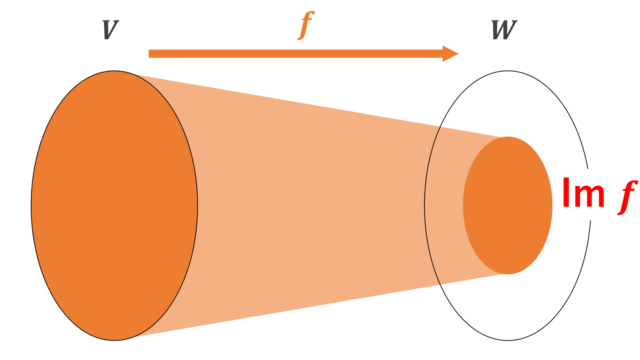 線形代数学
線形代数学 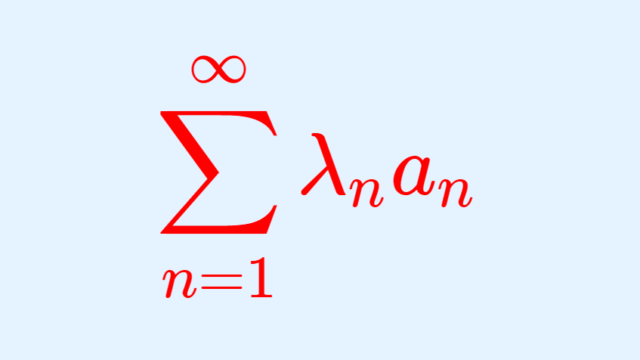 微分積分学(大学)
微分積分学(大学) 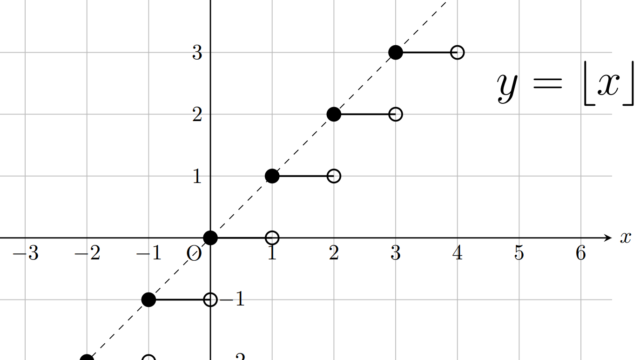 記号・記法
記号・記法 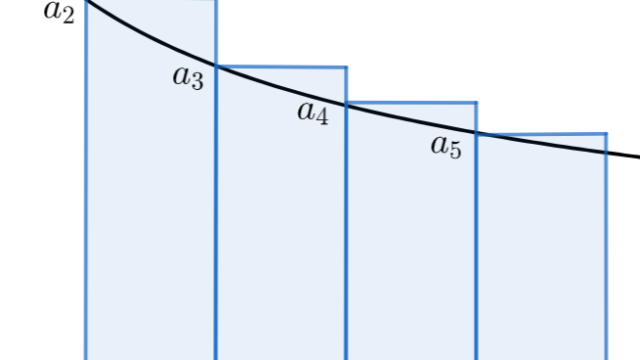 微分積分学(大学)
微分積分学(大学) 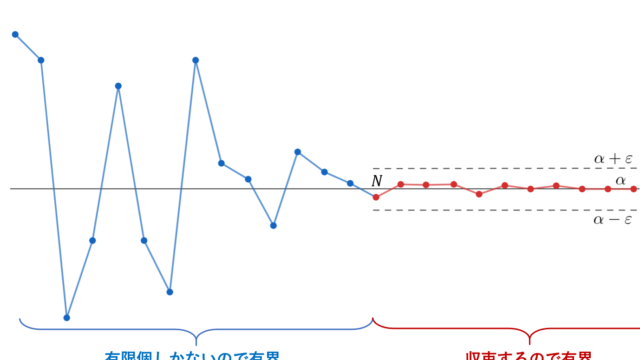 微分積分学(大学)
微分積分学(大学) 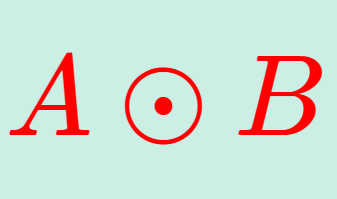 線形代数学
線形代数学 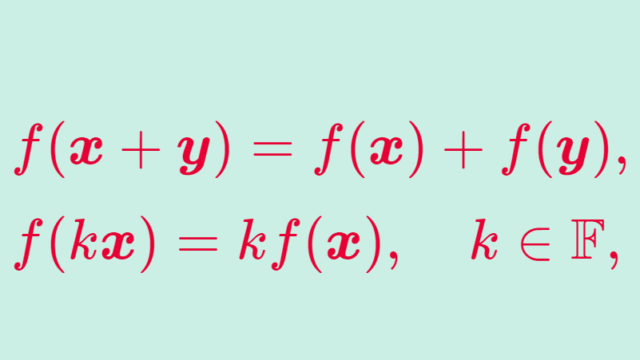 線形代数学
線形代数学