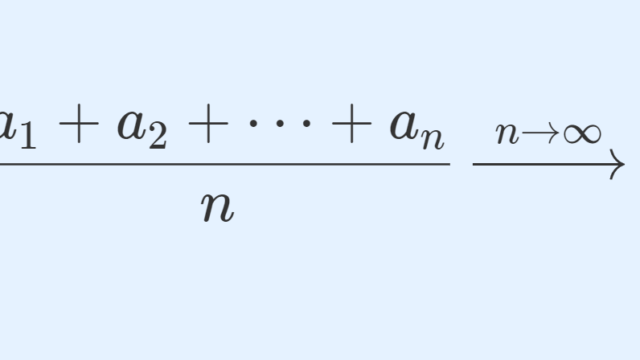 微分積分学(大学)
微分積分学(大学) 【チェザロ平均】数列が収束するとき平均も同じ値に収束する証明
ε-δ論法を習った後によく出てくる有名な定理の一つとして,「数列が収束すれば平均も同じ値に収束する」というものがあります。これについて紹介します。相加平均の定理はもちろん,相乗平均に関する定理も紹介します。
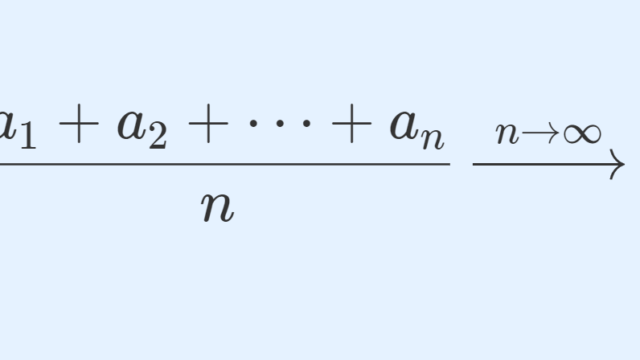 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学) 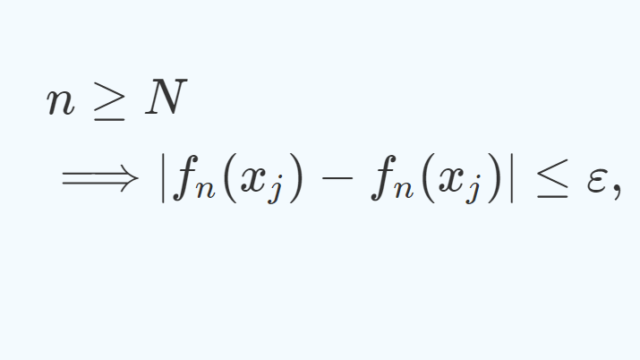 微分積分学(大学)
微分積分学(大学) 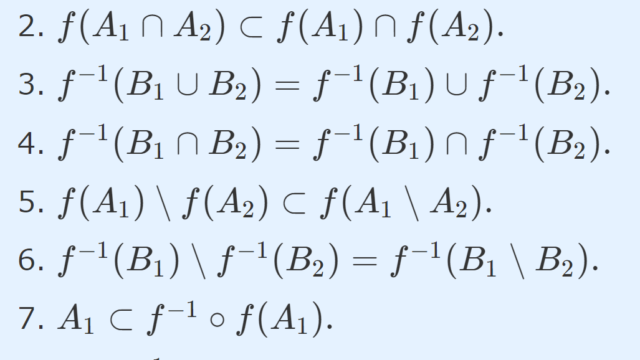 集合と位相
集合と位相 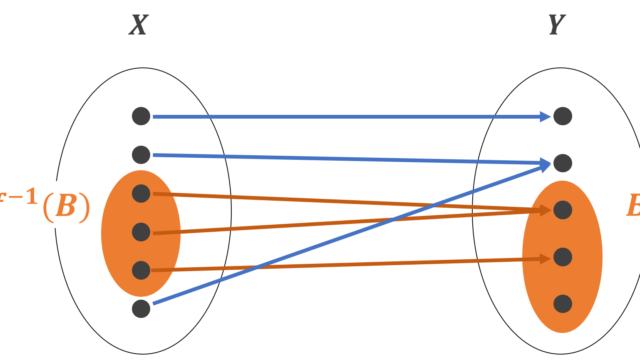 記号・記法
記号・記法 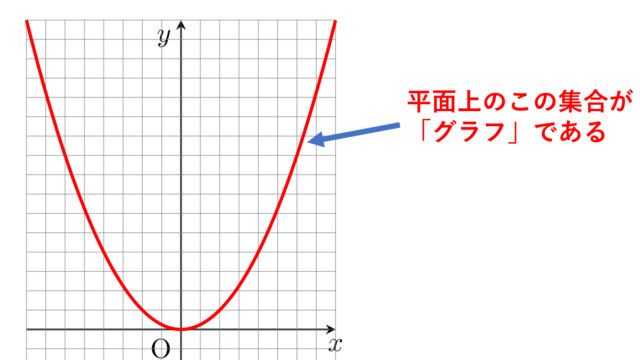 記号・記法
記号・記法 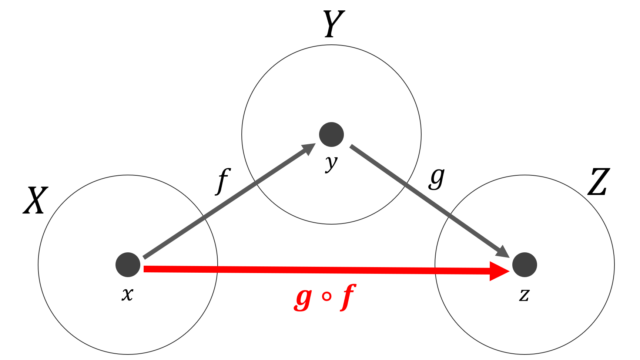 記号・記法
記号・記法 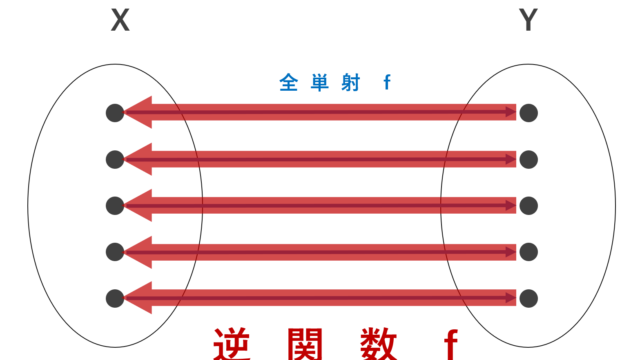 記号・記法
記号・記法 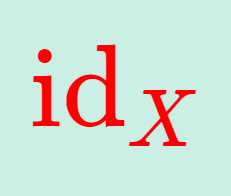 記号・記法
記号・記法