 解析学(大学)その他
解析学(大学)その他 デデキント切断による実数の構成を解説
デデキント切断をざっくり説明すると,有理数のみの数直線を2つに切断して,その「切り口」を新たに数と思うことで,実数を定義しようというものです。これにより,有理数にはない「実数の連続性」が成り立ちます。デデキント切断について,その定義から実数の定義を紹介し,さらに実数の連続性について述べ,実数の演算を定義していきましょう。
 解析学(大学)その他
解析学(大学)その他  集合と位相
集合と位相  集合と位相
集合と位相  集合と位相
集合と位相 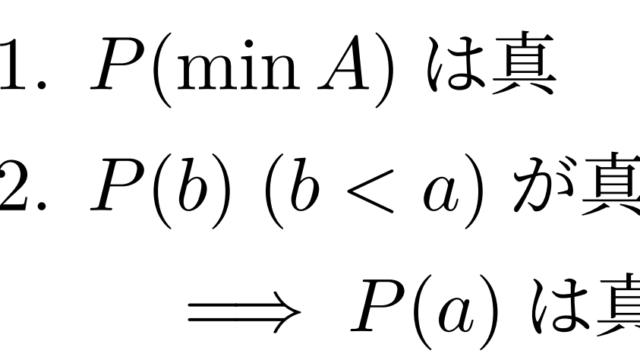 集合と位相
集合と位相 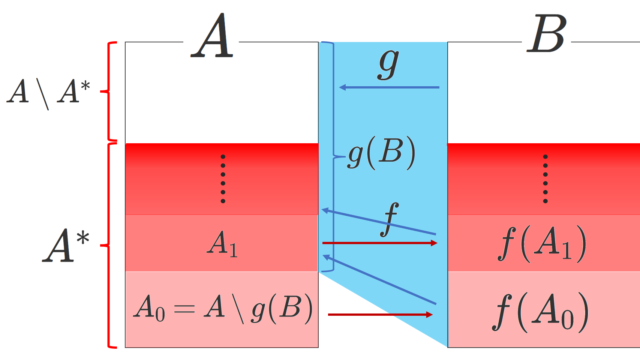 集合と位相
集合と位相 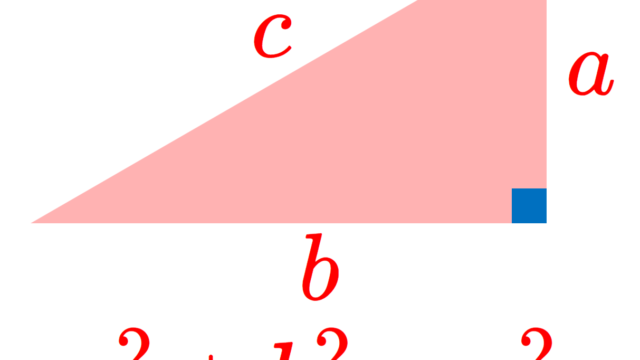 数論
数論 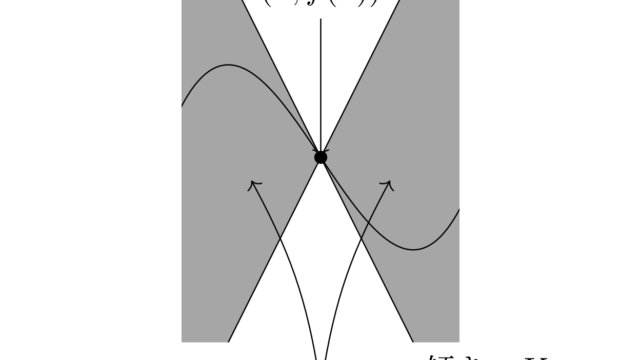 解析学(大学)その他
解析学(大学)その他  群・環・体
群・環・体  群・環・体
群・環・体