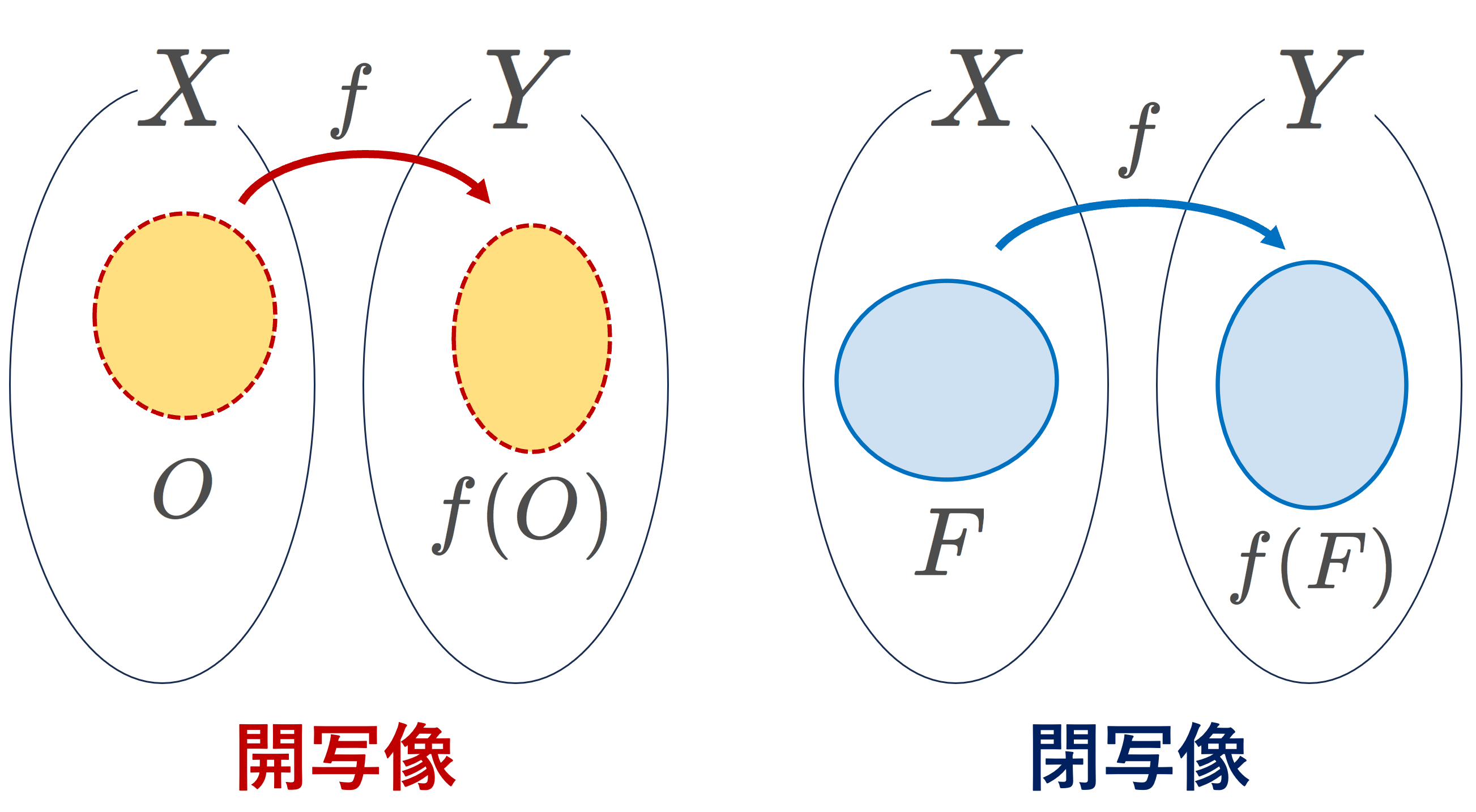
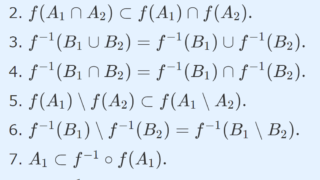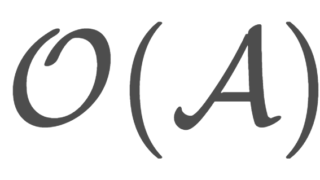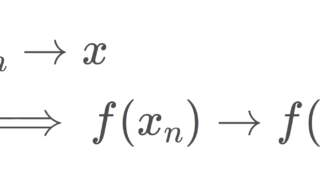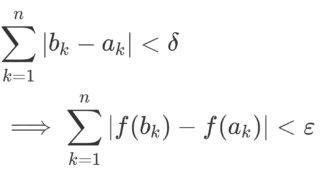位相空間における連続写像とは,「開集合の逆像が開集合になる」という風に定義されます。まずは,連続写像の定義と,それと同値な性質について,証明付きで紹介します。さらに,今までの連続性の定義のベースであった,イプシロンデルタ論法との定義の一貫性を確認します。その後,その他の性質もたくさん述べます。
位相空間における連続写像
位相空間における連続写像の定義,定義と同値な性質5つ,連続写像の具体例6つを紹介しましょう。
連続写像の定義
定義1(開集合を用いた連続写像の定義)
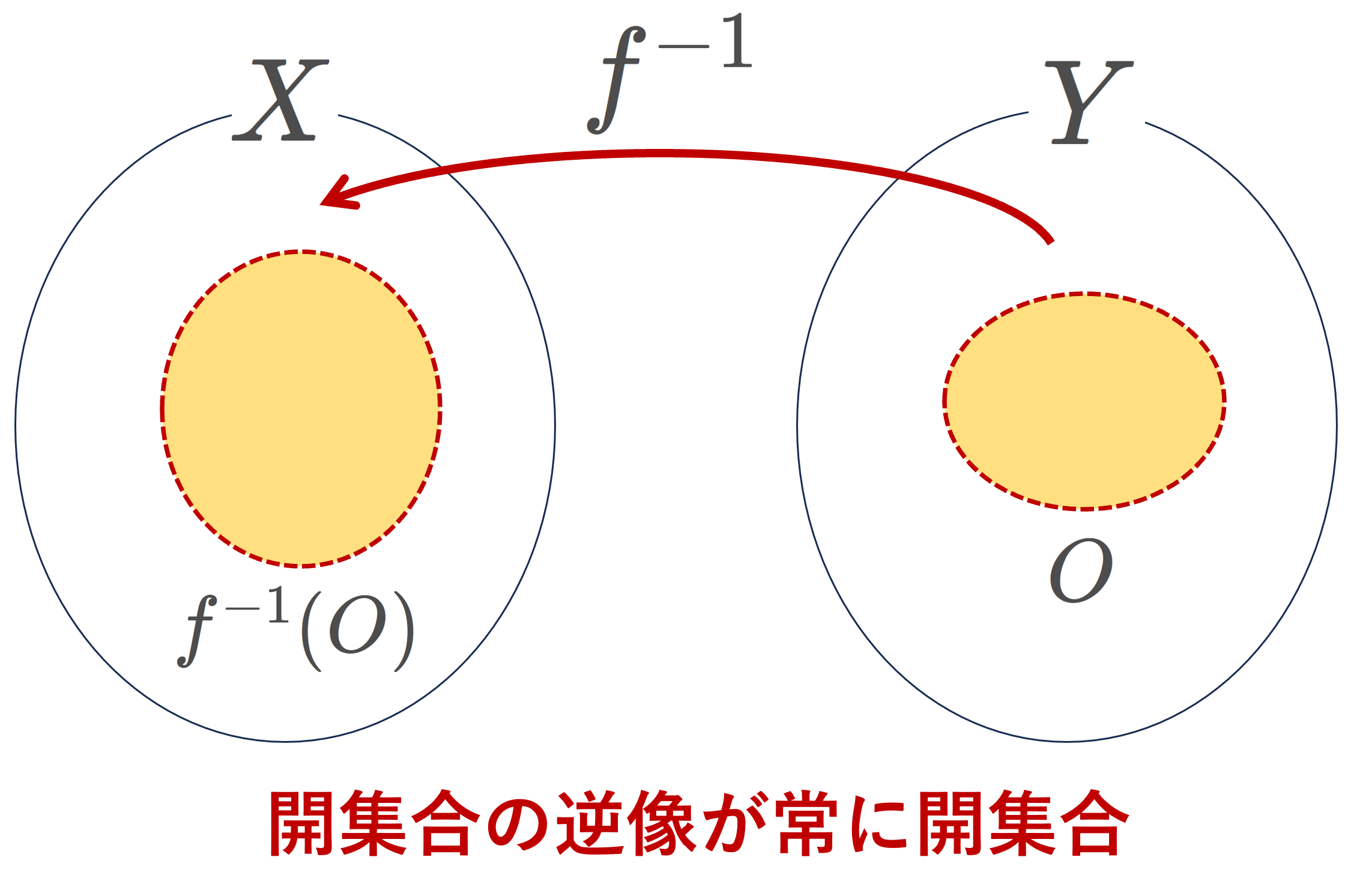
(X,\mathcal{O}_X), (Y,\mathcal{O}_Y) を位相空間とする。 f\colon X\to Y が連続写像 (continuous mapping) であるとは,
\Large \color{red} O\in \mathcal{O}_Y\implies f^{-1}(O)\in \mathcal{O}_X
が成り立つことをいう。
日本語で述べると,開集合の逆像が常に開集合になるような写像のことを連続写像というんですね。 f^{-1}(O)= \{ x\in X\mid f(x)\in O\} です。
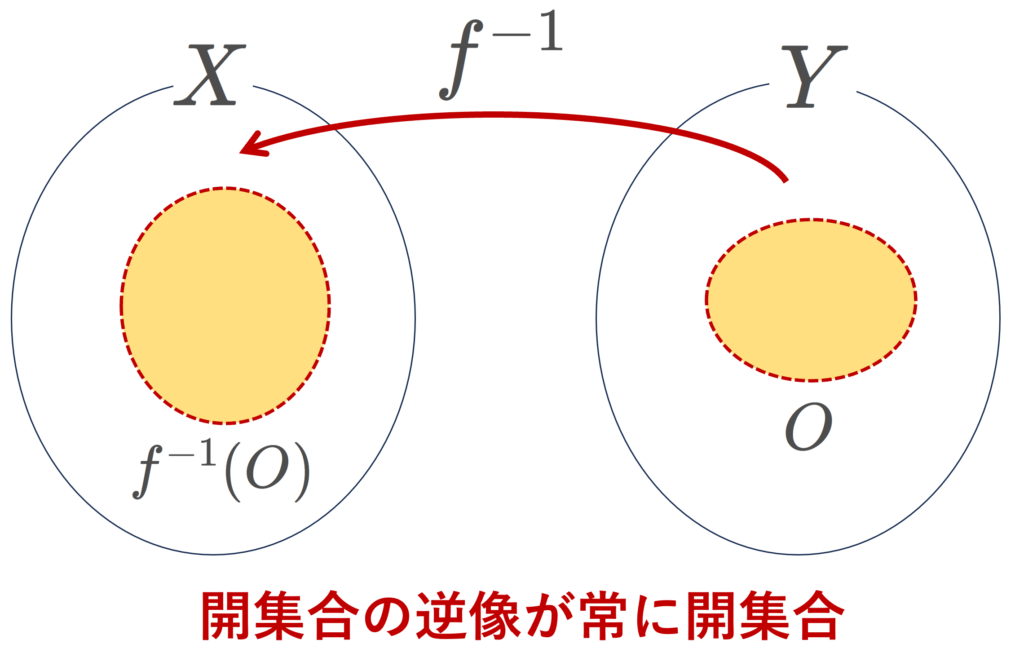
位相空間 (X,\mathcal{O}_X) から (Y,\mathcal{O}_Y) への写像は,単に f\colon X\to Y とかく他に,位相を明示して f\colon (X,\mathcal{O}_X)\to (Y, \mathcal{O}_Y) とかくことがあります。後の具体例で使います。
ユークリッド空間や距離空間における連続写像の定義とは大きく異なっており,少々驚いたかもしれません。しかし,ユークリッド空間や距離空間における連続写像の定義ときちんと一貫性があります。これについては,あとに述べることにして,とりあえず先に一つだけ例を紹介しましょう。
例1(連続写像の例).
実数全体の集合 \R に通常の位相を入れた位相空間について, f,g, h\colon \R\to\R を考える。
- f(x)= x^2 は連続である
- g(x)=\max\{ 0, x\} は連続である
- h(x)= \begin{cases} 1 & x\ge 0, \\ 0 & x< 0\end{cases} は連続でない

f, g に関しては,たとえば
\begin{aligned} f^{-1}((1, 4))&= (-2,-1)\cup(1,2), \\ f^{-1} ((-2, 1)) &= (-1, 1), \\ f^{-1}((-\infty, 0)) &= \emptyset, \\ g^{-1}((1,2)) &= (1,2), \\ g^{-1}((-1, 1)) &= (-\infty, 1), \\ g^{-1} ((-2, 0)) &= \emptyset \end{aligned}
なので,ちゃんと開集合の逆像が開集合になっていますね。一方で,
であり,一つ目の例は開集合の逆像が開集合になっていませんね。他にもいろいろな例を自分で考えてみてください。
連続写像の定義の同値性
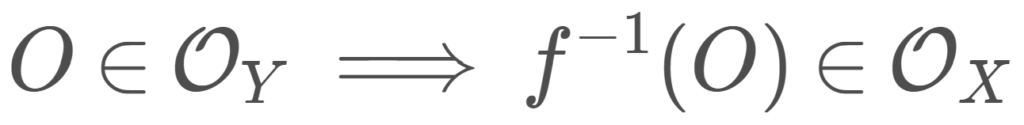
さて,上のように,開集合を用いて連続写像の定義をしましたが,他にも同値な定義があります。
定理1(連続写像の同値な定義)
(X,\mathcal{O}_X), (Y,\mathcal{O}_Y) を位相空間とし, f\colon X\to Y とする。このとき,以下は同値である。
- O\in \mathcal{O}_Y\implies f^{-1}(O)\in \mathcal{O}_X,すなわち,開集合の逆像が開集合になる(連続写像の定義)
- 任意の \mathcal{O}_Y-閉集合 F\subset Y に対し, f^{-1}(F)\subset X が \mathcal{O}_X-閉集合になる。すなわち,閉集合の逆像が閉集合になる
- 任意の x\in X に対し, f(x) の任意の近傍 N\subset Y の逆像 f^{-1}(N)\subset X が x の近傍になる
- 任意の部分集合 B\subset Y に対し, f^{-1}(\operatorname{Int}(B))\subset \operatorname{Int}(f^{-1}(B)) となる
- 任意の部分集合 A\subset X に対し, f(\overline{A})\subset \overline{f(A)} となる
- \mathcal{S}_Y を (Y,\mathcal{O}_Y) の準開基としたとき, S\in \mathcal{S}_Y\implies f^{-1}(S)\in \mathcal{O}_X,すなわち,準開基の元の逆像が開集合になる
- 任意の x\in X と x_\lambda\to x となる任意のネット(有向点族) (x_\lambda)\subset X に対し, f(x_\lambda)\to f(x) となる
- 任意の x\in X と \mathscr{F}\to x となる X 上の任意のフィルター \mathscr{F} に対し, f(\mathscr{F})\to f(x) となる
3.における定義が,一番ユークリッド空間・距離空間における今までの連続写像の定義に近いと思います。近い点の逆像は近くに(も)あるということです。
3.における冒頭の「任意の」を外して,ある x\in X に対して, f(x) の任意の近傍 N の逆像 f^{-1}(N) が x の近傍になるとき, f は点 x で連続 (continuous) であるといいます。これにより,一般の位相空間でも各点連続が定義できます。
4.は,ちゃんとかけば, f^{-1}(\operatorname{Int}_Y(B))\subset \operatorname{Int}_X(f^{-1}(B)) です。ただし, \operatorname{Int}_X, \operatorname{Int}_Y はそれぞれ X, Y における内部(開核)を表します。
5.は,ちゃんとかけば, f(\overline{A}^X)\subset \overline{f(A)}^Y です。ただし, \overline{\hspace{4pt}\cdot\hspace{4pt}}^X, \overline{\hspace{4pt}\cdot\hspace{4pt}}^Y はそれぞれ X, Y における閉包を表します。
6.は,開集合をすべてチェックしなくても,準開基の逆像が開集合になることさえ調べれば,連続だとわかると言っています。これは有用です。
7.は点列 (x_n) に置き換えてはいけません。それは,点列連続 (sequentially continuous) と言い,連続より弱い概念です(→位相空間における点列連続性と点列連続だが連続でない例)。
さて,定理を証明していきましょう。
1.\iff2.,1.\implies3. \implies5.\implies2.,1.\iff 4.,1.\iff6., 1. \iff 7., 1. \iff 8.の順に示します。 X の部分集合なのか, Y の部分集合なのか気をつけながら読み進めてください。
定理1の証明
1.\iff2.について(開集合のこと \iff 閉集合のこと)
開集合の補集合は閉集合で,閉集合の補集合は開集合であることに注意する。 B\subset Y に対して,
\begin{aligned} f^{-1}(Y\setminus B)& = f^{-1} (Y)\setminus f^{-1}(B) \\&=X\setminus f^{-1}(B)\end{aligned}
であるから, B を開集合や閉集合にすることで,1.\implies2.と2.\implies1.がどちらも示せる。
1.\implies3.について(開集合のこと \implies 近傍のこと)
f(x) の近傍の一つを N\subset Y とすると, f(x)\in O\subset N となる開集合 O\in\mathcal{O}_Y が存在する。このとき,
x\in f^{-1}(O)\subset f^{-1}(N)
である。1.より,f^{-1}(O)\in\mathcal{O}_X なので, f^{-1}(N) は x の近傍である。
3. \implies 5.について(近傍のこと \implies f(\overline{A})\subset \overline{f(A)})
x\in \overline{A} とする。 f(x) の近傍の一つを N\subset Y とすれば,3.より, f^{-1}(N) は x の近傍なので, f^{-1}(N)\cap A \ne \emptyset となる。ゆえに,
\begin{aligned}\emptyset \ne f(f^{-1}(N)\cap A) &\subset f(f^{-1}(N))\cap f(A) \\ &\subset N\cap f(A)\end{aligned}
がわかり, f(A) が f(x) の任意の近傍と共通部分を持つので, f(x)\in \overline{f(A)} である。したがって, f(\overline{A})\subset \overline{f(A)} が示せた。
5. \implies 2.について( f(\overline{A})\subset \overline{f(A)}\implies 閉集合のこと)
F\subset Y を \mathcal{O}_Y-閉集合とすると, A=f^{-1}(F) として5.を適用して,さらに像・逆像の演算規則により,
f(\overline{f^{-1}(F)})\subset \overline{f(f^{-1}(F))}\subset \overline{F}=F
である。両端辺に f^{-1} をつけると, f^{-1}(f(\overline{f^{-1}(F)}))\subset f^{-1}(F) であり,像・逆像の演算規則により \overline{f^{-1}(F)} \subset f^{-1}(f(\overline{f^{-1}(F)})) なので,
となる。これより, f^{-1}(F) は \mathcal{O}_X-閉集合である。
1.\iff4.について(開集合のこと \iff f^{-1}(\operatorname{Int}(B))\subset \operatorname{Int}(f^{-1}(B)))
1. \implies 4.については,1.より, B\subset Y に対し, f^{-1}(\operatorname{Int}(B))\in \mathcal{O}_X であり,かつ f^{-1}(\operatorname{Int}(B))\subset f^{-1}(B) なので分かる。
4. \implies 1.については, B\in\mathcal{O}_Y とすると,4.より f^{-1}(B)\subset \operatorname{Int}(f^{-1}(B)) となるので, f^{-1}(B)\in\mathcal{O}_X であり,1.が言えた。
1.\iff6.について(準開基の逆像が開集合になるだけで必要十分なこと)
準開基の元は開集合なので,1.\implies 6.は明らか。6.\implies 1.について示す。
\mathcal{O}'_Y =\{O\subset Y \mid f^{-1}(O)\in\mathcal{O}_X\}
と定めると,6.より,\mathcal{O}'_Y \supset \mathcal{S}_Y である。像・逆像の演算規則
を用いれば,\mathcal{O}'_Y が位相の定義をみたすことが示せる。したがって, \mathcal{O}'_Y\supset \mathcal{O}( \mathcal{S}_Y) である,ただし右辺は \mathcal{S}_Y により生成される位相のことで, \mathcal{S}_Y は準開基より \mathcal{O}( \mathcal{S}_Y)=\mathcal{O}_Y である。よって,題意は示された。
1.\iff7.については,ネット(有向点族)による位相空間論と点列との比較内で証明している。
1.\iff8.については,位相空間におけるフィルターの概念を詳しく内で証明している。
証明終
6.と, \{(-\infty, a), (b, \infty)\mid a,b\in\R\} が \R の準開基になることより,実数値関数 f\colon X\to \R が連続であることを確認するには, a,b\in\R に対し,
\{ x\in X\mid f(x)<a\} ,\quad\{ x\in X\mid f(x)>b\}
が開集合になるかどうかのみを確認すればよい,ということが分かります。
連続写像の例
一般の連続写像の例をいくつか述べましょう。以下で, (X,\mathcal{O}_X), (Y,\mathcal{O}_Y) は空でない位相空間とします。例2.から始まりますが,例1.は定理1.の前にやりました。
連続写像の例2(定数関数).
f\colon X\to Y が任意の x\in X に対して f(x)\in Y が常に同じ値となるとき, f は連続である。
f(x)=c\in Y \: (x\in X) とすると, O\in\mathcal{O}_Y について,
f^{-1}(O) = \begin{cases} X & c\in O, \\ \emptyset & c\in X\setminus O\end{cases}
が成り立ち,いずれにせよ f^{-1}(O)\in\mathcal{O}_X ですから,連続ですね。タイトルは「定数関数」としましたが,「定値写像」と言った方が正しいと思います。
f^{-1}(\emptyset)=\emptyset\in\mathcal{O}_X と f^{-1}(Y)=X\in\mathcal{O}_X より,連続です。
密着空間は全ての点が「密着」しているので,そこに値を持つ写像は「ひとつながり」に値を持つと考えられるわけです。
任意の B\subset Y に対し, f^{-1}(B)\in 2^X ですから,連続です。
離散空間は全ての点が「離れて」いるので,定義域が飛び飛びの写像と考えられ,どんな写像だろうと連続と言わざるを得ないわけです。
連続写像の例5(恒等写像).
\mathcal{O}_1, \mathcal{O}_2 を X 上の位相とする。
恒等写像 \mathrm{id}\colon (X,\mathcal{O}_1)\to (X,\mathcal{O}_2) が連続となる必要十分条件は,\mathcal{O}_1\supset \mathcal{O}_2 が成り立つことである。
恒等写像とは,\mathrm{id}(x)=x となる写像です。 A\subset X に対し,\mathrm{id}^{-1}(A)=A ですから,明らかでしょう。定義域の位相の方が細かい(大きい・強い)ということです。
連続写像の例6(包含写像).
X\subset Y とする。包含写像 \iota\colon X\to Y が連続となる必要十分条件は,
\mathcal{O}_X\supset \{ O_Y\cap A\mid O_Y\in\mathcal{O}_Y\}
が成り立つことである。
包含写像も \iota(x)=x であることに変わりありません。定義域の位相が, \mathcal{O}_Y によって定まる X の相対位相より細かい(大きい・強い)ということです。これは, B\subset Y に対し,\iota^{-1}(B)=B\cap X となることからわかります。
連続写像の例7.
f\colon (X,\mathcal{O}_X) \to (Y,\mathcal{O}_Y) が連続であるとき,開集合系を \mathcal{O}'_X\supset \mathcal{O}_X, \, \mathcal{O}'_Y\subset \mathcal{O}_Y に入れ替えた写像 f\colon (X,\mathcal{O}'_X) \to (Y,\mathcal{O}'_Y) も連続である。
これはすなわち,定義域の位相は大きければ大きいほど(細かければ細かいほど),終域の位相は小さければ小さいほど(粗ければ粗いほど)連続になりやすいということです。
ユークリッド空間・距離空間との連続写像の定義の一貫性
位相空間における連続写像の定義は,ユークリッド空間や距離空間における連続写像の定義の一般化になっています。これを説明しておきましょう。
ユークリッド空間における f \colon \R\to \R が連続写像となる定義 \lim_{x\to a}f(x)=f(a) を用いて,一貫性を説明しましょう。まずは,イプシロンデルタ論法と呼ばれる定義を復習します。
関数 f\colon \R\to \R が点 x\in \R で連続 (continuous) であるとは,任意の \varepsilon >0 に対し,ある \delta>0 が存在して,
\large \color{red} |y-x|<\delta \implies |f(y)-f(x)|<\varepsilon
とできることである。これを, \lim_{y\to x}f(y)=f(x) とかく。
これと,一般の位相空間における連続性の定義の一貫性を確認しましょう。イプシロンデルタ論法の根幹の部分である |y-x|<\delta \implies |f(y)-f(x)|<\varepsilon の部分は,逆像の言葉でかくことができます。
実際, |y-x|<\delta とは, y\in (x-\delta, x+\delta) とかけます。 |f(y)-f(x)|<\varepsilon とは, f(y)\in (f(x)-\varepsilon , f(x)+\varepsilon) とかけます。また, f(a)\in B とは a\in f^{-1}(B) ともかけるので, a\in A\implies f(a) \in B というのは, A\subset f^{-1}(B) とかいても同じことです。
これを踏まえると, |y-x|<\delta \implies |f(y)-f(x)|<\varepsilon の部分は,
\color{red} (x-\delta, x+\delta)\subset f^{-1}\bigl((f(x)-\varepsilon, f(x)+\varepsilon)\bigr)
とかけます。「任意の \varepsilon >0 に対し,ある \delta>0 が存在して,」なので,任意の f(x) の近傍 (f(x)-\varepsilon, f(x)+\varepsilon) に対し,その逆像 f^{-1}\bigl((f(x)-\varepsilon, f(x)+\varepsilon)\bigr) は, x のある近傍 (x-\delta, x+\delta) を含んでいる,といえます。 x の近傍を含んでいるような集合は,それ自身が近傍ですから,さらに言い換えると,
任意の f(x) の近傍に対し,その逆像は x の近傍になる
と言ってもいいです。これは,定理1.3でやった,「近傍の逆像」による連続写像の定義と同じですね。
以上から,位相空間における連続写像の定義と,イプシロンデルタ論法による連続写像の定義が一貫していることが確認できました。
連続写像の性質と連続写像によって保たれる性質・保たれない性質
ここからは,連続写像自体が持つ性質と,連続写像によって保たれる位相的性質を紹介します。
連続写像の性質
定理2(連続写像の合成)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y), (Z, \mathcal{O}_Z) を位相空間とし, f\colon X\to Y, \, g\colon Y\to Z とする。
f,g が連続であるとき,その合成 g\circ f\colon X\to Z も連続である。
証明
(g\circ f)^{-1} = f^{-1}\circ g^{-1} に注意する。 O\in\mathcal{O}_Z とする。 g は連続より,g^{-1}(O)\in\mathcal{O}_Y である。これと, f が連続であることより, f^{-1}(g^{-1}(O))\in\mathcal{O}_X である。したがって示された。
証明終
定理3(連続写像の制限)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y を連続とする。
A\subset X を空でない集合とし, (A, \mathcal{O}_A) を, X から定まる相対位相とすると, f の A の制限 f|_A\colon A\to Y も連続となる。
f(X)\subset Y に, Y から定まる相対位相を入れると,終域を f(X)\subset Y に制限した写像 f\colon X\to f(X) も連続である
証明
前半について
O\in \mathcal{O}_Y とすると,{ f|_A}^{-1}(O)=f^{-1}(O)\cap A\in\mathcal{O}_A より,わかる。
後半について
部分空間 f(X)\subset Y における開集合は V\in\mathcal{O}_Y を用いて V\cap f(X) とかける。これは,
\begin{aligned} f^{-1} (V\cap f(X)) &= f^{-1}(V) \cap f^{-1}(f(X))\\&= f^{-1}(V)\cap X\\&= f^{-1}(V) \in\mathcal{O}_X\end{aligned}
となるため, f\colon X\to f(X) は連続である。
証明終
連続写像によって保たれる性質・保たれない性質
ここからは,連続写像によって保たれる位相的性質・保たれない性質を紹介します。
定理4(連続写像によって保たれる性質)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y は連続とする。このとき,
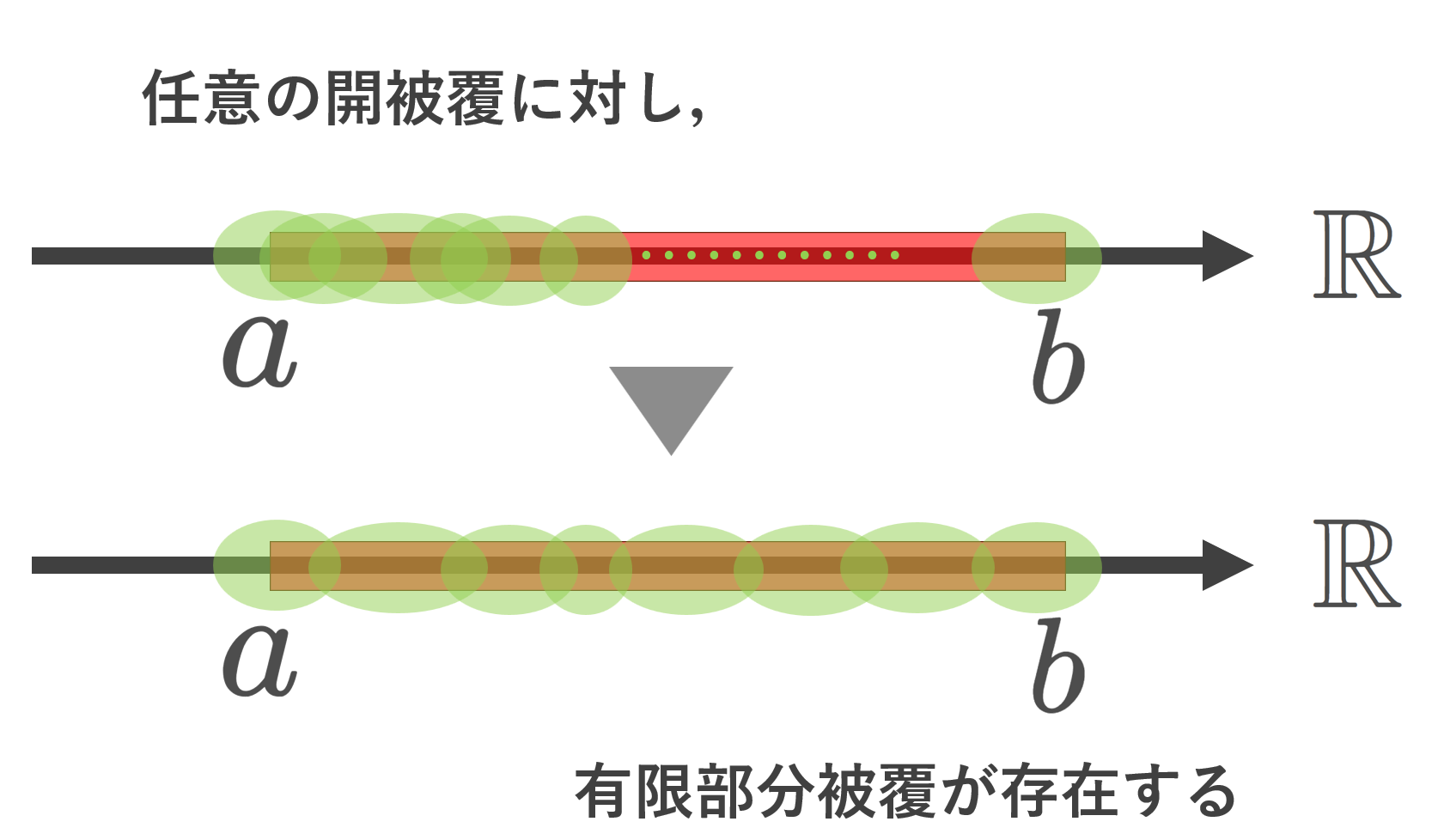
1.の証明は,コンパクト空間とコンパクト集合について詳しくにあります。2.は【位相空間】リンデレーフ空間の定義・性質・具体例に同じ定理をかきましたが,証明は1.と同じです。3.の証明は,位相空間における連結性について詳しくにあります。4.の証明は弧状連結・弧連結について定義・具体例・性質にあります。5.の証明は,【位相空間】稠密性と可分性~定義と具体例11個~にあります。
次は,「定理」というのは不適切かもしれませんが,保たれない性質も紹介しておきましょう。
定理5(連続写像によって保たれない性質)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y は連続とする。このとき,
分離公理は,基本的に性質を保ちません。分かりやすい反例は,離散位相 (X, 2^X) から密着位相 (X, \{\emptyset, X\}) への恒等写像です。
コンパクト性や連結性のように,位相が粗い(小さい・弱い)ほどありがたい概念は,連続写像によって保たれることが多いです。逆に分離公理のように,位相が細かい(大きい・強い)ほどありがたい概念は,連続写像によって保たれることは少ないです。
定理6(連続写像によって保たれない性質)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y は連続とする。このとき,
たとえば,実数全体の集合 \R に対し,\mathcal{O}_{\mathrm{cof}} を補有限位相 (cofinite topology) ,すなわち,
\mathcal{O}_{\mathrm{cof}}=\{A\subset \R \mid \R \setminus A\text{ is finite}\}
のように,補集合が有限集合である位相とします。このとき, (\R,\mathcal{O}_\mathrm{cof}) は第一可算ではありません(→補有限位相と補可算位相について掘り下げる)。したがって,第二可算でもありません。ここで,通常のユークリッド空間による位相 (\R, \mathcal{O}) からの恒等写像 \mathrm{id}\colon (\R, \mathcal{O})\to (\R,\mathcal{O}_\mathrm{cof}) を考えます。この恒等写像は, \mathcal{O}\supset \mathcal{O}_{\mathrm{cof}} より連続であり, (\R, \mathcal{O}) は第一可算かつ第二可算なので,1, 2.の反例になっています。
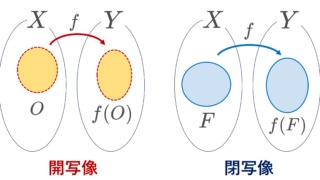
ただし, f が開写像であることを追加で課すと,近傍の像が近傍になるため,正しいことが証明できます。
関連する記事
位相空間とは関係ありませんが,連続性に関係する記事を挙げましょう。