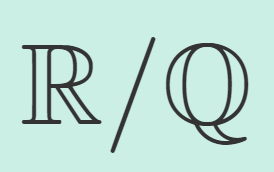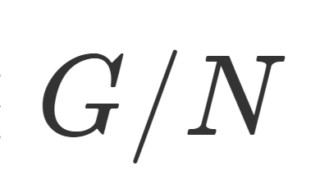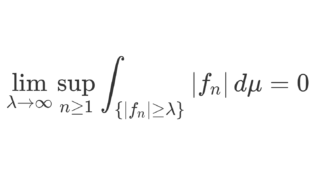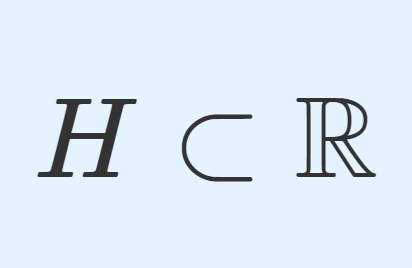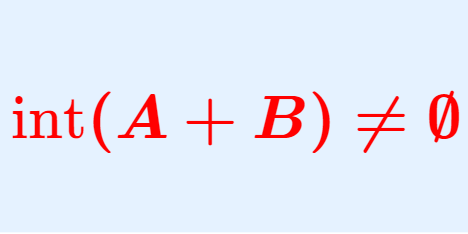ヴィタリ集合とは,剰余群 \R/\mathbb{Q} における各代表元の集合を指し,選択公理を仮定することで存在が認められます。ヴィタリ集合はルベーグ非可測集合の例として有名です。
ヴィタリ集合について,その構成とルベーグ非可測であることの証明を行いましょう。
ヴィタリ集合とは
本記事では群論の基礎を仮定し,簡潔に述べることにしましょう。
定義(ヴィタリ集合)
剰余群(商群) \R/\mathbb{Q} について,各剰余類の代表元を [0,1) の元として取ることで, \R/\mathbb{Q}\subset [0,1) とみなす。これは選択公理より可能である。
このときの V=\R/\mathbb{Q} \subset [0,1) をヴィタリ集合 (Vitali set) という。
\R/\mathbb{Q} の各元は
r+\mathbb{Q} = \{ r+q\mid q\in\mathbb{Q}\}
という形をしており,これを \R における \mathbb{Q} の剰余類 (residue class) といいます。このときの r を剰余類 r+\mathbb{Q} の代表元といい,
ですから,代表元の取り方は無数にあります。各剰余類に対し,その代表元を r\in [0,1) になるように取ったとしましょう(ここで選択公理を用います)。代表元の集合を V\subset [0,1) とすると,
であり, V の各元 v,v'\in V,\; v\ne v' はそれぞれ異なる剰余類の代表元 ( v+\mathbb{Q}\ne v'+\mathbb{Q} ) ですから,v-v'\notin \mathbb{Q} が成り立ちます。各剰余類は \R を「同値類で分割」するということでしたから,
です(右辺は集合の非交和を意味します)。また,これを変形して,
が成り立ちます。和の交換をしていますが,集合の和集合を考えているだけなので,問題ありません。
なお,(選択公理を認めると)代表元の選び方は一通りではないので,ヴィタリ集合 V は一意に定まる集合ではありません。
ヴィタリ集合はルベーグ非可測集合
次は非常に有名です。
定理(ヴィタリ集合はルベーグ非可測)
ヴィタリ集合 V\subset [0,1) はルベーグ非可測集合である。
背理法で証明します。 [0,1) を \mathbb{R}/\mathbb{Z} と同一視することで,証明が明快になります。
証明
V\subset [0,1)=\R/\mathbb{Z} をルベーグ可測とする。このとき, (4) 式を考えると,
[0,1)= \sum_{q\in \mathbb{Q}\cap [0,1)} (V+q)\quad\text{in } \R/\mathbb{Z}
である(右辺は非交和)。\mu をルベーグ測度とすると,測度の可算加法性より,
ルベーグ測度の平行移動不変性より,任意の q\in \mathbb{Q}\cap [0,1) に対して, \mu(V+q)=\mu(V) \text { in } [0,1)= \mathbb{R}/\mathbb{Z} である。 (5) 式より,
\mu(V)=0 とすると, (6) 式は 1=0 となって矛盾し, \mu(V)>0 とすると, 1=\infty となって矛盾する。よって, V はルベーグ可測でない。
証明終
群論が分かっていないと, \R/\mathbb{Z} 上で考えているというのが分からないかもしれません。 \R/\mathbb{Q}=(\R/\mathbb{Z})/(\mathbb{Q}/\mathbb{Z}) から,最初から {}\bmod \mathbb{Z} で考えていると思うのが,しっくりくるでしょう。
なお,今回は選択公理を仮定しましたが,選択公理なしでは,ルベーグ非可測集合が作れないことも知られているようです。