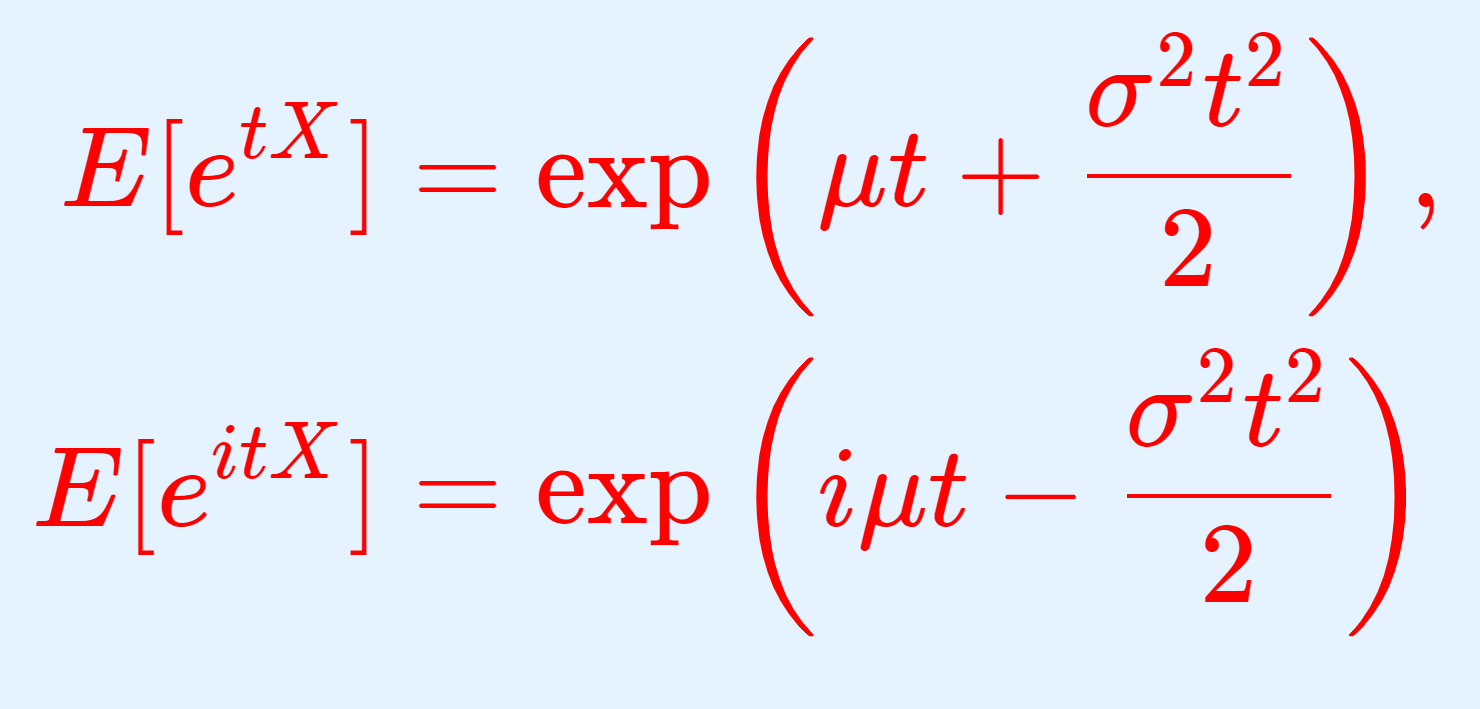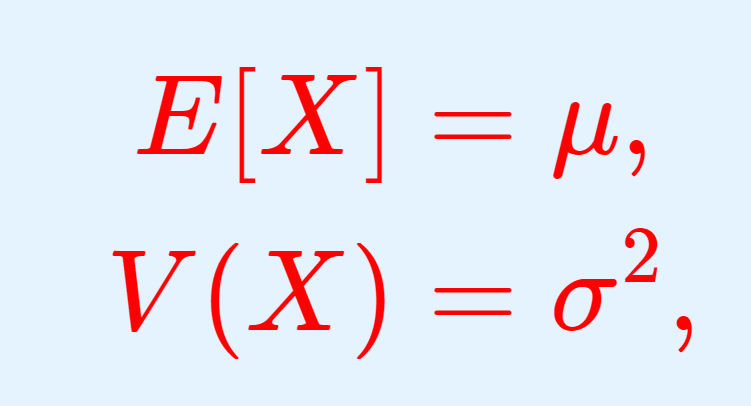正規分布の積率母関数(モーメント母関数)・特性関数は,それぞれ
\begin{aligned} E[e^{tX}]&= \exp \left( \mu t + \frac{\sigma^2 t^2}{2} \right) , \\ E[e^{itX}]&= \exp \left( i\mu t - \frac{\sigma^2 t^2}{2} \right) \\ \end{aligned}
となります。これについて,その導出の証明を行いましょう。
正規分布の積率母関数(モーメント母関数)・特性関数
まずは,ちゃんと定理の主張を述べましょう。
定理(正規分布の積率母関数(モーメント母関数)・特性関数)
X\sim N(\mu,\sigma^2 ) とする。このとき, X の積率母関数(モーメント母関数)・特性関数はそれぞれ t\in\mathbb{R} とすると,
\color{red} \begin{aligned} E[e^{tX}]&= \exp \left( \mu t + \frac{\sigma^2 t^2}{2} \right) , \\ E[e^{itX}]&= \exp \left( i\mu t - \frac{\sigma^2 t^2}{2} \right) \\ \end{aligned}
である。
以上が今回のテーマです。導出の証明に入る前に,まずは正規分布の定義を確認しておきましょう。
X を確率変数, \mu\in \mathbb{R},\; \sigma > 0 とする。 X の確率密度関数が
\color{red} p(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
となるとき, X は平均 \mu ,分散 \sigma^2 の正規分布 (normal distribution) に従うといい, \color{red} X\sim N(\mu, \sigma^2) とかく。
正規分布のまとめについては,以下の記事を参考にしてください。
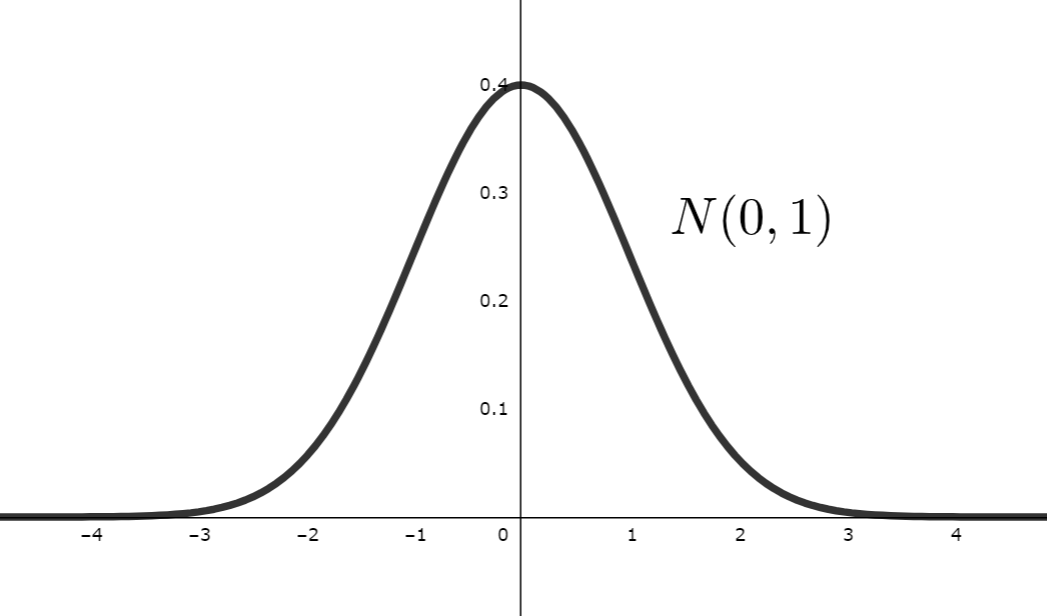
また, \mu=0 , \;\sigma=1 となる N(0,1) を標準正規分布 (standard normal distribution) といいます。このときの積率母関数(モーメント母関数)・特性関数は,
\begin{aligned} E[e^{tX}]&= e^{t^2/2}, \\ E[e^{itX}]&= e^{ - t^2/2 } \\ \end{aligned}
となります。
正規分布の積率母関数(モーメント母関数)・特性関数の導出証明
さて,早速導出していきましょう。
正規分布の積率母関数(モーメント母関数)の導出
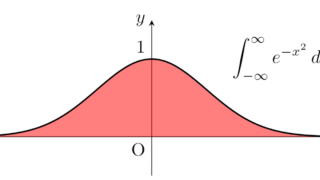
導出にはガウス積分の知識が必要です。これは
\int_{0}^\infty e^{-x^2}\, dx = \frac{\sqrt{\pi}}{2}
という積分のことを指します。これについては,以下で解説しています。
これを前提として,証明していきましょう。
証明
積率母関数(モーメント母関数)の定義と,正規分布の確率密度関数を考慮して,
\begin{aligned} E[e^{tX}] &= \int_{-\infty}^\infty e^{tx} p(x)\, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty e^{tx} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty e^{-\frac{(x-\mu)^2}{2\sigma^2}+tx}\, dx \end{aligned}
となる。ここで,指数部分について,
であるから,
ここで,置換積分・ガウス積分により,
である。特に,最後の等式は, N(0,\sigma^2) の正規分布の確率密度関数と等しいことからも分かることに注意する。結局,
となる。よって, E[e^{tX}] = e^{\mu t+\frac{\sigma^2t^2}{2}}.
証明終
無事に導出できましたね。
正規分布の特性関数の導出
特性関数の導出は,積率母関数(モーメント母関数)の導出に似ていますが,ガウス積分の部分に,複素数が出てくるので注意が必要です。確認していきましょう。
証明
特性関数の定義と,正規分布の確率密度関数を考慮して,
\begin{aligned} E[e^{itX}] &= \int_{-\infty}^\infty e^{itx} p(x)\, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty e^{itx} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty e^{-\frac{(x-\mu)^2}{2\sigma^2}+itx}\, dx \end{aligned}
となる。ここで,指数部分について,
であるから,
ここで,複素数に拡張したガウス積分(後述)により,
であるから,結局,
となる。よって, E[e^{tX}] = e^{i\mu t-\frac{\sigma^2t^2}{2}}.
証明終
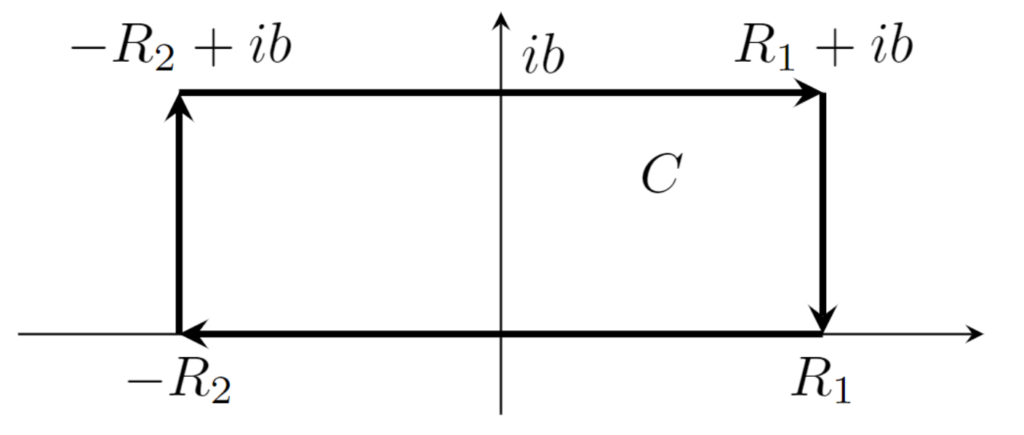
複素数に拡張したガウス積分の部分は,置換積分すればスグに求まるわけではありません。なぜなら,置換積分すると,
\begin{aligned} &\frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^\infty e^{-\frac{\{x-(\mu+i\sigma^2 t)\}^2}{2\sigma^2}}\, dx\\ &= \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty-i\sigma^2t}^{+\infty-i\sigma^2t} e^{-\frac{y^2}{2\sigma^2}}\, dx\end{aligned}
となって,結局,積分区間に複素数が残ってしまうからです。じゃあどうするかというと,複素関数論の知識を用いて,以下のような経路積分を行い, R_1,R_2\to\infty とします。
詳しいことは,以下で解説しています。