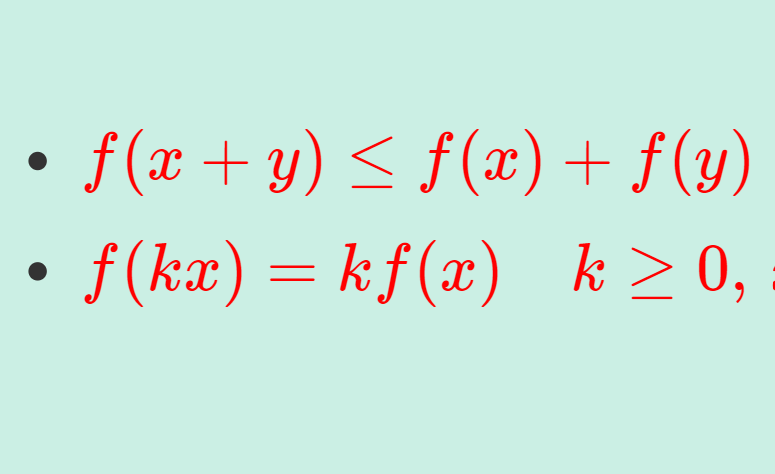授業やセミナーといった「ラフ」な場面でよく用いられる,数学英語における共通の「略語」を紹介します。
なお,自身の身の回りのものを反映しているため,人によって流儀が違う可能性があります。変なものがありましたらお知らせください。
アルファベット順です。
| 略語 | 正式名称 | 意味 | 使用例 |
|---|---|---|---|
| abs., absol. | absolute(ly) | 絶対に | f is abs. conti. w.r.t. Lebesgue meas. (ルベーグ測度に関して絶対連続) |
| a.e. | almost everywhere | (測度論において)ほとんどいたるところ | f(x) = 0, \,\,\text{a.e. } x \in \mathbb{R}. |
| a.s. | almost surely | (確率論において)確率1で | X > 0, \,\, \mathbb{P}\text{-a.s.} |
| bdd. | bounded | 有界 | Let f : bdd. conti. (有界連続) |
| cf. | confer (ラテン語) | 参照せよ,比較せよ | cf. [3]. (3番の文献を参照せよ) |
| clopen | closed-open set | 開かつ閉集合 | |
| Conj. | Conjecture | 予想 | Conj.6.3. |
| const. | constant | 定数 | Let C >0 : const. |
| conti. | continuous | 連続 | |
| conv. | convergence | 収束 | L^1 conv. ( L^1 収束) |
| Cor. | Corollary | 系 | Cor.3.6. |
| cpt. | compact | コンパクト | |
| Def. | Definition | 定義 | Def.2.1. |
| dim. | dimension | 次元 | \dim V |
| e.g. | exempli gratia (ラテン語) | たとえば, for example | See, e.g., [2]. (文献2番を見よ) |
| etc. | et cetera (ラテン語) | 等々, and so on | |
| et al. | et alia (ラテン語) | その他の人, and others | See [Chen et al., 2016]. (筆頭著者のChenさんとその他の人が書いた2016年の文献をみよ) |
| eq. | equation, equality | 等式 | eq. (2.17) ((2.17)の等式) |
| Ex. | Exercise | 演習(問題) | Ex.2.8. |
| exp. | exponential | 指数, e の何乗 | \exp(x) = e^x |
| func., fun., fn. | function | 関数 | |
| G.C.D. | greatest common divisor | 最大公約数 | |
| hom., homo. | homomorphism | 準同型写像 | |
| homeo. | homeomorphism | 同相写像 | |
| i.e. | id est (ラテン語) | すなわち | ~, i.e., ~ |
| iff | if and only if | 同値,必要十分条件 | |
| inf. | infimum | 下限 | \inf_{x>0} f(x) |
| L.C.M. | least common multiple | 最小公倍数 | |
| Lem. | Lemma | 補題 | Lem.3.1. |
| LHS | left hand side | (数式における)左辺 | LHS of (3.16) = ~ ((3.16)式の左辺は以下のように変形できる) |
| loc. | local(ly) | 局所的に | loc. bdd. (局所的に有界) |
| max. | maximum | 最大値 | \max_{0 \le x \le 1} f(x) |
| meas. | measure | 測度 | Lebesgue meas. (ルベーグ測度) |
| mfd. | manifold | 多様体 | |
| min. | minimum | 最小値 | \min_{0 \le x \le 1} f(x) |
| nbd., nbhd. | neighborhood | 近傍 | nbd. of x |
| ONB, CONS | orthonormal basis, complete orthonormal system | 正規直交基底, 完全正規直交系 | |
| ONS | orthonormal system | 正規直交系 | |
| pf., prf. | proof | 証明 | |
| prod. | product | 積 | |
| pt. | point | 点 | |
| Prop. | Proposition | 命題 | Prop.3.4. |
| Q.E.D. | quod erat demonstrandum (ラテン語) | 証明終わり | |
| Rem. | Remark | 注意 | Rem.5.1. |
| RHS | right hand side | (数式における)右辺 | RHS of (3.16) = ~ ((3.16)式の右辺は以下のように変形できる) |
| resp. | respectively | それぞれ | |
| r.v. | random variable | 確率変数 | Let X: r.v. |
| seq. | sequence | 列(数列,関数列など) | \{ f_n \} : seq. of func. (関数列) |
| sp. | space | 空間 | vec. sp. (ベクトル空間) |
| s.t. | such that ~ | ~が成立する | There exists c>0 s.t. ~ |
| sup. | supremum | 上限 | \sup_{x>0} f(x) |
| supp. | support | (関数の)台 | f has cpt. supp. (台がコンパクトな関数) |
| sym. | symmetric | 対称の | |
| TBA | to be announced | 後ほど告知する | 講演タイトル:TBA |
| TFAE | The following are equivalent | 以下は全て同値である | TFAE: (i) ~, (ii) ~ , (iii) ~. |
| Th., Thm. | Theorem | 定理 | Th.5.6. |
| top. | topological | 位相 | top. sp. (位相空間) |
| unif., uni. | uniform(ly) | 一様に | f is unif. conti.(一様連続) |
| Var. | variance | 分散(確率) | \operatorname{Var}(X) |
| vec., vect. | vector | ベクトル | vec. sp. (ベクトル空間) |
| viz. | videlicet (ラテン語) | すなわち | |
| WLOG | without loss of generality | 一般性を失わずに | |
| w.r.t. | with respect to | ~に関して | f_m(x) is bdd. w.r.t. x (xについて有界) |
随時追記します。