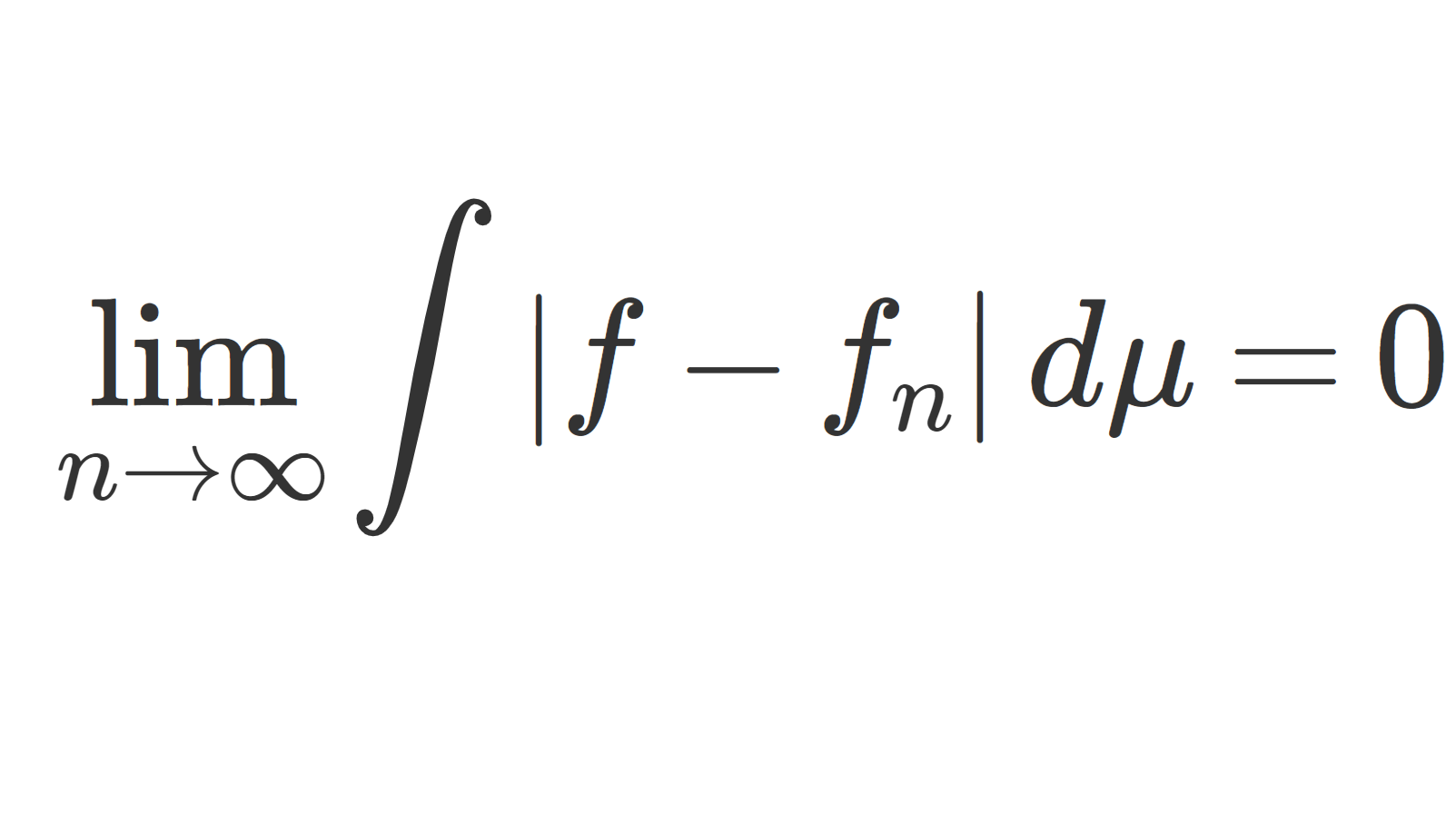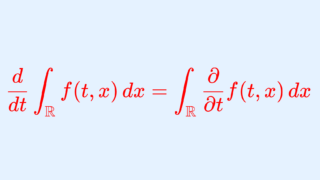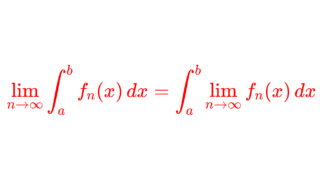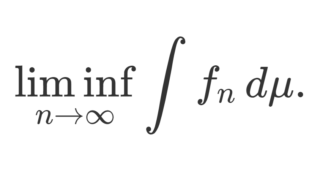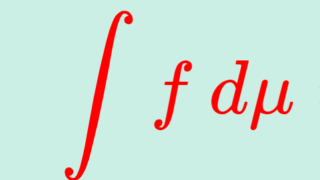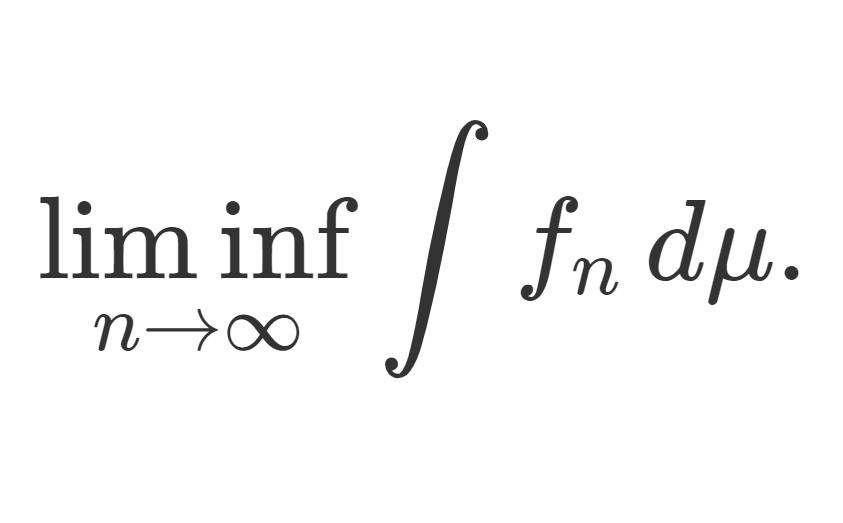ルベーグの収束定理 (優収束定理; dominated convergence theorem, DCT) とは,ルベーグ積分・測度論における「積分と極限の交換定理」の1つで,ルベーグ積分の根幹をなす定理といえます。
ルベーグの収束定理について,その主張と例題・証明を行っていきましょう。
ルベーグの収束定理(優収束定理)
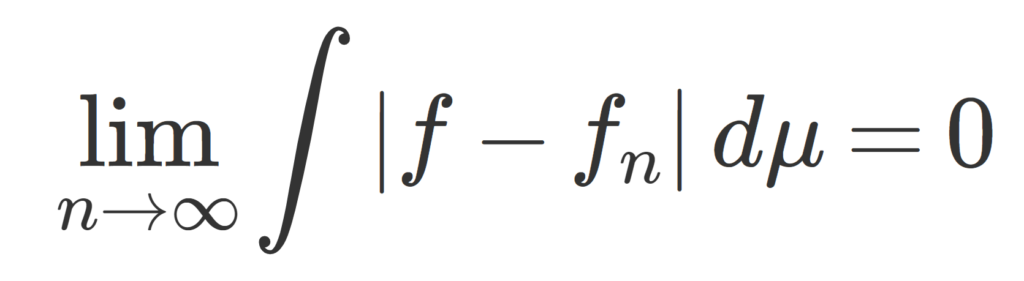
ルベーグの収束定理(優収束定理)
定理1(ルベーグの収束定理)
(X,\mathcal{F},\mu) を測度空間, \{f_n\} をその上の可測関数列とし,以下の2つの条件
- f_n \xrightarrow{n\to\infty} f
- |f_n|\le F \; (n\ge 1) となる可積分関数 F が存在する
の両方が成立するとき, f_n, f は可積分で
\color{red}\lim_{n\to\infty} \int |f_n-f|\,d\mu = 0
が成り立つ。特に,
である。(このときの F を優関数 (dominating function) と呼ぶ)
ここで f が可積分 (integrable) とは, \int |f|\,d\mu<\infty が成り立つことでした。
後半の等式を書き換えると,
\color{red}\lim_{n\to\infty} \int f_n\,d\mu =\int \lim_{n\to\infty}f_n\,d\mu
ですから,積分と極限の交換定理ですね。ルベーグ積分はリーマン積分に比べて,積分と極限の交換が行いやすいというメリットがあり,その根幹をなすのがこの定理です。単調収束定理・Fatouの補題と並び,ルベーグ積分における最も大事な定理と言っても良いでしょう。
なお, f_n \xrightarrow{n\to\infty} f や |f_n|\le F \; (n\ge 1) の部分は,各点ではなく \mu\text{-a.e.} でも構いません。零集合( \mu(N)=0 となる集合 N)上の関数の値は積分に影響しないからです。
なお,可積分優関数 F の存在を仮定しないと反例があります。実際, f_n=1_{[n,n+1]} とすると,
\begin{gathered}\lim_{n\to\infty} \int 1_{[n,n+1]}\,d\mu =1,\\ \int \lim_{n\to\infty} 1_{[n,n+1]}\, d\mu = \int 0\,d\mu = 0 \end{gathered}
となって,値が一致していませんね。
有界収束定理
特に,有限測度空間 \mu(X)<\infty のときは,有界収束定理と呼ばれる以下の定理が成立します。「ルベーグの収束定理」の特別なバージョンです。
定理2(有界収束定理)
(X,\mathcal{F},\mu) を \color{red} \mu(X)<\infty をみたす測度空間, \{f_n\} をその上の可測関数列とし,以下の2つの条件
- f_n \xrightarrow{n\to\infty} f
- |f_n|\le M\; (n\ge 1) となる定数 M が存在する( n によらず一様に有界)
の両方が成立するとき, f_n, f は可積分で
\color{red}\lim_{n\to\infty} \int |f_n-f|\,d\mu = 0
が成り立つ。特に,
である。
これの証明はルベーグの収束定理を認めれば簡単です。 \mu(X)<\infty なら定数関数 M \ge 0 は \int M\,d\mu = M\mu(X)<\infty で可積分ですから, M が可積分優関数となるからです。
ルベーグの収束定理(優収束定理)の例題
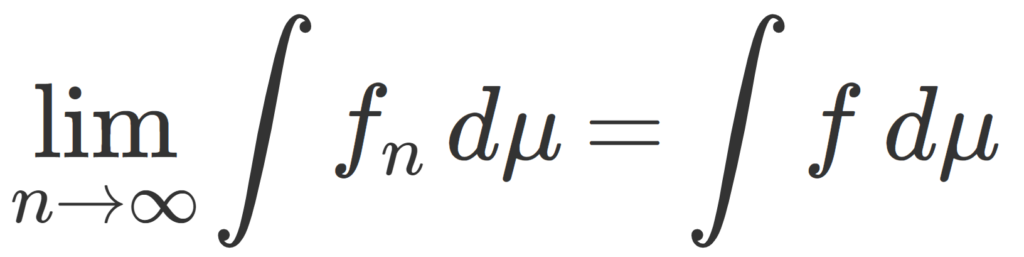
例題1.
\displaystyle \lim_{n\to\infty} \int_0^\infty \frac{1}{1+x^n}\, dx を求めよ。
n\ge 2 に対し, \left|\dfrac{1}{1+x^n}\right| \le \min\left\{1, \dfrac{1}{x^2} \right\} であり,右辺は n によらずかつ (0,\infty) 上可積分ですから,ルベーグの収束定理より
\begin{aligned} \lim_{n\to\infty} \int_0^\infty \frac{1}{1+x^n}\, dx &= \int_0^\infty\lim_{n\to\infty} \frac{1}{1+x^n}\, dx \\ &= \int_0^\infty \left(1_{[0,1)}+ \frac{1_{\{1\}}}{2} \right)\, dx \\&= 1 \end{aligned}
となりますね。優関数は n によらずに取らねばならないことに注意してください。たとえば,答案に \left|\dfrac{1}{1+x^n}\right| \le \min\left\{1, \dfrac{1}{x^n} \right\} と書いてしまうと減点されるでしょう。初学者はココを間違いがちです。
例題2.
\displaystyle\lim_{n\to\infty} \int_0^{\pi/2} \sin^n \theta \,d\theta を求めよ。
|\sin^n\theta|\le 1 かつ \sin^n \theta \xrightarrow{n\to\infty} 0,\; \text{a.e.} より,有界収束定理から
\lim_{n\to\infty} \int_0^{\pi/2} \sin^n \theta \,d\theta = \int_0^{\pi/2} 0 \,d\theta = 0
ですね。なお, \int_0^{\pi/2} \sin^n \theta \,d\theta 自体を計算したい場合は【ウォリス積分】sin,cosのn乗積分の導出と性質で解説しています。
もう一問やってみましょう。以下で,優関数は t に依存せず取らねばならないことに注意してください。
例題3.
\displaystyle \lim_{t\to\infty} \int_1^\infty tx e^{-tx^3} \,dx を求めよ。
f(t)= tx e^{-tx^3} とおくと, f'(t)= (x-tx^4) e^{-tx^3} から関数の増減を考えることで, |f(t)|\le 1/x^2 がわかります。右辺は (1,\infty) 上可積分より,ルベーグの収束定理が使えて, \lim_{t\to\infty} \int_1^\infty tx e^{-tx^3} \,dx = \int_1^\infty \lim_{t\to\infty}tx e^{-tx^3} \,dx=0
が求まります。
ここで,ルベーグの収束定理は「列の極限の定理」より,本来は点列 \{t_n\} を t_n\xrightarrow{n\to\infty} \infty となるように取って適用せねばなりません。しかし,どんな点列をとっても積分の極限は 0 になりますから,結局 t\to\infty で考えてもいい訳です(→実数上関数の収束と数列の収束の同値性とその証明)。
ルベーグの収束定理(優収束定理)の証明
定理を再掲しましょう。
定理1再掲(ルベーグの収束定理)
(X,\mathcal{F},\mu) を測度空間, \{f_n\} をその上の可測関数列とし,以下の2つの条件
- f_n \xrightarrow{n\to\infty} f
- |f_n|\le F \; (n\ge 1) となる可積分関数 F が存在する
の両方が成立するとき, f_n, f は可積分で
\lim_{n\to\infty} \int |f_n-f|\,d\mu = 0
が成り立つ。特に,
である。(このときの F を優関数 (dominating function) と呼ぶ)
ルベーグの収束定理の証明には,Fatouの補題を用います。
\{f_n\} を非負可測関数の列とする。このとき,
\int \liminf_{n\to\infty} f_n\,d\mu\le \liminf_{n\to\infty} \int f_n\,d\mu.これの証明はFatouの補題とその証明・具体例・活用例で行っています。これを認めて証明しましょう。
証明
|f_n|\le F と n\to\infty として |f|\le F より, f_n, f の可積分性は明らか。
|f_n-f| \le |f_n|+|f|\le 2F より, 2F-|f_n-f|\ge 0 であるから,Fatouの補題より,
\begin{aligned}\int 2F\,d\mu &=\int \liminf_{n\to\infty} (2F-|f_n-f|)\,d\mu\\ &\le \liminf_{n\to\infty}\int (2F- |f_n-f|)\,d\mu.\end{aligned}
両端辺 \int 2F\,d\mu を引くと,0\le \liminf_{n\to\infty}\int - |f_n-f| \,d\mu ,すなわち
よって \lim_{n\to\infty}\int |f_n-f| \,d\mu=0 を得る。特に,
より,後半の等式も従う。
証明終
微分と積分の交換定理
ルベーグの収束定理を用いることで,直ちに微分と積分の交換定理が導けます。詳しくは以下で解説しています。