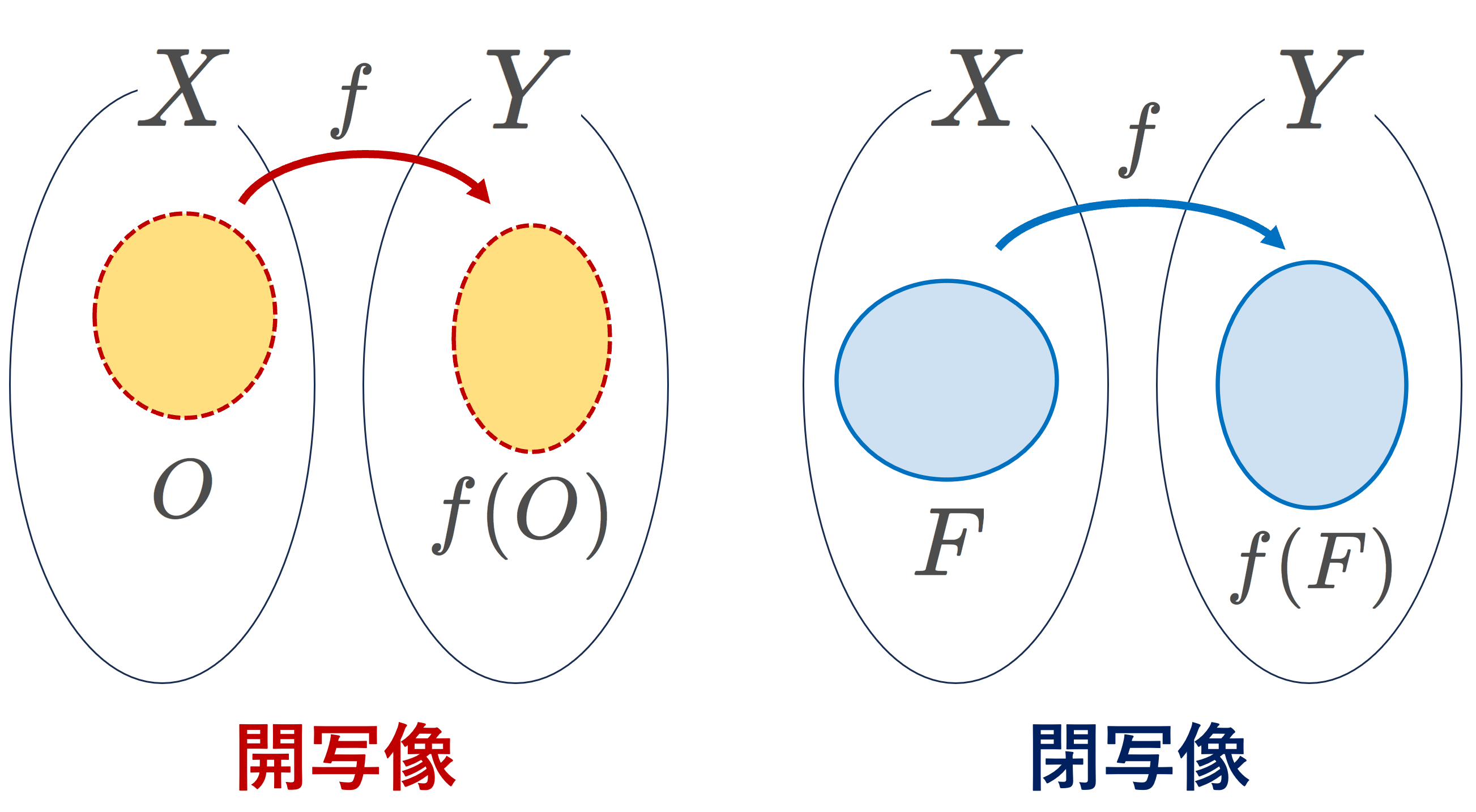
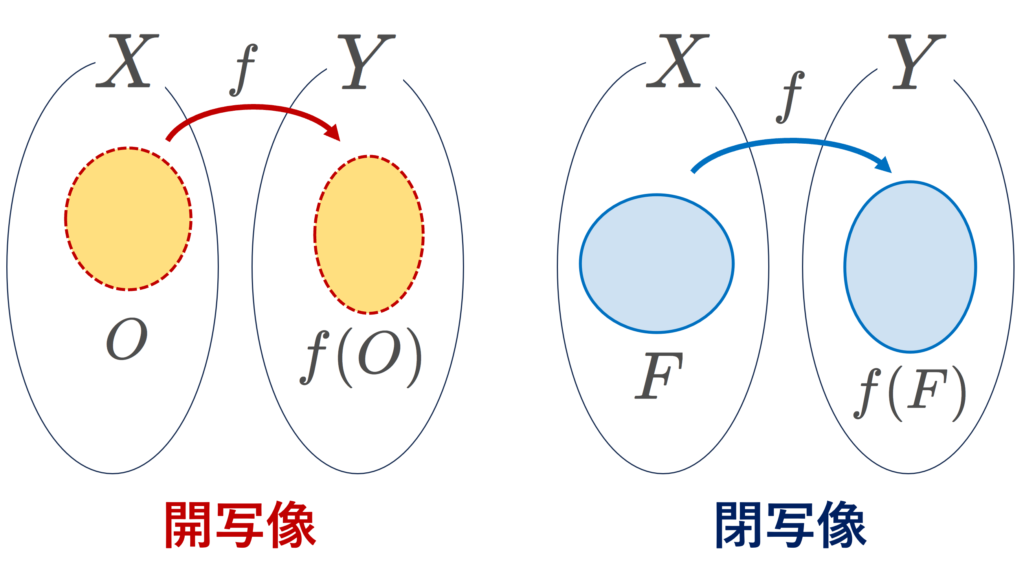
開写像とは,開集合の像(image)を開集合にうつす写像のことで,閉写像とは,閉集合の像(image)を閉集合にうつす写像のことです。
開集合・閉写像の定義と具体例・性質を,連続写像と絡めながら解説しましょう。
開写像・閉写像の定義
定義(開写像・閉写像)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし,\mathcal{F}_X, \mathcal{F}_Y をそれぞれ X, Y の閉集合族とする。さらに, f\colon X\to Y とする。
- \color{red} O_X\in \mathcal{O}_X\implies f(O_X)\in\mathcal{O}_Y が成り立つとき, f を開写像 (open map) という。
- \color{red}F_X\in \mathcal{F}_X\implies f(F_X)\in\mathcal{F}_Y が成り立つとき, f を閉写像 (closed map) という。
開集合の像が開集合となるものが開写像,閉集合の像が閉集合となるものが閉写像です。開写像と閉写像の概念は一致せず,開写像だけど閉写像でないものや,逆に閉写像だけど開写像ではないものがあります。後の具体例で確認しましょう。
連続写像の定義と似ていますね。比較のため,連続写像の定義を見ておきましょう。
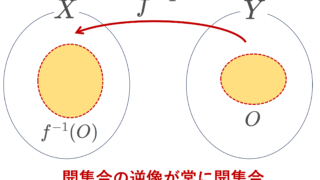
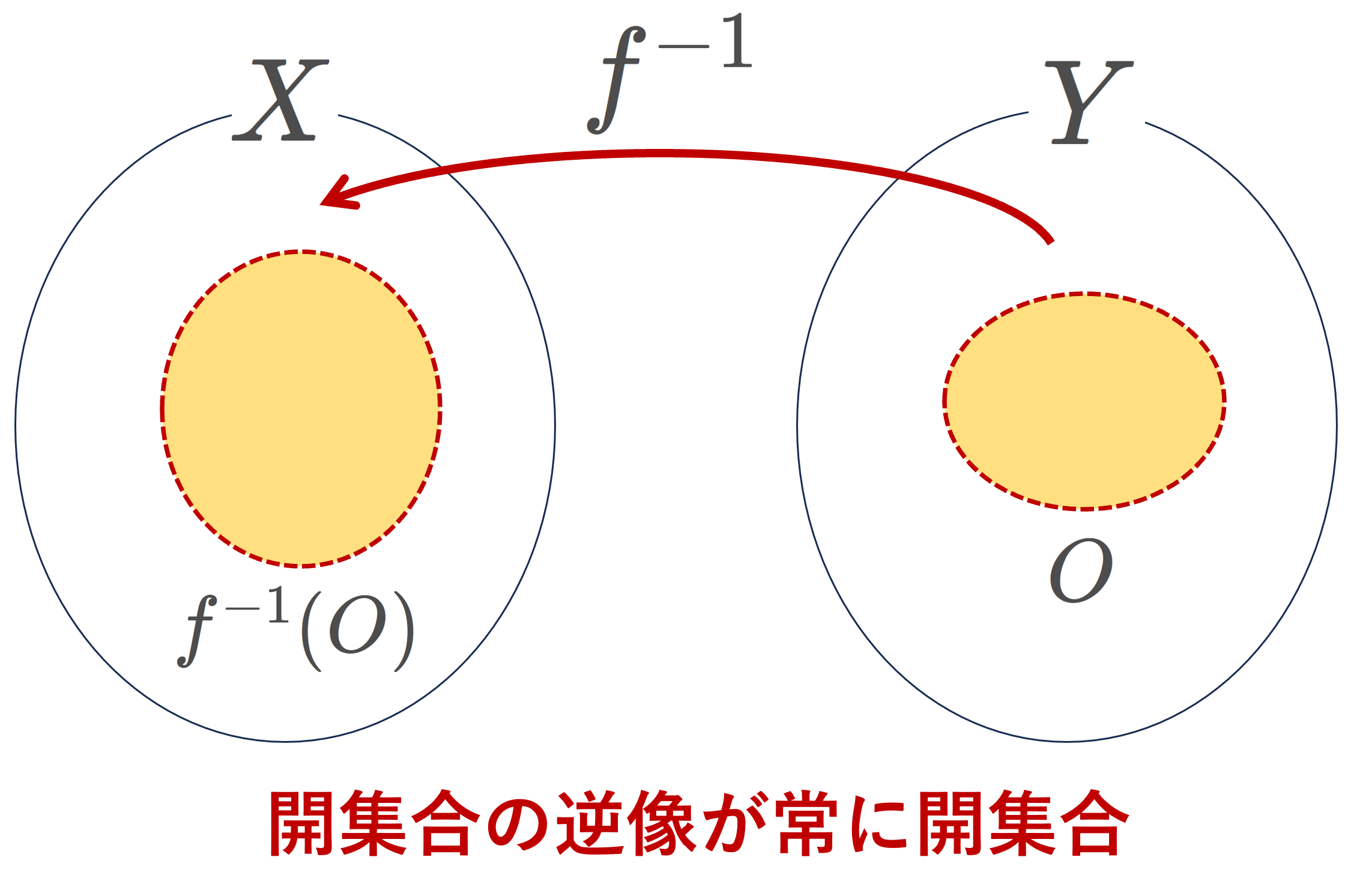
O_Y\in\mathcal{O}_Y \implies f^{-1}(O_Y)\in\mathcal{O}_X が成り立つとき, f は連続 (continuous) であるという。これは, F_Y\in\mathcal{F}_Y \implies f^{-1}(F_Y)\in\mathcal{F}_X と言っても同じである。
開集合の逆像が開集合になるものが連続写像です。これは,閉集合の逆像が閉集合になるといっても同じです。
開写像・閉写像の定義は像を使っていますが,連続写像の定義は,逆像を使っています。開写像と閉写像の概念は一致しませんが,連続写像の定義は,開集合の逆像を使っても,閉集合の逆像を使ってもかまいません。これは,写像の像・逆像と集合との演算証明からもわかるように,像より逆像の方が,集合演算の性質が良いからです。詳しくは,位相空間における連続写像の定義と性質を詳しくをみてください。
開写像・閉写像の概念は大切ですが,連続写像ほど重要ではありません。
開写像・閉写像とそうでない具体例10個
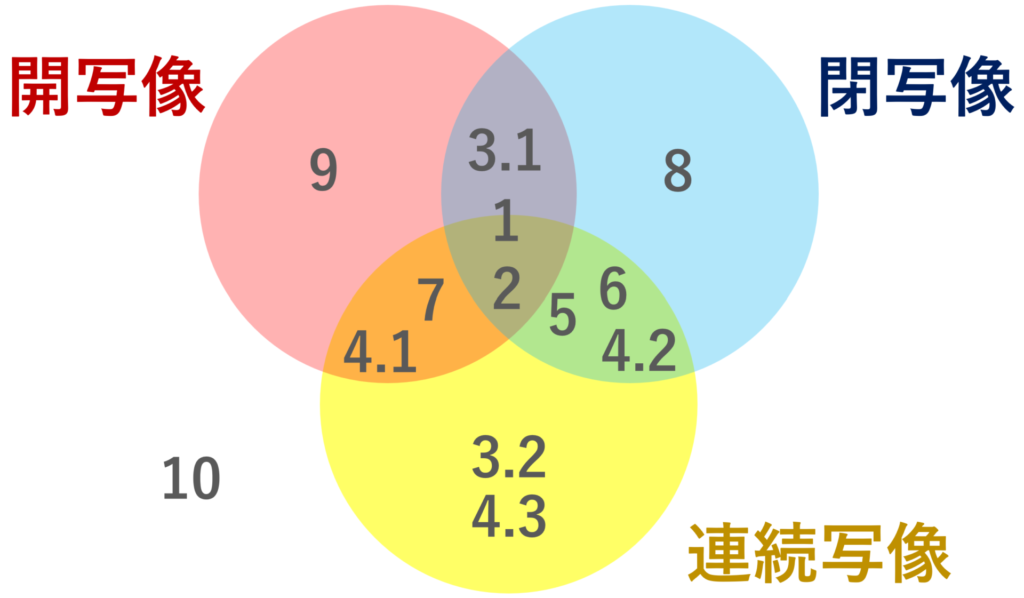
開写像・閉写像と,そうでないような写像,さらに連続性とも絡めて具体例を紹介しましょう。以下のベン図は,各具体例が開写像かどうか,閉写像かどうか,連続かどうかを表しています。数字が具体例の数字を表しています。
例1(離散空間への写像).
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y とする。
Y が離散空間であれば,任意の A\subset X に対し, f(A)\subset Y は開集合かつ閉集合です。よって言えますね。
例2(同相写像).
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y を同相写像とする。このとき, f は連続で,開かつ閉である。
同相写像は定義から当然連続であり,また, f^{-1} が連続であることと, f^{-1} における,集合の逆像が f を用いてかけることから,
A\in \mathcal{O}_X\implies f(A)\in\mathcal{O}_Y
が成り立つので,開写像です。また連続写像は,閉集合の逆像も閉集合に移すので,閉写像であることも言えます。
関連して,あとの定理3も見てください。
例3(恒等写像).
X を空でない集合とし,\mathcal{O}_1, \mathcal{O}_2 を X 上の位相とする。このとき,恒等写像 \mathrm{id}\colon (X,\mathcal{O}_1)\to (X,\mathcal{O}_2) について,
- \mathrm{id} が開写像 \iff \mathcal{O}_1\subset \mathcal{O}_2\iff\mathrm{id} が閉写像
- \mathrm{id} が連続写像 \iff \mathcal{O}_1\supset \mathcal{O}_2
\mathcal{O}_1\subsetneq\mathcal{O}_2 なら,開かつ閉だが連続でない例となり,\mathcal{O}_1\supsetneq \mathcal{O}_2 なら,連続だが開でも閉でもない例になっています。
なお,1.に関連して,f が全単射なら, f が開写像 \iff f が閉写像が言えます。あとの定理2を見てください。
例4(包含写像).
\R に通常の位相を入れ, (0,1), [0,1], [0,1) には, \R から定まる相対位相を入れる。
相対位相を入れた各空間における全体集合 (0,1), [0,1], [0, 1) は,各相対位相に関して開集合かつ閉集合です。その像 \iota_1((0,1))=(0,1),\, \iota([0,1])=[0,1],\, \iota_3([0,1))=[0,1) は, \R の位相に関して,それぞれ開集合だが閉集合でない,閉集合だが開集合でない,開集合でも閉集合でもないので,それぞれ分かります。
例5(定数関数).
f\colon \R\to \R が 定数関数 f(x)= c\; (x\in \R) であるとき, f は連続かつ閉であるが,開ではない。
1点集合 \{c\}\subset \R は閉集合ですが開集合ではありませんので,わかります。
例6.
f\colon \R\to \R が f(x)= x^2 であるとき, f は連続かつ閉であるが,開ではない。
f((-1, 1))= [0,1) は開集合でないので,開写像ではありません。閉写像であることを示しましょう。
f|_{[0,\infty)}\colon [0,\infty)\to [0,\infty) とすると,これは同相写像ですし,同様に f|_{(-\infty, 0]}\colon (-\infty, 0]\to [0,\infty) も同相写像です。 [0,\infty)=\R\setminus (-\infty,0) は閉集合であるので, A\subset \R を閉集合とするとき, A\cap (-\infty, 0] も閉集合です。同様に A\cap [0,\infty) も閉集合です。ここで,
f(A) = f|_{(-\infty, 0]} (A\cap (-\infty,0]) \cup f|_{[0,\infty)} (A\cap [0,\infty))
であり,右辺は位相空間 [0,\infty) の部分集合として,2つの閉集合の和集合なので,[0,\infty) 上の閉集合です。 [0,\infty) 上の閉集合は \R 上でも閉集合なので, f(A) が閉集合であることが分かりました。
注意ですが, f\colon \R\to [0,\infty) とみると,[0,1) も開集合になるため, f は開写像となります。終域をどうするかは重要です。
例7(射影).
f\colon \R^2\to \R を, f(x,y)=x とするとき, f は連続かつ開であるが,閉ではない。
C = \{ (x, 1/x)\mid x\ne 0\} とすると, C\subset \R^2 は閉集合ですが, f(C)=\R\setminus\{0\} は閉集合ではないので, f は閉写像ではありません。
開写像であることを示しましょう。 A\subset \R^2 を開集合としましょう。このとき,任意の (a,b)\in A に対し,
(a,b)\in (a-\varepsilon, a+\varepsilon)\times (b-\varepsilon , b+\varepsilon )\subset A
となる \varepsilon>0 が取れます。このとき,真ん中の集合の f による像は, (a-\varepsilon, a+\varepsilon) ですから,
です。任意の (a,b)\in A に対し,その像 f(a,b) が f(A) の内点になることが分かったので, f(A) は開集合ですね。よって,開写像であることが示せました。
なお一般に,直積空間から,各空間への射影は常に開写像になります。
例8(ディリクレ関数).
f\colon \R\to\R を f(x)=\begin{cases} 1 & x\in \mathbb{Q},\\ 0& x\in \R \setminus \mathbb{Q}\end{cases} とすると, f は閉であるが,開でも連続でもない。
f の像は \emptyset, \{0\},\{1\}, \{0,1\} のいずれかで,これは全て閉集合なので, f は閉写像です。一方, f((2,3))=\{0,1\} は開集合ではないので,開写像ではありません。
例9(ディリクレ関数2).
\R における通常の位相を \mathcal{O} とし,0 を含む部分集合を開集合族とする位相を
\mathcal{O}_0=\{ U\subset \R\mid 0\in U\}
とする。 f\colon (\R,\mathcal{O})\to(\R,\mathcal{O}_0) を f(x)=\begin{cases} 1 & x\in \mathbb{Q},\\ 0& x\in \R \setminus \mathbb{Q}\end{cases} とすると, f は開であるが,閉でも連続でもない。
任意の \mathcal{O}-開集合 A\subset \R に対し, 0\in f(A) なので, f(A) は\mathcal{O}_0-開集合です。一方で,集合 f(\{0\})=\{0\} は \mathcal{O}_0-閉集合ではありません。また,f^{-1}(\{0\})=\{0\} \cup(\R\setminus \mathbb{Q}) は \mathcal{O}-開集合ではないので,連続ではありません。
例10.
f\colon \R\to\R を f(x)=\begin{cases} x & x\in \mathbb{Q},\\ 0& x\in \R \setminus \mathbb{Q}\end{cases} とすると, f は開でも閉でも連続でもない。
f((1,2)) = ((1,2)\cap\mathbb{Q})\cup\{0\} は開集合ではありませんし, f([0,1])=[0,1]\cap \mathbb{Q} は閉集合ではありません。
開写像・閉写像の性質4つ
定理1(開写像・閉写像の同値な性質)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y とする。このとき,
- f が開写像 \iff \forall A\subset X, \, f(\operatorname{Int}(A))\subset \operatorname{Int}(f(A))
- f が閉写像 \iff \forall A\subset X, \, \overline{f(A)}\subset f(\overline{A})
\operatorname{Int} は内部(開核)の意味で, \overline{\hspace{4pt}\cdot\hspace{4pt}} は閉包の意味です。 X, Y どっちの空間における内部(開核)・閉包なのかが,左辺と右辺で違いますので注意が必要です。
ちなみに, f が連続 \iff \forall A\subset X, \,f(\overline{A})\subset\overline{ f(A)} が知られています(→位相空間における連続写像の定義と性質を詳しく)。閉写像のときと包含関係が逆ですね。
証明
1.について
f が開写像ならば,任意の A\subset X に対し, f(\operatorname{Int}(A)) は開集合になる。これと f(\operatorname{Int}(A))\subset f(A) であることより, f(\operatorname{Int}(A))\subset \operatorname{Int}(f(A)) がわかる。
逆に,任意の A\subset X で f(\operatorname{Int}(A))\subset \operatorname{Int}(f(A)) とする。 A を開集合とすると, f(A)\subset \operatorname{Int}(f(A)) となるので, f(A) は開集合である。よって, f は開写像である。
2.について
f が閉写像ならば,任意の A\subset X に対し, f(\overline{A}) は閉集合になる。これと f(A)\subset f(\overline{A}) であることより, \overline{f(A)}\subset f(\overline{A}) がわかる。
逆に,任意の A\subset X で \overline{f(A)}\subset f(\overline{A}) とする。 A を閉集合とすると, \overline{f(A)}\subset f(A) となるので, f(A) は閉集合である。よって, f は閉写像である。
証明終
定理2(全単射なら開写像 \iff 閉写像)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y とする。
f が全単射ならば,開写像であることと閉写像であることは同値である。
証明
A\subset X とする。 f が単射であることと,全射であることを順番に適用することで,
f(X\setminus A)=f(X)\setminus f(A)=Y\setminus f(A)
となる(→写像の像・逆像と集合との演算証明)。開集合の補集合は閉集合で,閉集合の補集合は開集合であることに注意する。
f が開写像のときは, A\subset X を任意の閉集合とすることで, f が閉写像であることが示せる。 f が閉写像のときは, A\subset X を任意の開集合とすることで, f が開写像であることを示せる。
証明終
定理3(同相写像と開写像・閉写像)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とし, f\colon X\to Y を全単射かつ連続とする。このとき,以下の3つは同値である。
証明
1.\iff 2.について
f^{-1} における,集合の逆像は f を用いてかけることに注意する。
U\in\mathcal{O}_X\implies f(U)\in \mathcal{O}_Y
とは,f^{-1} が連続であることの定義であるし, f が開写像である定義でもある。よって,1.\iff2.である。
2. \iff3.については,定理2で示した。
証明終
定理4(開写像・閉写像と合成)
(X,\mathcal{O}_X), (Y, \mathcal{O}_Y),(Z,\mathcal{O}_Z) を位相空間とし, f\colon X\to Y,g\colon Y\to Z とする。このとき,その合成 g\circ f\colon X\to Z について,
- f,g がともに開写像なら, g\circ f も開写像である
- f,g がともに閉写像なら, g\circ f も閉写像である
なお, f,g がともに連続写像なら,その合成 g\circ f も連続写像になります(→位相空間における連続写像の定義と性質を詳しく)
証明
1.について
A\in\mathcal{O}_X とすると, f は開写像より, f(A)\in \mathcal{O}_Y である。これと g は開写像より, g(f(A))\in\mathcal{O}_Z となるから, g\circ f は開写像である。
2.についても,1.と同様である。
証明終