正方行列に対して定義されるトレース（跡）とは，対角成分の和を指します。これについて，定義を整理し，その性質をいくつか証明しましょう。
行列のトレース(tr)の定義
定義（行列のトレース）
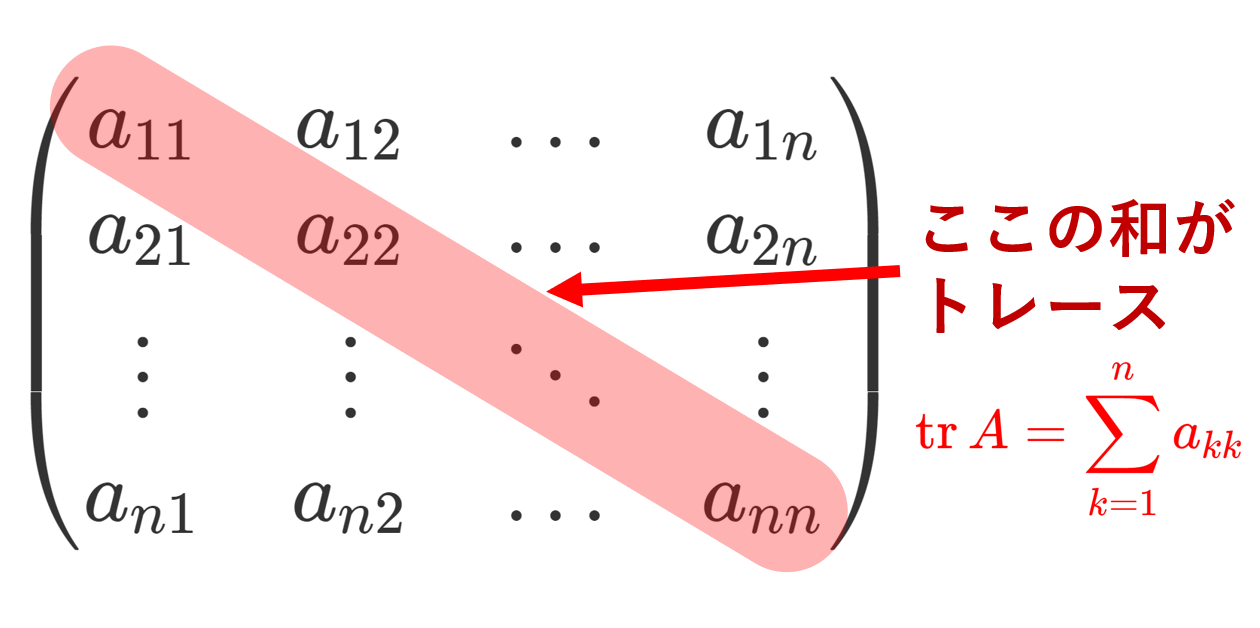
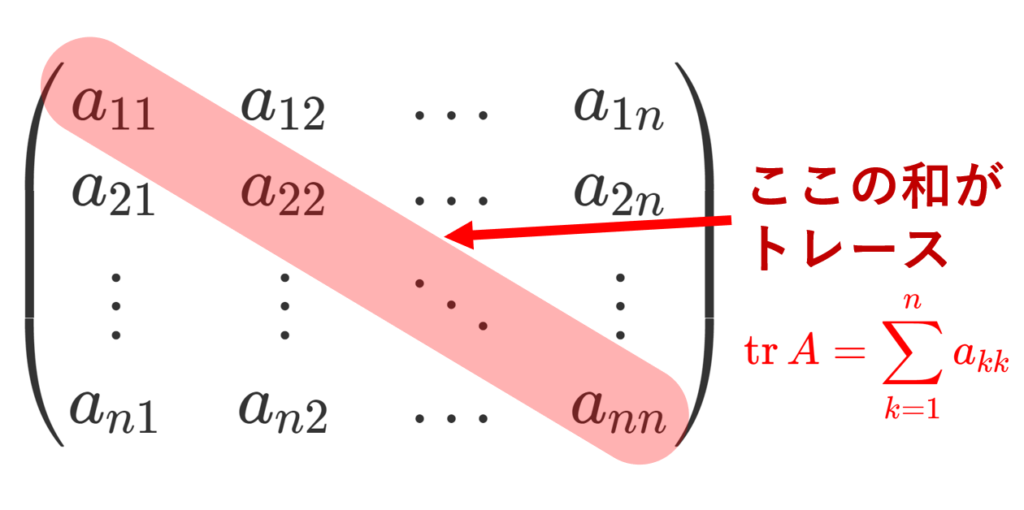
A = (a_{ij}) を n 次正方行列とする。このとき，対角成分の和
\color{red} \operatorname{tr} A = \sum_{k=1}^n a_{kk}
を行列のトレース (trace, 跡) という。
行列のトレース(tr)の性質
行列のトレースの性質について
- 基本的な性質
- 可換不変性と相似不変性
- 固有値との関係
- 可換性をみたす線形汎関数はトレースに限る
の順に紹介しましょう。
トレースの基本的な性質
定理（トレースの基本的な性質）
A,B を n 次正方行列とする。このとき，
これは，どれもトレースの定義から明らかなので省略します。
トレースの可換不変性と相似不変性
定理（トレースの可換・相似不変性）
証明してみましょう。
証明
\operatorname{tr} (AB) = \operatorname{tr} (BA) について
A=(a_{ij}), B=(b_{ij}) とすると，
\begin{aligned} \operatorname{tr} (AB) &= \sum_{k=1}^n (AB)_{kk} \\ &= \sum_{k=1}^n \sum_{l=1}^m a_{kl} b_{lk} \\ &= \sum_{l=1}^m \sum_{k=1}^n b_{lk} a_{kl} \\ &= \sum_{l=1}^m (BA)_{ll} \\ &= \operatorname{tr} (BA) \end{aligned}
より従う。
\operatorname{tr} (P^{-1}AP) = \operatorname{tr} A について
上より， \operatorname{tr} ((P^{-1}A)P) = \operatorname{tr} (P(P^{-1}A)) = \operatorname{tr} A となって従う。
証明終
トレースは固有値の和に一致
定理（トレースと固有値の和）
A を n 次正方行列， \lambda_1,\lambda_2,\dots , \lambda_n をその固有値とすると，
\operatorname{tr} A = \sum_{k=1}^n \lambda_k.証明
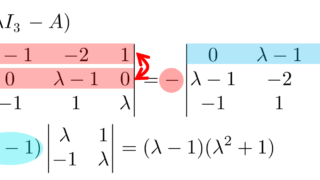
固有多項式の根が \lambda_1,\lambda_2,\dots , \lambda_n であるのと，両辺の x^n の係数の比較により，
\small \det (xE_n - A ) = (x-\lambda_1)(x-\lambda_2)\dots (x-\lambda_n)
が成立する。両辺の x^{n-1} の係数を比較することで，
が分かる。
証明終
可換性がある線形汎関数はトレースに限る
定理
f\colon M_n(\mathbb{C} ) \to \mathbb{C} が
- f(\alpha A+\beta B) = \alpha f(A)+\beta f(B) \,\,(\alpha, \beta\in \mathbb{C}) (線形性)
- f(AB) = f(BA) (可換性)
をみたすとき， f(A) =c\operatorname{tr} A \,\, (c\in\mathbb{C}) (トレースの定数倍)とかける。
ここで， \color{red}M_n(\mathbb{C} ) は各成分が複素数である n 次正方行列全体の集合を指します。
なお，本定理は \mathbb{C} を \mathbb{R} に変えても成立します。
証明
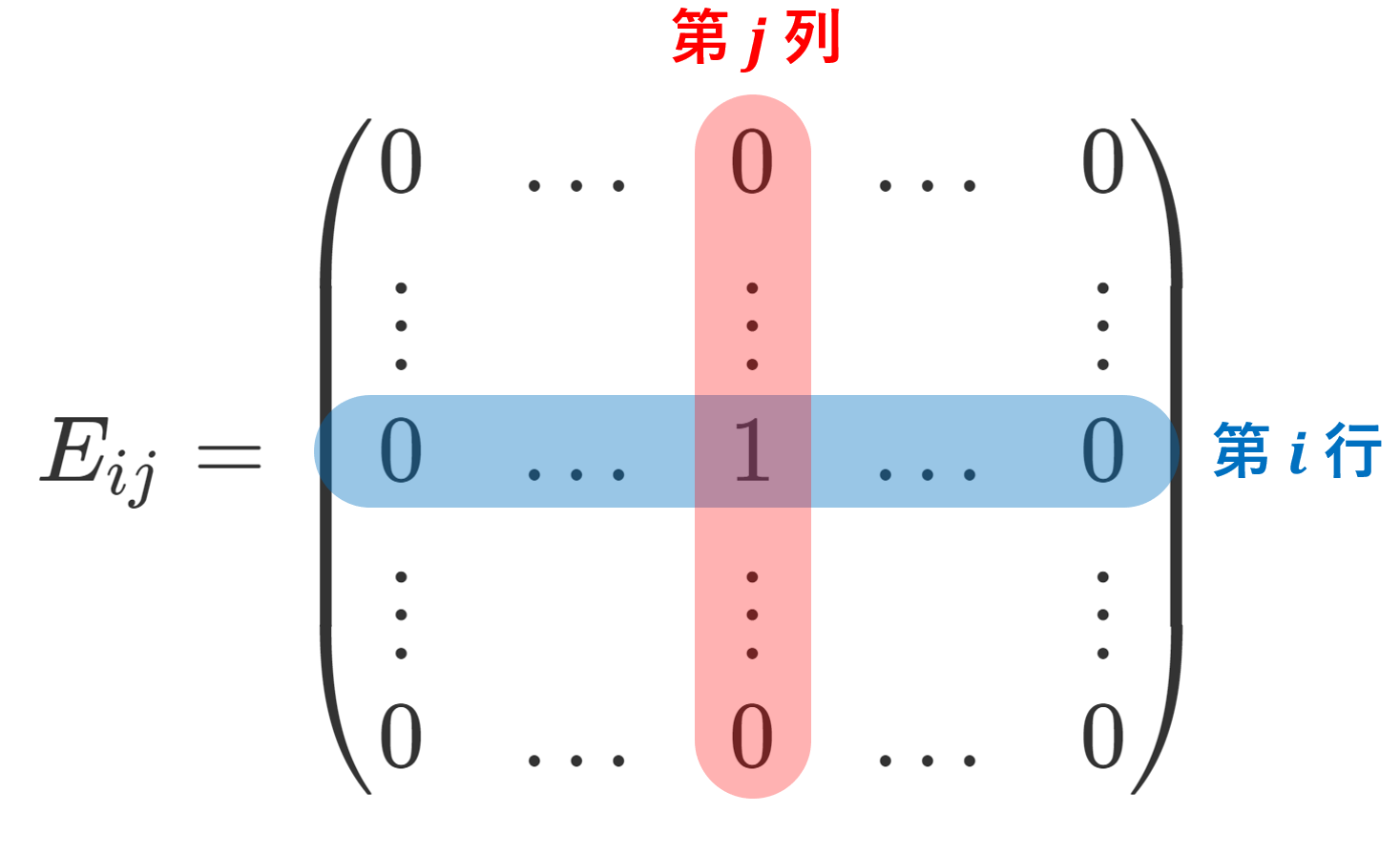
(i,j) 成分のみが 1 でそれ以外の成分が 0 である n 次正方行列を E_{ij} と書くことにする(行列単位という→行列単位とは～定義と性質～)。
f(E_{ij} ) = c_{ij} とおくと，線形性より f(A) = \sum_{i,j} c_{ij}a_{ij} とかける。
ここで，一般に E_{ij} E_{kl} =\delta_{jk} E_{il} であることに注意する。ただし， \delta_{jk} はクロネッカーのデルタを表す。
f の可換性から，
がわかる。 j=k とすることで c_{il} = \delta_{li} c_{kk} となり，特に i \ne j のとき c_{il} = 0 ， i=l のとき， c_{ll} = c_{kk} となる。
以上から， c_{ij} = 0 \,\,(i\ne j ) と c_{11} = c_{22} = \dots = c_{nn} がわかるから，後半の等式の値を c とおくと，
f(A) = \sum_{k=1}^n c a_{kk} =c \operatorname{tr} A
を得る。
証明終
