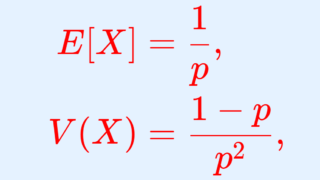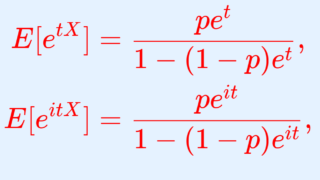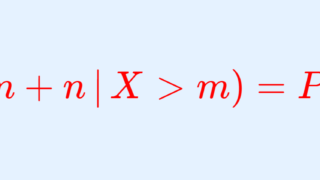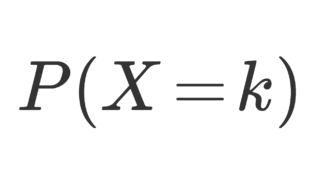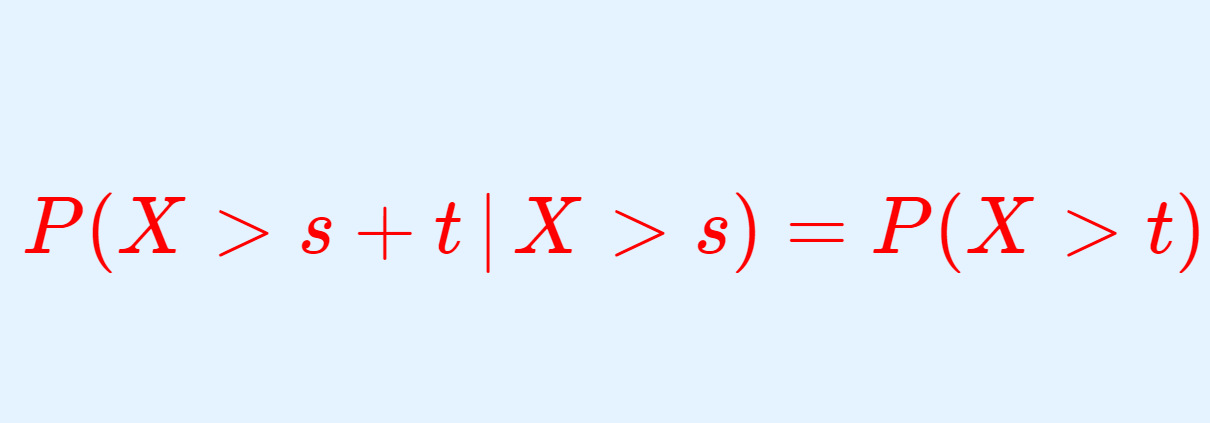幾何分布とは,確率 p で表が出るコインを何回も投げたときに,初めて表が出るのは何回目になるかの分布を表す,離散型確率変数です。これについて,その定義と性質を掘り下げていきましょう。
幾何分布の定義
定義(幾何分布)
X を確率変数, 0<p<1 とする。 k=1,2,3,\ldots に対し,
\color{red} P(X=k) = (1-p)^{k-1} p
が成立するとき, X はパラメータ p の幾何分布 (geometric distribution) に従うという。本記事では,これを \color{red} X\sim \operatorname{Geo}(p) とかくことにする。
幾何分布は,確率 p で表が出るコインを投げたときに,初めて表が出るのは何回目かを表す分布といえます。

実際,k 回目に初めて表が出る確率は,最初の k-1 回は 1-p の確率で起こる「裏」が出続けて,最後の 1 回に,確率 p の確率で起こる「表」が出るため,確率は (1-p)^{k-1} p になりますね。
たとえば,サイコロを複数回振ったとき, X 回目に初めて1の目が出るとすると, X \sim \operatorname{Geo}(1/6) となります。
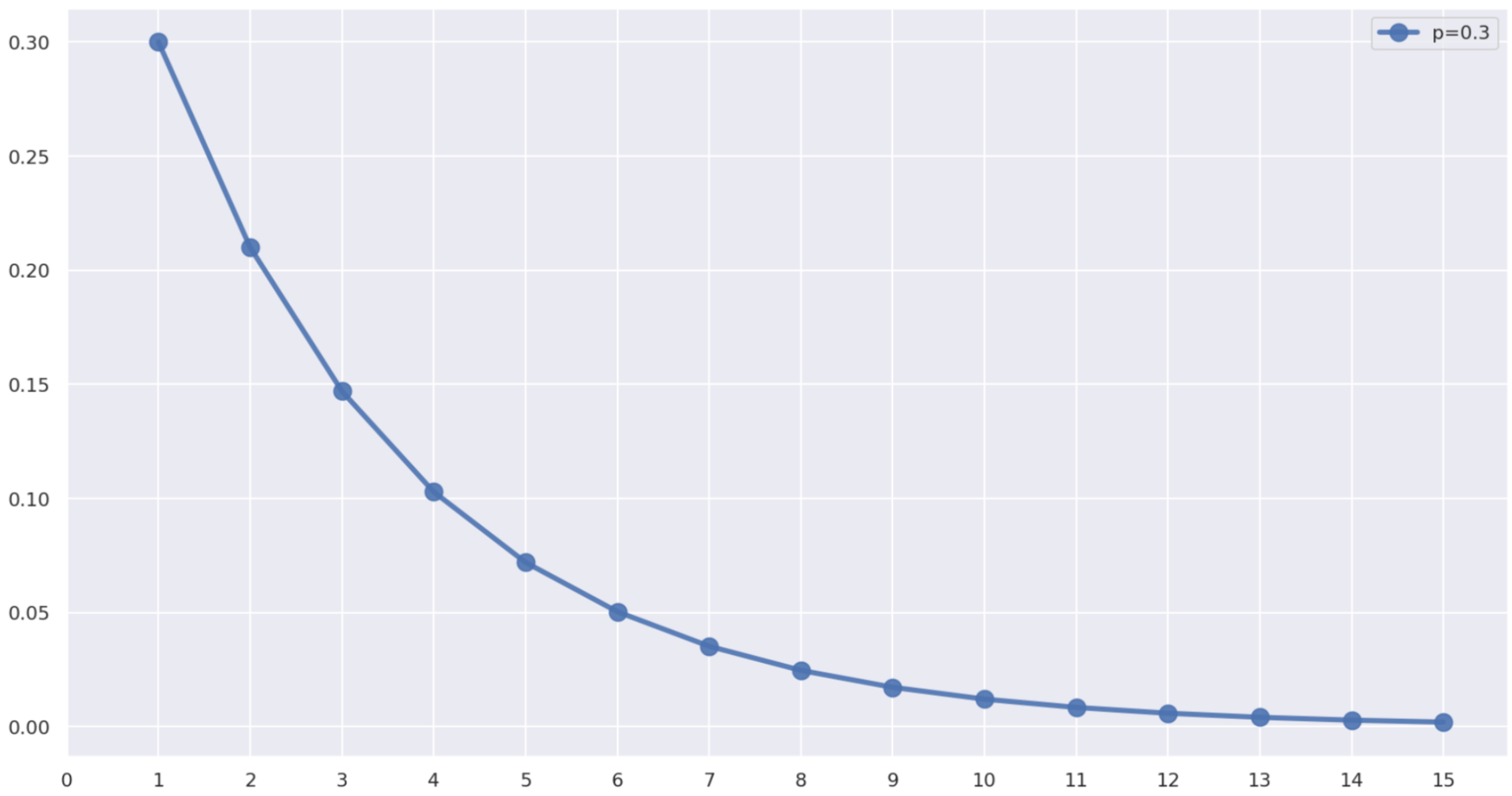
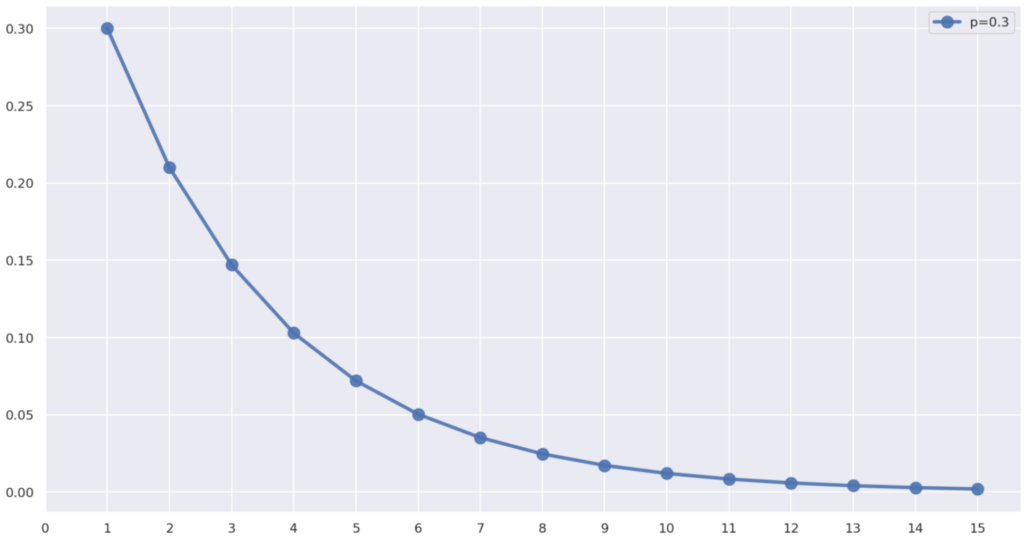
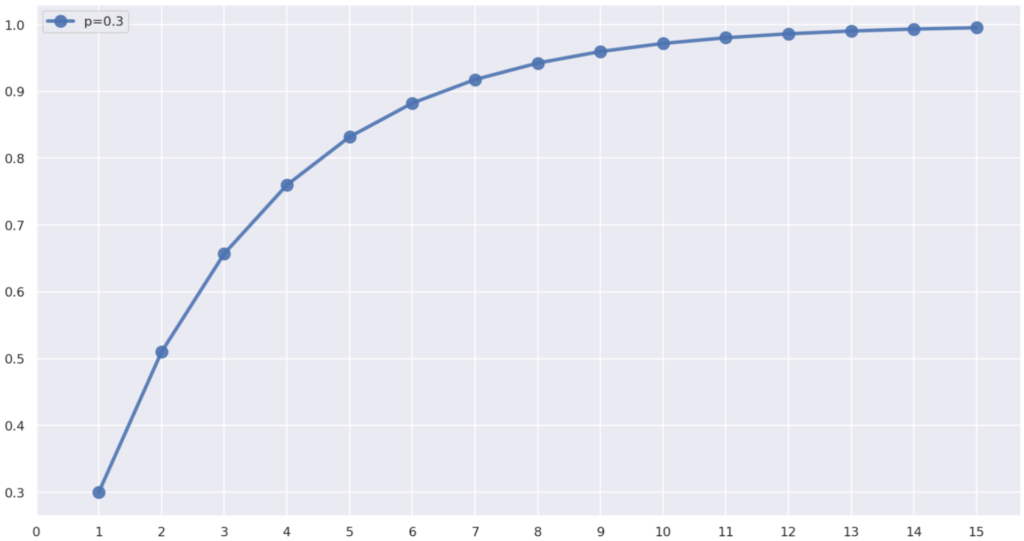
p=0.3 のときの P(X=k) を図示すると,以下のようになります。
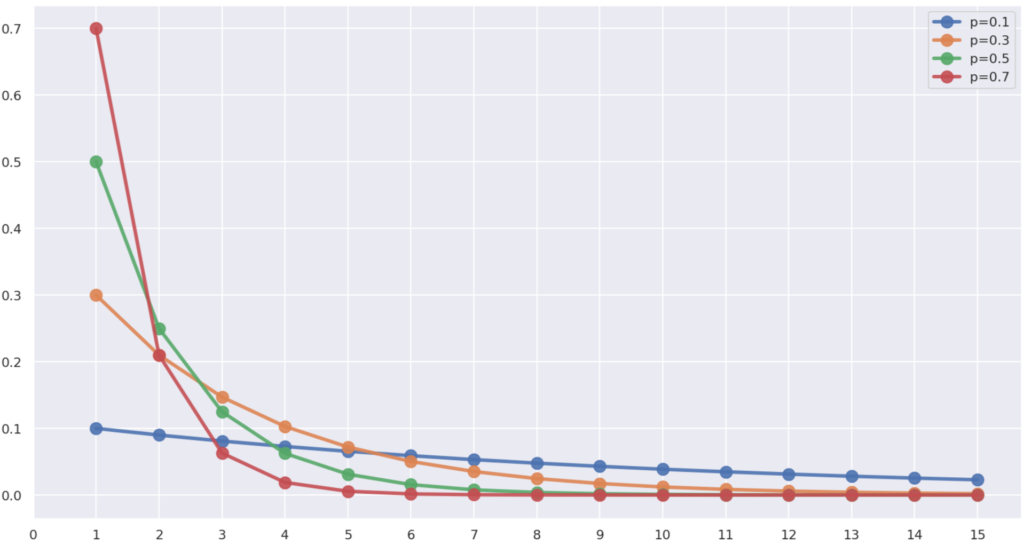
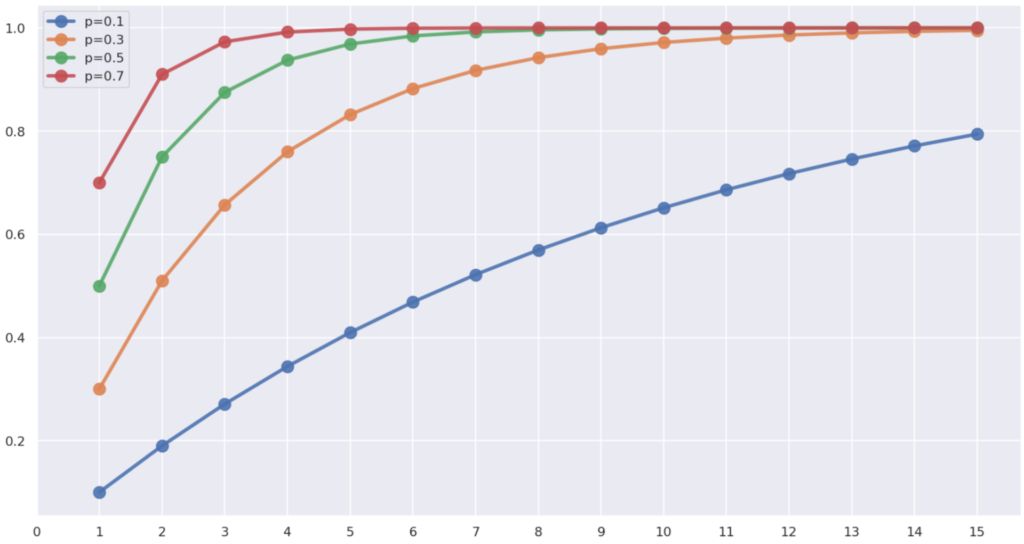
また, \color{red} p=0.1, 0.3, 0.5, 0.7 と変えたときの,確率の P(X=k) の違いは,以下のようになります。
幾何分布の性質まとめ
幾何分布の性質を列挙しましょう。
| 性質 | 幾何分布 \operatorname{ Geo}(p) |
|---|---|
| 確率 | P(X=k) = (1-p)^{k-1} p \,\;(k=1,2,3,\ldots) |
| 確率の型 | 離散型 |
| 累積分布関数 F(x) = P(X\le x) | \begin{cases} 0 & x<1 , \\ 1-(1-p)^{\lfloor x \rfloor} & x\ge 1 \end{cases} |
| ベルヌーイ分布との関係 | \inf\{ n\mid X_n = 1\} |
| 期待値(平均) E[X] | \dfrac{1}{p} |
| 分散 V(X) | \dfrac{1-p}{p^2 } |
| 標準偏差 \sqrt{V(X)} | \dfrac{\sqrt{1-p}}{p} |
| 積率母関数(モーメント母関数) E[e^{tX}] | \dfrac{pe^{t}}{1-(1-p)e^t}, \;\; t< -\log(1-p) |
| 特性関数 E[e^{itX}] | \dfrac{pe^{it}}{1-(1-p)e^{it}} |
| 無記憶性 | P(X>m+n\,|\, X>m ) =P(X>n) |
以上について,累積分布関数以降を,順番に紹介していきましょう。
幾何分布の累積分布関数(分布関数)
幾何分布の累積分布関数(分布関数)は,
\begin{aligned}P(X\le x) &= \sum_{k\le x} P(X=k) \\ &= \begin{cases} 0 & x < 1, \\ \sum_{k=1}^{\lfloor x \rfloor} (1-p)^{k-1} p & x \ge 1\end{cases} \\ &= \begin{cases} 0 & x< 1, \\ \frac{1-(1-p)^{\lfloor x \rfloor}}{1-(1-p)}p & x\ge 1 \end{cases} \\ &= \begin{cases} 0 & x<1 , \\ 1-(1-p)^{\lfloor x \rfloor} & x\ge 1 \end{cases} \end{aligned}
となります。 p=0.3 のときの累積分布関数をグラフで描くと,以下のようになります。(※ 以下は模式的なもので,実際のグラフは床関数(ガウス記号)のグラフのように,不連続な関数になります)
また, \color{red} p=0.1, 0.3, 0.5, 0.7 と変えたときの,累積分布関数の違いは,以下のようになります。
p が大きいほど,グラフが「上」になりますね。
幾何分布のベルヌーイ分布との関係
幾何分布は「確率 p で表が出るコインにおいて,初めて表が出る試行回数」と思えるのでした。
一方,ベルヌーイ分布は「確率 p で表が出るコインを一回投げたときに,表が出るかどうか」をモデル化したものであり, Y をパラメータ p のベルヌーイ分布に従う確率変数とすると, P(Y=1)=p, \,\, P(Y=0) = 1-p でした。
よって,幾何分布は,独立な,パラメータ p のベルヌーイ分布に従う確率変数 X_1, X_2, \ldots において, X_1=X_2=\dots = X_{n-1}=0,\, X_n=1 となるときの n の値だということができますね。したがって,
\color{red} X \stackrel{\mathrm{d}}{=}\inf\{ n\mid X_n = 1\}
が成り立つわけです。(ただし, \stackrel{\mathrm{d}}{=} は分布の意味で等しいことを意味します。)
幾何分布の期待値(平均)・分散・標準偏差
定理(幾何分布の期待値(平均)・分散・標準偏差)
X \sim \operatorname{Geo}(p) とする。このとき, X の期待値・分散・標準偏差はそれぞれ
\color{red} \begin{aligned}E[X] &= \dfrac{1}{p}, \\ V(X)&= \dfrac{1-p}{p^2 }, \\ \sqrt{V(X)} &= \dfrac{\sqrt{1-p}}{p} \end{aligned}
である。
これの証明は,以下の記事で与えています。
幾何分布の積率母関数・特性関数
定理(幾何分布の積率母関数・特性関数)
X \sim \operatorname{Geo}(p) とする。このとき,幾何分布の積率母関数(モーメント母関数)・特性関数はそれぞれ
\color{red}\begin{aligned} E[e^{tX}] &=\dfrac{pe^{t}}{1-(1-p)e^t}, \quad t< -\log(1-p), \\ E[e^{itX}]&= \dfrac{pe^{it}}{1-(1-p)e^{it}}, \quad t\in\mathbb{R} \end{aligned}
である。
積率母関数・特性関数は,それぞれラプラス変換・フーリエ変換に対応しています。証明は,以下の記事で行っています。
幾何分布の無記憶性
幾何分布には「無記憶性」と呼ばれる,以下の性質があります。
定理(幾何分布の無記憶性)
X \sim \operatorname{Geo}(p) とし, n,m \ge 1 を正の整数とする。このとき,
\color{red}P(X>m+n\,|\, X>m ) =P(X>n)
である。これを無記憶性 (lack of memory property, memorylessness) という。
逆に,無記憶性をもつ離散型の確率分布は幾何分布に限る。
「無記憶性」とは,以前までの結果が後の結果に影響を与えないことを指します。幾何分布は,「コインで初めて表が出るまでにコインを投げる回数」をモデル化したものでしたが,たとえば, k 回目「裏」だったからと言って, k+1 回目に「表」になる確率が上がるわけではありませんね。それまでの試行は,以降の試行に関係ないわけです。
また逆に,無記憶性をもつ離散型確率分布は幾何分布に限るわけですから,離散型の確率分布で,無記憶性をもつものをモデル化したいときは,幾何分布が最適だということにもなります。
これについて詳しくは,以下の記事を参照してください。
なお,連続型確率変数においては,指数分布のみが無記憶性をもつことが知られています。これについては,指数分布の無記憶性とその証明を参照してください。