 線形代数学
線形代数学 交代行列の定義と重要な性質5つ
交代行列 (反対称行列,歪対称行列,alternating matrix) とは,転置行列が元の行列の-1倍になる行列,すなわちA^T =-Aをみたす行列を指します。
 線形代数学
線形代数学 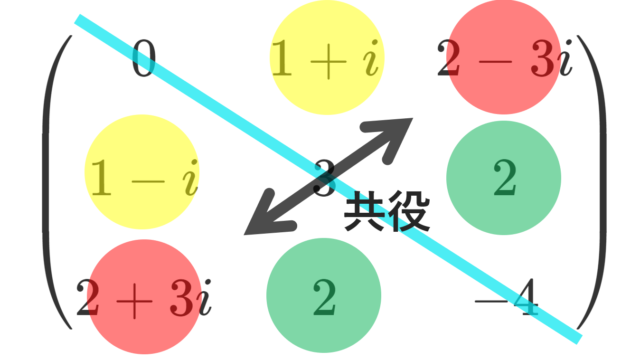 線形代数学
線形代数学 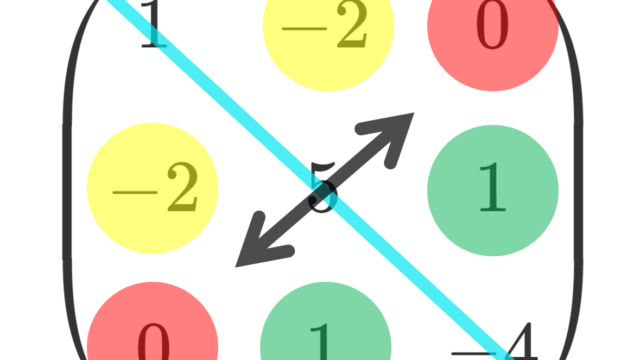 線形代数学
線形代数学  線形代数学
線形代数学 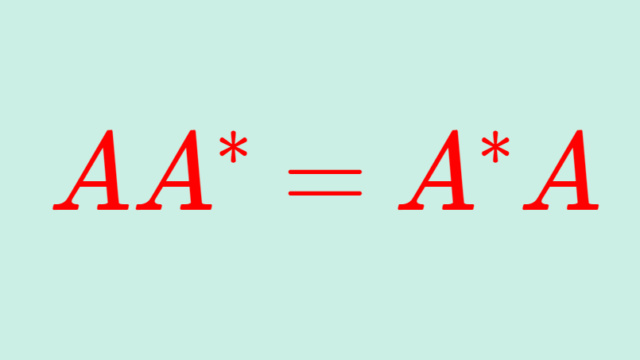 線形代数学
線形代数学 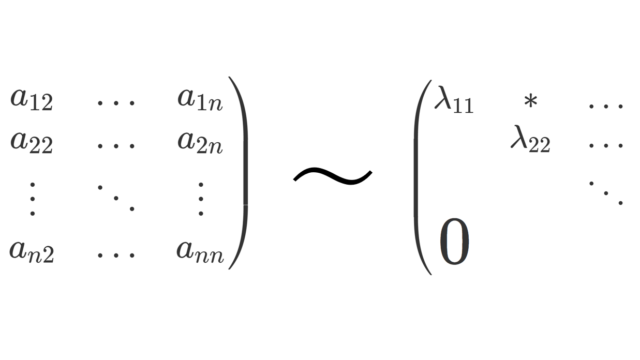 線形代数学
線形代数学 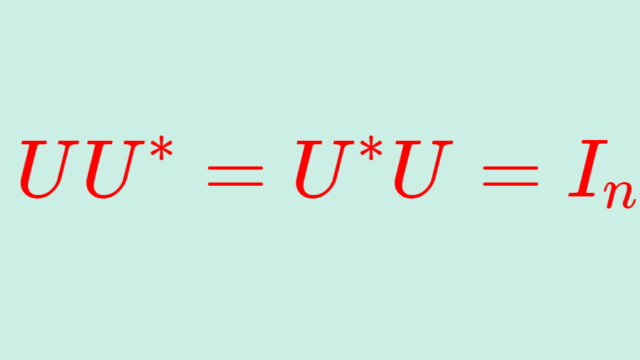 線形代数学
線形代数学 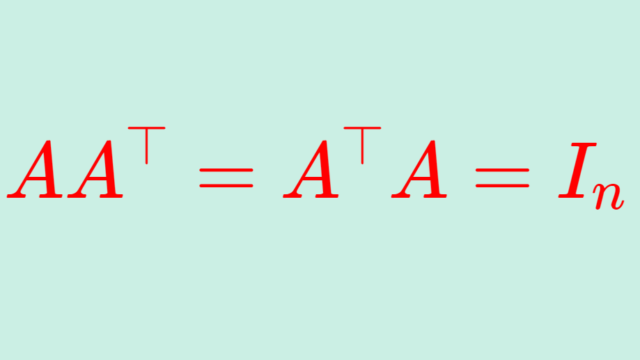 線形代数学
線形代数学 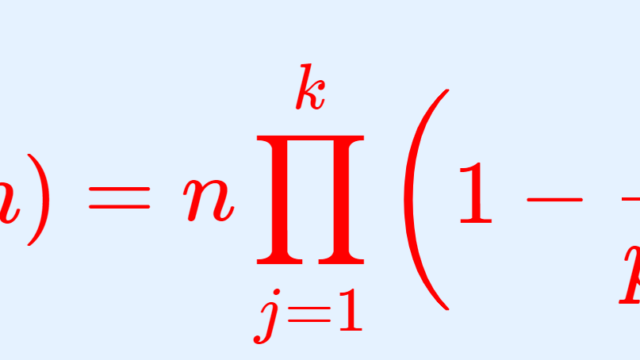 数論
数論 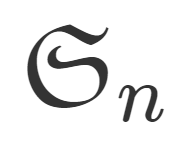 群・環・体
群・環・体