 微分積分学(大学)
微分積分学(大学) 条件収束級数は和の順序交換により任意の値に収束できることの証明
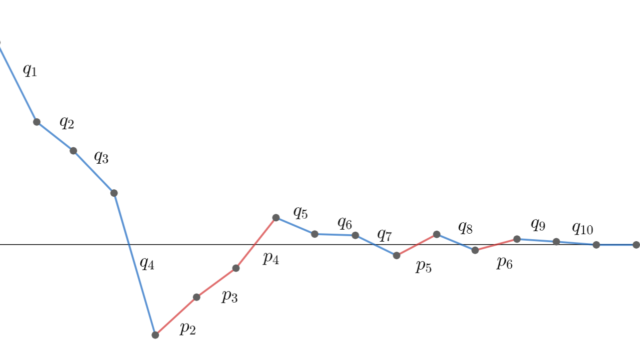
有限和においては,和の順序を交換しても同じ値に収束します。一方でこれは無限和では成立しません。単に成立しないどころか,「和の順序を変えることで任意の値に収束できる」ことがあります。今回はこのような定理を紹介・証明します。
 微分積分学(大学)
微分積分学(大学) 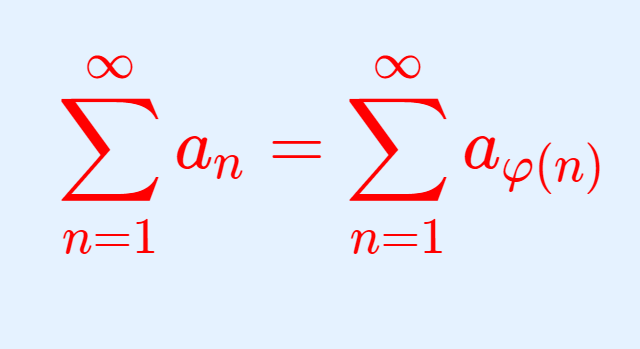 微分積分学(大学)
微分積分学(大学) 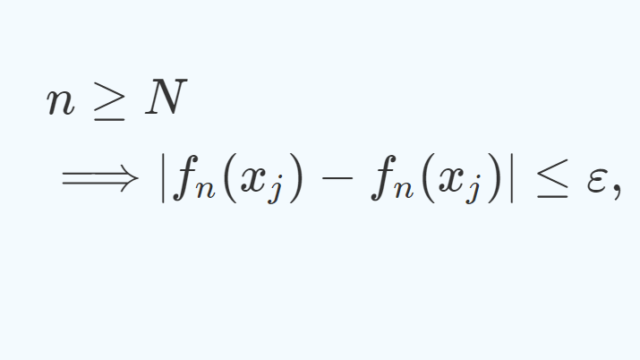 微分積分学(大学)
微分積分学(大学) 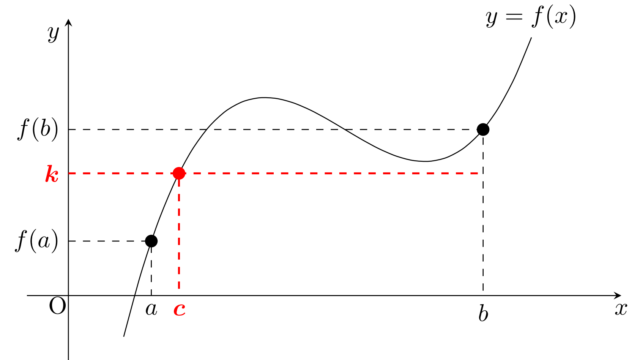 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学) 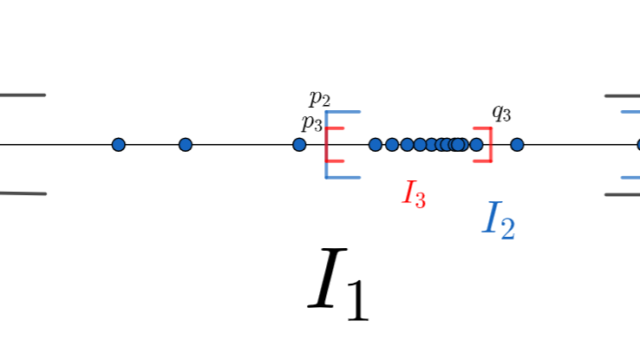 微分積分学(大学)
微分積分学(大学) 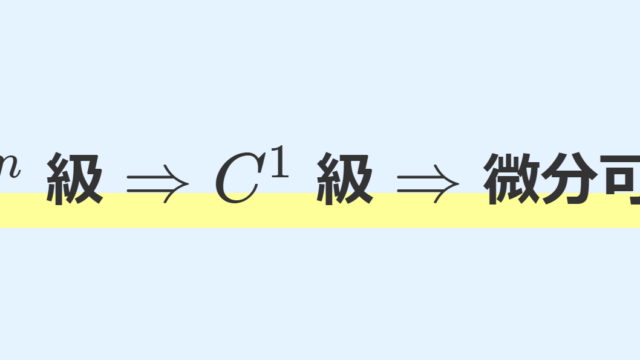 微分積分学(大学)
微分積分学(大学) 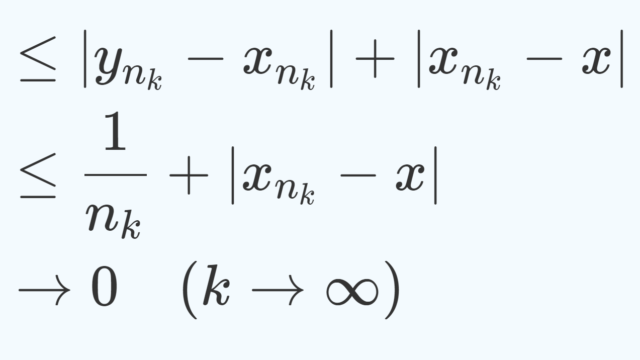 微分積分学(大学)
微分積分学(大学) 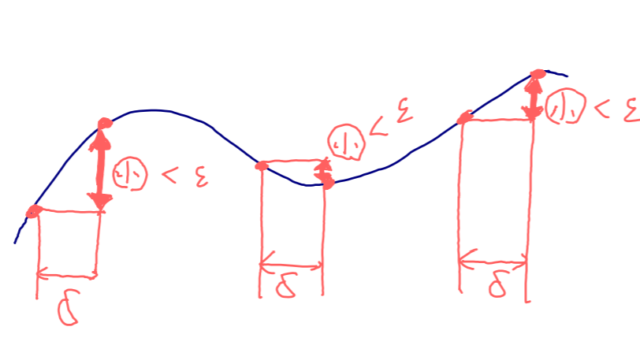 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)