 測度論
測度論 【数学科向け】ルベーグ積分の定義を段階を踏んで解説する
数学科向けに,ルベーグ積分の定義を「非負単関数→非負可測関数→一般の可測関数」の順に述べていきましょう。本記事は「お気持ち」記事ではなく,ルベーグ積分を厳密に定義していきます。測度空間・単関数・可測関数などはある程度既知とします。
 測度論
測度論  統計学
統計学  統計学
統計学 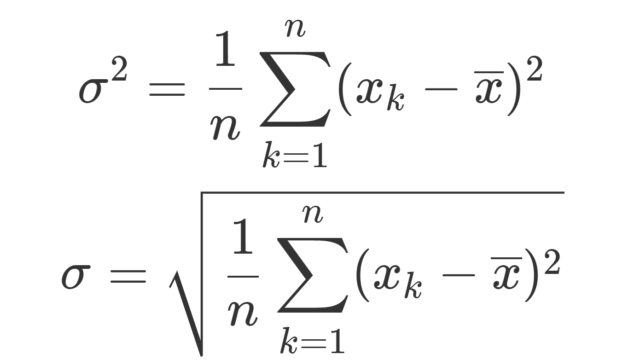 統計学
統計学 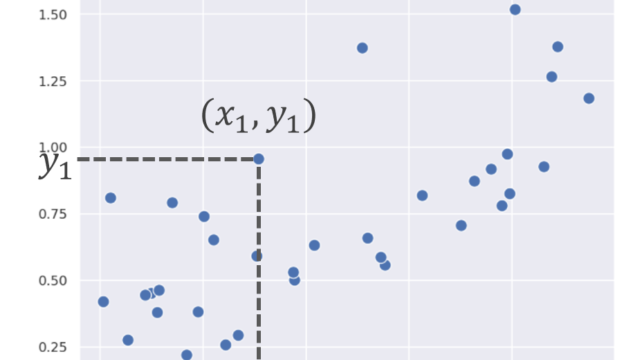 統計学
統計学 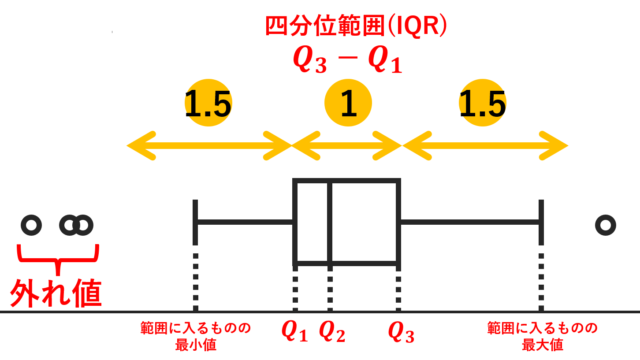 統計学
統計学 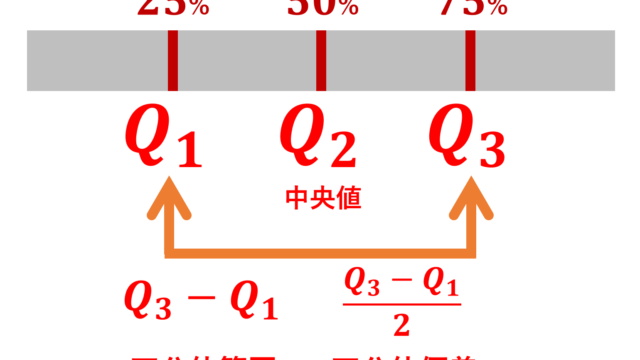 統計学
統計学 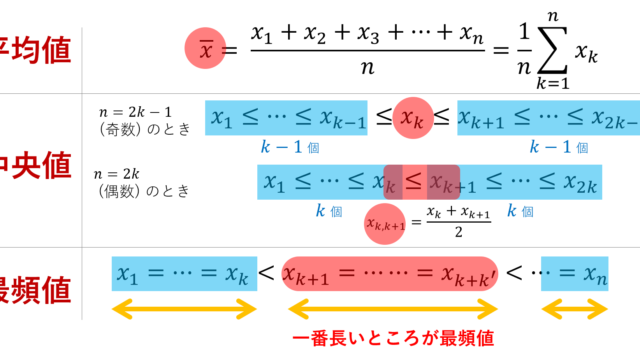 統計学
統計学 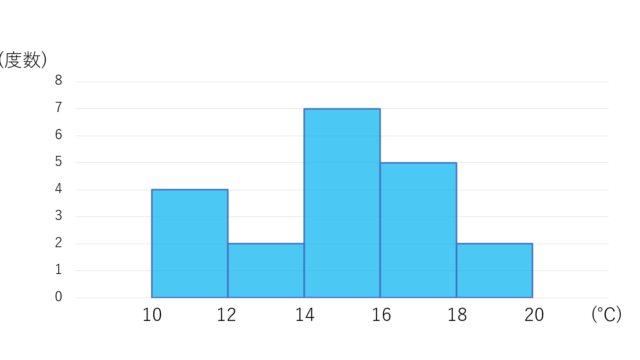 統計学
統計学 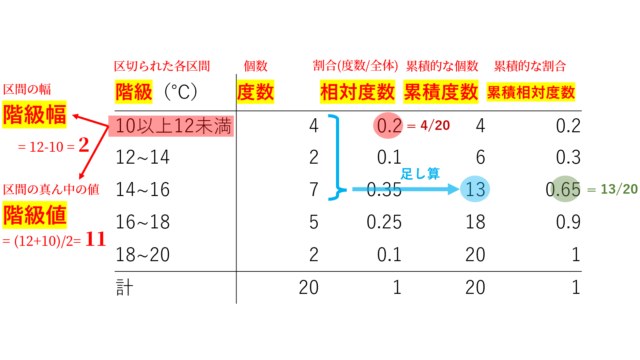 統計学
統計学